Can You Count to Nine? A Human Evaluation Benchmark for Counting Limits in Modern Text-to-Video Models

Generative models have driven significant progress in a variety of AI tasks, including text-to-video generation, where models like Video LDM and Stable Video Diffusion can produce realistic, movie-level videos from textual instructions. Despite these advances, current text-to-video models still face fundamental challenges in reliably following human commands, particularly in adhering to simple numerical constraints. In this work, we present T2VCountBench, a specialized benchmark aiming at evaluating the counting capability of SOTA text-to-video models as of 2025. Our benchmark employs rigorous human evaluations to measure the number of generated objects and covers a diverse range of generators, covering both open-source and commercial models. Extensive experiments reveal that all existing models struggle with basic numerical tasks, almost always failing to generate videos with an object count of 9 or fewer. Furthermore, our comprehensive ablation studies explore how factors like video style, temporal dynamics, and multilingual inputs may influence counting performance. We also explore prompt refinement techniques and demonstrate that decomposing the task into smaller subtasks does not easily alleviate these limitations. Our findings highlight important challenges in current text-to-video generation and provide insights for future research aimed at improving adherence to basic numerical constraints.

Exploring the Limits of KV Cache Compression in Visual Autoregressive Transformers

A fundamental challenge in Visual Autoregressive models is the substantial memory overhead required during inference to store previously generated representations. Despite various attempts to mitigate this issue through compression techniques, prior works have not explicitly formalized the problem of KV-cache compression in this context. In this work, we take the first step in formally defining the KV-cache compression problem for Visual Autoregressive transformers. We then establish a fundamental negative result, proving that any mechanism for sequential visual token generation under attention-based architectures must use at least $\Omega(n^2 d)$ memory, when $d = \Omega(\log n)$, where $n$ is the number of tokens generated and $d$ is the embedding dimensionality. This result demonstrates that achieving truly sub-quadratic memory usage is impossible without additional structural constraints. Our proof is constructed via a reduction from a computational lower bound problem, leveraging randomized embedding techniques inspired by dimensionality reduction principles. Finally, we discuss how sparsity priors on visual representations can influence memory efficiency, presenting both impossibility results and potential directions for mitigating memory overhead.

Limits of KV Cache Compression for Tensor Attention based Autoregressive Transformers

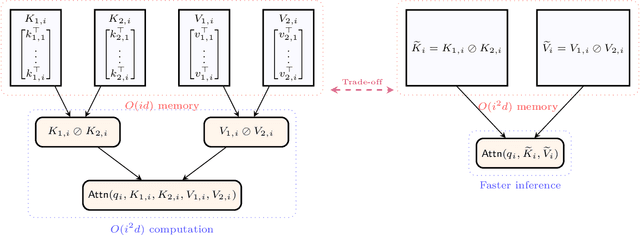
The key-value (KV) cache in autoregressive transformers presents a significant bottleneck during inference, which restricts the context length capabilities of large language models (LLMs). While previous work analyzes the fundamental space complexity barriers in standard attention mechanism [Haris and Onak, 2025], our work generalizes the space complexity barriers result to tensor attention version. Our theoretical contributions rely on a novel reduction from communication complexity and deduce the memory lower bound for tensor-structured attention mechanisms when $d = \Omega(\log n)$. In the low dimensional regime where $d = o(\log n)$, we analyze the theoretical bounds of the space complexity as well. Overall, our work provides a theoretical foundation for us to understand the compression-expressivity tradeoff in tensor attention mechanisms and offers more perspectives in developing more memory-efficient transformer architectures.

Learning to Inference Adaptively for Multimodal Large Language Models

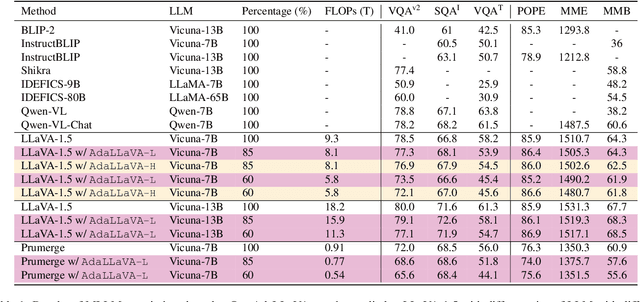
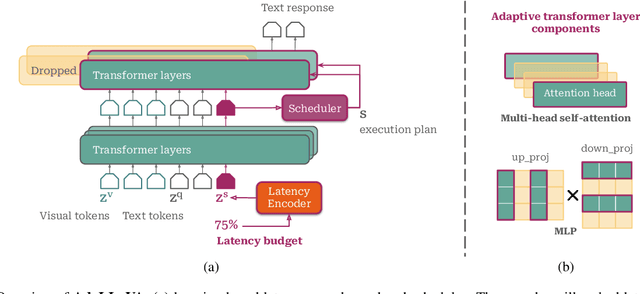
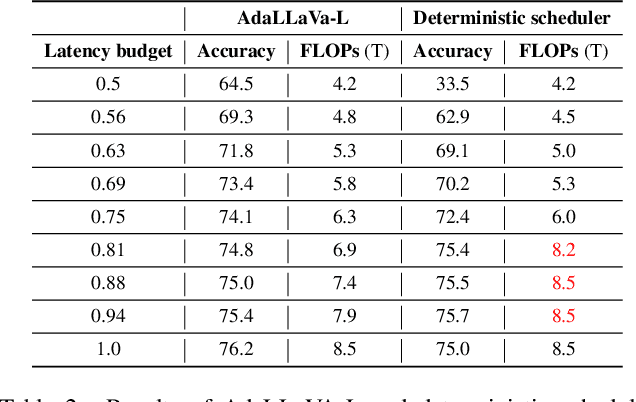
Multimodal Large Language Models (MLLMs) have shown impressive capabilities in reasoning, yet come with substantial computational cost, limiting their deployment in resource-constrained settings. Despite recent efforts on improving the efficiency of MLLMs, prior solutions fall short in responding to varying runtime conditions, in particular changing resource availability (e.g., contention due to the execution of other programs on the device). To bridge this gap, we introduce AdaLLaVA, an adaptive inference framework that learns to dynamically reconfigure operations in an MLLM during inference, accounting for the input data and a latency budget. We conduct extensive experiments across benchmarks involving question-answering, reasoning, and hallucination. Our results show that AdaLLaVA effectively adheres to input latency budget, achieving varying accuracy and latency tradeoffs at runtime. Further, we demonstrate that AdaLLaVA adapts to both input latency and content, can be integrated with token selection for enhanced efficiency, and generalizes across MLLMs.Our project webpage with code release is at https://zhuoyan-xu.github.io/ada-llava/.

Theoretical Guarantees for High Order Trajectory Refinement in Generative Flows

Flow matching has emerged as a powerful framework for generative modeling, offering computational advantages over diffusion models by leveraging deterministic Ordinary Differential Equations (ODEs) instead of stochastic dynamics. While prior work established the worst case optimality of standard flow matching under Wasserstein distances, the theoretical guarantees for higher-order flow matching - which incorporates acceleration terms to refine sample trajectories - remain unexplored. In this paper, we bridge this gap by proving that higher-order flow matching preserves worst case optimality as a distribution estimator. We derive upper bounds on the estimation error for second-order flow matching, demonstrating that the convergence rates depend polynomially on the smoothness of the target distribution (quantified via Besov spaces) and key parameters of the ODE dynamics. Our analysis employs neural network approximations with carefully controlled depth, width, and sparsity to bound acceleration errors across both small and large time intervals, ultimately unifying these results into a general worst case optimal bound for all time steps.

HOFAR: High-Order Augmentation of Flow Autoregressive Transformers

Flow Matching and Transformer architectures have demonstrated remarkable performance in image generation tasks, with recent work FlowAR [Ren et al., 2024] synergistically integrating both paradigms to advance synthesis fidelity. However, current FlowAR implementations remain constrained by first-order trajectory modeling during the generation process. This paper introduces a novel framework that systematically enhances flow autoregressive transformers through high-order supervision. We provide theoretical analysis and empirical evaluation showing that our High-Order FlowAR (HOFAR) demonstrates measurable improvements in generation quality compared to baseline models. The proposed approach advances the understanding of flow-based autoregressive modeling by introducing a systematic framework for analyzing trajectory dynamics through high-order expansion.

Text-to-Image Diffusion Models Cannot Count, and Prompt Refinement Cannot Help

Generative modeling is widely regarded as one of the most essential problems in today's AI community, with text-to-image generation having gained unprecedented real-world impacts. Among various approaches, diffusion models have achieved remarkable success and have become the de facto solution for text-to-image generation. However, despite their impressive performance, these models exhibit fundamental limitations in adhering to numerical constraints in user instructions, frequently generating images with an incorrect number of objects. While several prior works have mentioned this issue, a comprehensive and rigorous evaluation of this limitation remains lacking. To address this gap, we introduce T2ICountBench, a novel benchmark designed to rigorously evaluate the counting ability of state-of-the-art text-to-image diffusion models. Our benchmark encompasses a diverse set of generative models, including both open-source and private systems. It explicitly isolates counting performance from other capabilities, provides structured difficulty levels, and incorporates human evaluations to ensure high reliability. Extensive evaluations with T2ICountBench reveal that all state-of-the-art diffusion models fail to generate the correct number of objects, with accuracy dropping significantly as the number of objects increases. Additionally, an exploratory study on prompt refinement demonstrates that such simple interventions generally do not improve counting accuracy. Our findings highlight the inherent challenges in numerical understanding within diffusion models and point to promising directions for future improvements.

Scaling Law Phenomena Across Regression Paradigms: Multiple and Kernel Approaches

Recently, Large Language Models (LLMs) have achieved remarkable success. A key factor behind this success is the scaling law observed by OpenAI. Specifically, for models with Transformer architecture, the test loss exhibits a power-law relationship with model size, dataset size, and the amount of computation used in training, demonstrating trends that span more than seven orders of magnitude. This scaling law challenges traditional machine learning wisdom, notably the Oscar Scissors principle, which suggests that an overparametrized algorithm will overfit the training datasets, resulting in poor test performance. Recent research has also identified the scaling law in simpler machine learning contexts, such as linear regression. However, fully explaining the scaling law in large practical models remains an elusive goal. In this work, we advance our understanding by demonstrating that the scaling law phenomenon extends to multiple regression and kernel regression settings, which are significantly more expressive and powerful than linear methods. Our analysis provides deeper insights into the scaling law, potentially enhancing our understanding of LLMs.

When Can We Solve the Weighted Low Rank Approximation Problem in Truly Subquadratic Time?

The weighted low-rank approximation problem is a fundamental numerical linear algebra problem and has many applications in machine learning. Given a $n \times n$ weight matrix $W$ and a $n \times n$ matrix $A$, the goal is to find two low-rank matrices $U, V \in \mathbb{R}^{n \times k}$ such that the cost of $\| W \circ (U V^\top - A) \|_F^2$ is minimized. Previous work has to pay $\Omega(n^2)$ time when matrices $A$ and $W$ are dense, e.g., having $\Omega(n^2)$ non-zero entries. In this work, we show that there is a certain regime, even if $A$ and $W$ are dense, we can still hope to solve the weighted low-rank approximation problem in almost linear $n^{1+o(1)}$ time.

On Computational Limits of FlowAR Models: Expressivity and Efficiency

The expressive power and computational complexity of deep visual generative models, such as flow-based and autoregressive (AR) models, have gained considerable interest for their wide-ranging applications in generative tasks. However, the theoretical characterization of their expressiveness through the lens of circuit complexity remains underexplored, particularly for the state-of-the-art architecture like FlowAR proposed by [Ren et al., 2024], which integrates flow-based and autoregressive mechanisms. This gap limits our understanding of their inherent computational limits and practical efficiency. In this study, we address this gap by analyzing the circuit complexity of the FlowAR architecture. We demonstrate that when the largest feature map produced by the FlowAR model has dimensions $n \times n \times c$, the FlowAR model is simulable by a family of threshold circuits $\mathsf{TC}^0$, which have constant depth $O(1)$ and polynomial width $\mathrm{poly}(n)$. This is the first study to rigorously highlight the limitations in the expressive power of FlowAR models. Furthermore, we identify the conditions under which the FlowAR model computations can achieve almost quadratic time. To validate our theoretical findings, we present efficient model variant constructions based on low-rank approximations that align with the derived criteria. Our work provides a foundation for future comparisons with other generative paradigms and guides the development of more efficient and expressive implementations.