Text-to-Image Diffusion Models Cannot Count, and Prompt Refinement Cannot Help

Generative modeling is widely regarded as one of the most essential problems in today's AI community, with text-to-image generation having gained unprecedented real-world impacts. Among various approaches, diffusion models have achieved remarkable success and have become the de facto solution for text-to-image generation. However, despite their impressive performance, these models exhibit fundamental limitations in adhering to numerical constraints in user instructions, frequently generating images with an incorrect number of objects. While several prior works have mentioned this issue, a comprehensive and rigorous evaluation of this limitation remains lacking. To address this gap, we introduce T2ICountBench, a novel benchmark designed to rigorously evaluate the counting ability of state-of-the-art text-to-image diffusion models. Our benchmark encompasses a diverse set of generative models, including both open-source and private systems. It explicitly isolates counting performance from other capabilities, provides structured difficulty levels, and incorporates human evaluations to ensure high reliability. Extensive evaluations with T2ICountBench reveal that all state-of-the-art diffusion models fail to generate the correct number of objects, with accuracy dropping significantly as the number of objects increases. Additionally, an exploratory study on prompt refinement demonstrates that such simple interventions generally do not improve counting accuracy. Our findings highlight the inherent challenges in numerical understanding within diffusion models and point to promising directions for future improvements.

Simulation of Hypergraph Algorithms with Looped Transformers

Looped Transformers have shown exceptional capability in simulating traditional graph algorithms, but their application to more complex structures like hypergraphs remains underexplored. Hypergraphs generalize graphs by modeling higher-order relationships among multiple entities, enabling richer representations but introducing significant computational challenges. In this work, we extend the Loop Transformer architecture to simulate hypergraph algorithms efficiently, addressing the gap between neural networks and combinatorial optimization over hypergraphs. In this paper, we extend the Loop Transformer architecture to simulate hypergraph algorithms efficiently, addressing the gap between neural networks and combinatorial optimization over hypergraphs. Specifically, we propose a novel degradation mechanism for reducing hypergraphs to graph representations, enabling the simulation of graph-based algorithms, such as Dijkstra's shortest path. Furthermore, we introduce a hyperedge-aware encoding scheme to simulate hypergraph-specific algorithms, exemplified by Helly's algorithm. The paper establishes theoretical guarantees for these simulations, demonstrating the feasibility of processing high-dimensional and combinatorial data using Loop Transformers. This work highlights the potential of Transformers as general-purpose algorithmic solvers for structured data.

A novel particle swarm optimizer with multi-stage transformation and genetic operation for VLSI routing

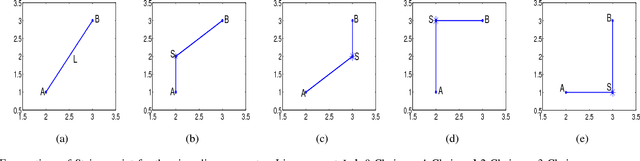
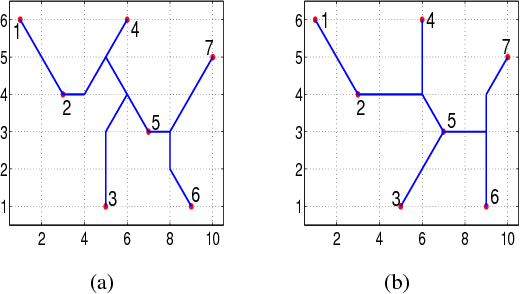
As the basic model for very large scale integration (VLSI) routing, the Steiner minimal tree (SMT) can be used in various practical problems, such as wire length optimization, congestion, and time delay estimation. In this paper, a novel particle swarm optimization (PSO) algorithm based on multi-stage transformation and genetic operation is presented to construct two types of SMT, including non-Manhattan SMT and Manhattan SMT. Firstly, in order to be able to handle two types of SMT problems at the same time, an effective edge-vertex encoding strategy is proposed. Secondly, a multi-stage transformation strategy is proposed to both expand the algorithm search space and ensure the effective convergence. We have tested three types from two to four stages and various combinations under each type to highlight the best combination. Thirdly, the genetic operators combined with union-find partition are designed to construct the discrete particle update formula for discrete VLSI routing. Moreover, in order to introduce uncertainty and diversity into the search of PSO algorithm, we propose an improved mutation operation with edge transformation. Experimental results show that our algorithm from a global perspective of multilayer structure can achieve the best solution quality among the existing algorithms. Finally, to our best knowledge, it is the first work to address both manhattan and non-manhattan routing at the same time.