Unlocking the Theory Behind Scaling 1-Bit Neural Networks
Paper and Code
Nov 03, 2024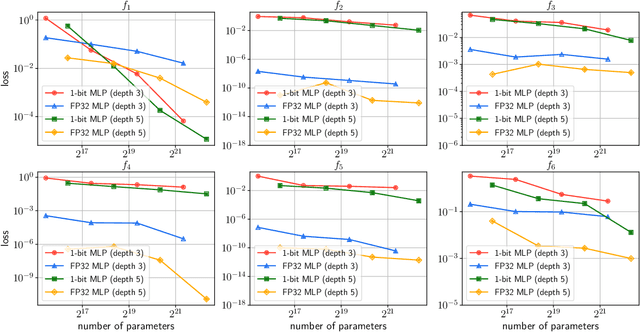
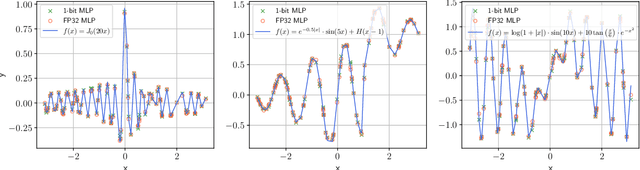
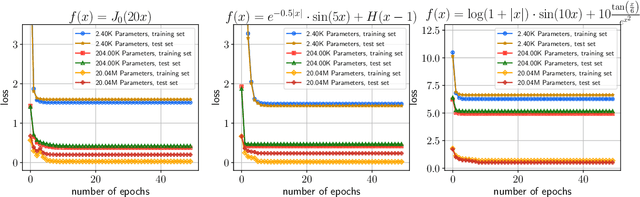
Recently, 1-bit Large Language Models (LLMs) have emerged, showcasing an impressive combination of efficiency and performance that rivals traditional LLMs. Research by Wang et al. (2023); Ma et al. (2024) indicates that the performance of these 1-bit LLMs progressively improves as the number of parameters increases, hinting at the potential existence of a Scaling Law for 1-bit Neural Networks. In this paper, we present the first theoretical result that rigorously establishes this scaling law for 1-bit models. We prove that, despite the constraint of weights restricted to $\{-1, +1\}$, the dynamics of model training inevitably align with kernel behavior as the network width grows. This theoretical breakthrough guarantees convergence of the 1-bit model to an arbitrarily small loss as width increases. Furthermore, we introduce the concept of the generalization difference, defined as the gap between the outputs of 1-bit networks and their full-precision counterparts, and demonstrate that this difference maintains a negligible level as network width scales. Building on the work of Kaplan et al. (2020), we conclude by examining how the training loss scales as a power-law function of the model size, dataset size, and computational resources utilized for training. Our findings underscore the promising potential of scaling 1-bit neural networks, suggesting that int1 could become the standard in future neural network precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge