Leverage Score Sampling for Tensor Product Matrices in Input Sparsity Time
Paper and Code
Feb 09, 2022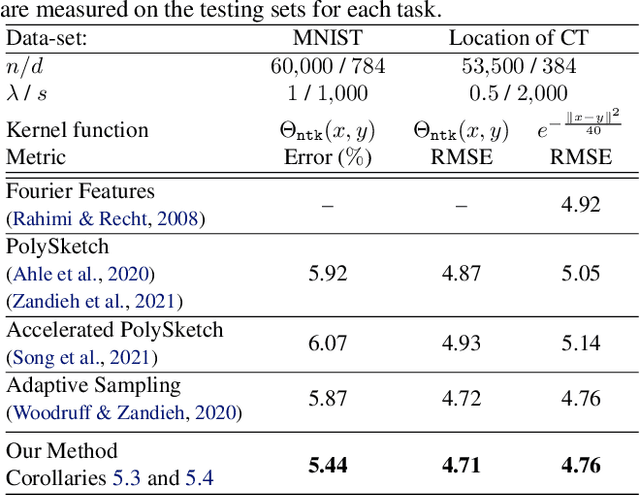
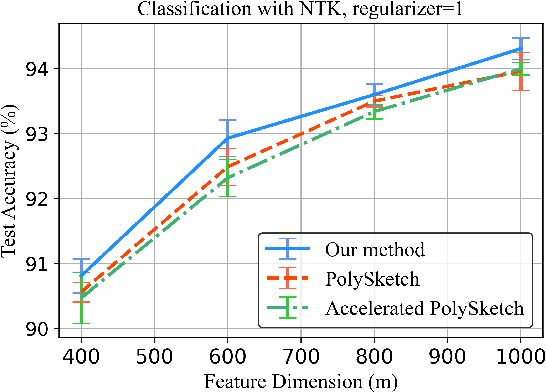
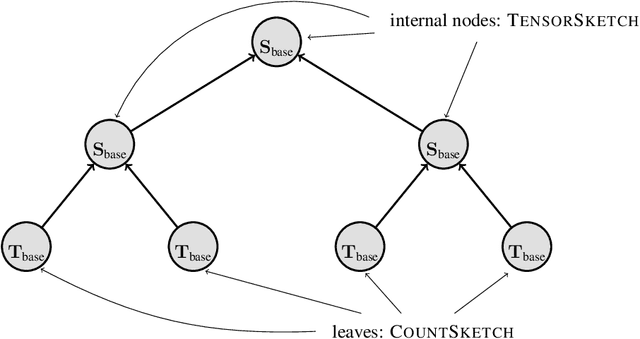
We give an input sparsity time sampling algorithm for spectrally approximating the Gram matrix corresponding to the $q$-fold column-wise tensor product of $q$ matrices using a nearly optimal number of samples, improving upon all previously known methods by poly$(q)$ factors. Furthermore, for the important special care of the $q$-fold self-tensoring of a dataset, which is the feature matrix of the degree-$q$ polynomial kernel, the leading term of our method's runtime is proportional to the size of the dataset and has no dependence on $q$. Previous techniques either incur a poly$(q)$ factor slowdown in their runtime or remove the dependence on $q$ at the expense of having sub-optimal target dimension, and depend quadratically on the number of data-points in their runtime. Our sampling technique relies on a collection of $q$ partially correlated random projections which can be simultaneously applied to a dataset $X$ in total time that only depends on the size of $X$, and at the same time their $q$-fold Kronecker product acts as a near-isometry for any fixed vector in the column span of $X^{\otimes q}$. We show that our sampling methods generalize to other classes of kernels beyond polynomial, such as Gaussian and Neural Tangent kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge