TinyGSM: achieving >80% on GSM8k with small language models

Small-scale models offer various computational advantages, and yet to which extent size is critical for problem-solving abilities remains an open question. Specifically for solving grade school math, the smallest model size so far required to break the 80\% barrier on the GSM8K benchmark remains to be 34B. Our work studies how high-quality datasets may be the key for small language models to acquire mathematical reasoning. We introduce \texttt{TinyGSM}, a synthetic dataset of 12.3M grade school math problems paired with Python solutions, generated fully by GPT-3.5. After finetuning on \texttt{TinyGSM}, we find that a duo of a 1.3B generation model and a 1.3B verifier model can achieve 81.5\% accuracy, outperforming existing models that are orders of magnitude larger. This also rivals the performance of the GPT-3.5 ``teacher'' model (77.4\%), from which our model's training data is generated. Our approach is simple and has two key components: 1) the high-quality dataset \texttt{TinyGSM}, 2) the use of a verifier, which selects the final outputs from multiple candidate generations.

AutoMoE: Neural Architecture Search for Efficient Sparsely Activated Transformers

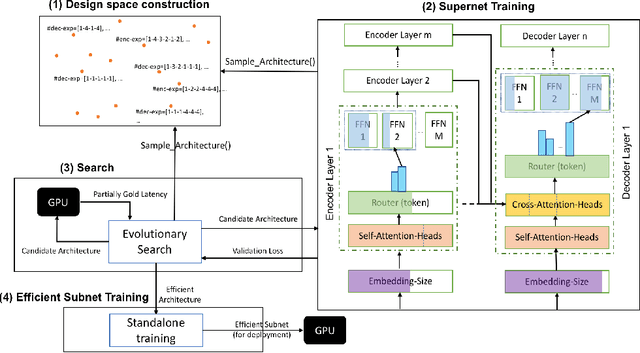
Neural architecture search (NAS) has demonstrated promising results on identifying efficient Transformer architectures which outperform manually designed ones for natural language tasks like neural machine translation (NMT). Existing NAS methods operate on a space of dense architectures, where all of the sub-architecture weights are activated for every input. Motivated by the recent advances in sparsely activated models like the Mixture-of-Experts (MoE) model, we introduce sparse architectures with conditional computation into the NAS search space. Given this expressive search space which subsumes prior densely activated architectures, we develop a new framework AutoMoE to search for efficient sparsely activated sub-Transformers. AutoMoE-generated sparse models obtain (i) 3x FLOPs reduction over manually designed dense Transformers and (ii) 23% FLOPs reduction over state-of-the-art NAS-generated dense sub-Transformers with parity in BLEU score on benchmark datasets for NMT. AutoMoE consists of three training phases: (a) Heterogeneous search space design with dense and sparsely activated Transformer modules (e.g., how many experts? where to place them? what should be their sizes?); (b) SuperNet training that jointly trains several subnetworks sampled from the large search space by weight-sharing; (c) Evolutionary search for the architecture with the optimal trade-off between task performance and computational constraint like FLOPs and latency. AutoMoE code, data and trained models are available at https://github.com/microsoft/AutoMoE.

LiteTransformerSearch: Training-free On-device Search for Efficient Autoregressive Language Models

The transformer architecture is ubiquitously used as the building block of most large-scale language models. However, it remains a painstaking guessing game of trial and error to set its myriad of architectural hyperparameters, e.g., number of layers, number of attention heads, and inner size of the feed forward network, and find architectures with the optimal trade-off between task performance like perplexity and compute constraints like memory and latency. This challenge is further exacerbated by the proliferation of various hardware. In this work, we leverage the somewhat surprising empirical observation that the number of non-embedding parameters in autoregressive transformers has a high rank correlation with task performance, irrespective of the architectural hyperparameters. Since architectural hyperparameters affect the latency and memory footprint in a hardware-dependent manner, the above observation organically induces a simple search algorithm that can be directly run on target devices. We rigorously show that the latency and perplexity pareto-frontier can be found without need for any model training, using non-embedding parameters as a proxy for perplexity. We evaluate our method, dubbed Lightweight Transformer Search (LTS), on diverse devices from ARM CPUs to Nvidia GPUs and show that the perplexity of Transformer-XL can be achieved with up to 2x lower latency. LTS extracts the pareto-frontier in less than 3 hours while running on a commodity laptop. We effectively remove the carbon footprint of training for hundreds of GPU hours, offering a strong simple baseline for future NAS methods in autoregressive language modeling.

FEAR: A Simple Lightweight Method to Rank Architectures

The fundamental problem in Neural Architecture Search (NAS) is to efficiently find high-performing architectures from a given search space. We propose a simple but powerful method which we call FEAR, for ranking architectures in any search space. FEAR leverages the viewpoint that neural networks are powerful non-linear feature extractors. First, we train different architectures in the search space to the same training or validation error. Then, we compare the usefulness of the features extracted by each architecture. We do so with a quick training keeping most of the architecture frozen. This gives fast estimates of the relative performance. We validate FEAR on Natsbench topology search space on three different datasets against competing baselines and show strong ranking correlation especially compared to recently proposed zero-cost methods. FEAR particularly excels at ranking high-performance architectures in the search space. When used in the inner loop of discrete search algorithms like random search, FEAR can cut down the search time by approximately 2.4X without losing accuracy. We additionally empirically study very recently proposed zero-cost measures for ranking and find that they breakdown in ranking performance as training proceeds and also that data-agnostic ranking scores which ignore the dataset do not generalize across dissimilar datasets.

Provably Robust Deep Learning via Adversarially Trained Smoothed Classifiers

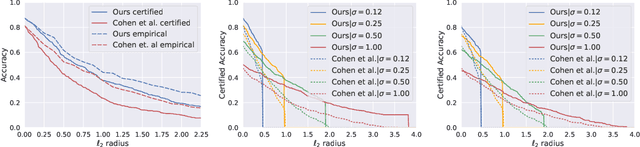
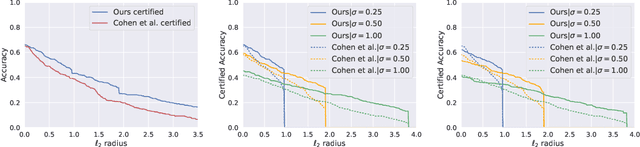
Recent works have shown the effectiveness of randomized smoothing as a scalable technique for building neural network-based classifiers that are provably robust to $\ell_2$-norm adversarial perturbations. In this paper, we employ adversarial training to improve the performance of randomized smoothing. We design an adapted attack for smoothed classifiers, and we show how this attack can be used in an adversarial training setting to boost the provable robustness of smoothed classifiers. We demonstrate through extensive experimentation that our method consistently outperforms all existing provably $\ell_2$-robust classifiers by a significant margin on ImageNet and CIFAR-10, establishing the state-of-the-art for provable $\ell_2$-defenses. Our code and trained models are available at http://github.com/Hadisalman/smoothing-adversarial .

Is Q-learning Provably Efficient?

Model-free reinforcement learning (RL) algorithms, such as Q-learning, directly parameterize and update value functions or policies without explicitly modeling the environment. They are typically simpler, more flexible to use, and thus more prevalent in modern deep RL than model-based approaches. However, empirical work has suggested that model-free algorithms may require more samples to learn [Deisenroth and Rasmussen 2011, Schulman et al. 2015]. The theoretical question of "whether model-free algorithms can be made sample efficient" is one of the most fundamental questions in RL, and remains unsolved even in the basic scenario with finitely many states and actions. We prove that, in an episodic MDP setting, Q-learning with UCB exploration achieves regret $\tilde{O}(\sqrt{H^3 SAT})$, where $S$ and $A$ are the numbers of states and actions, $H$ is the number of steps per episode, and $T$ is the total number of steps. This sample efficiency matches the optimal regret that can be achieved by any model-based approach, up to a single $\sqrt{H}$ factor. To the best of our knowledge, this is the first analysis in the model-free setting that establishes $\sqrt{T}$ regret without requiring access to a "simulator."

On Finding the Largest Mean Among Many

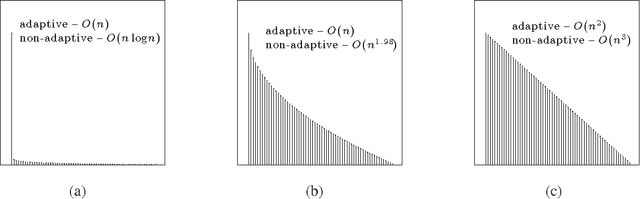
Sampling from distributions to find the one with the largest mean arises in a broad range of applications, and it can be mathematically modeled as a multi-armed bandit problem in which each distribution is associated with an arm. This paper studies the sample complexity of identifying the best arm (largest mean) in a multi-armed bandit problem. Motivated by large-scale applications, we are especially interested in identifying situations where the total number of samples that are necessary and sufficient to find the best arm scale linearly with the number of arms. We present a single-parameter multi-armed bandit model that spans the range from linear to superlinear sample complexity. We also give a new algorithm for best arm identification, called PRISM, with linear sample complexity for a wide range of mean distributions. The algorithm, like most exploration procedures for multi-armed bandits, is adaptive in the sense that the next arms to sample are selected based on previous samples. We compare the sample complexity of adaptive procedures with simpler non-adaptive procedures using new lower bounds. For many problem instances, the increased sample complexity required by non-adaptive procedures is a polynomial factor of the number of arms.

Optimal discovery with probabilistic expert advice: finite time analysis and macroscopic optimality

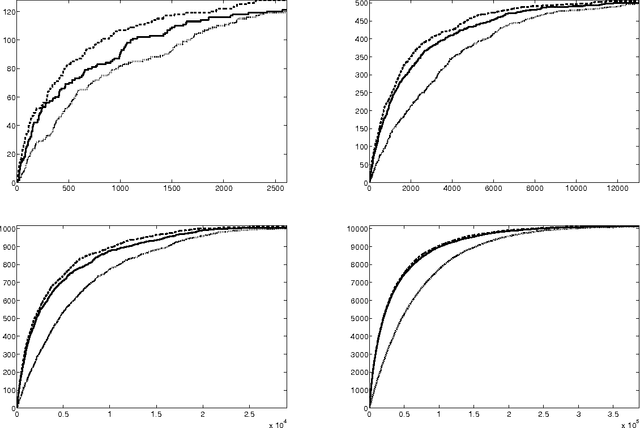
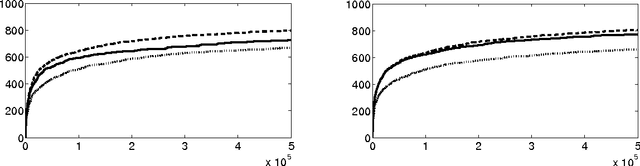
We consider an original problem that arises from the issue of security analysis of a power system and that we name optimal discovery with probabilistic expert advice. We address it with an algorithm based on the optimistic paradigm and on the Good-Turing missing mass estimator. We prove two different regret bounds on the performance of this algorithm under weak assumptions on the probabilistic experts. Under more restrictive hypotheses, we also prove a macroscopic optimality result, comparing the algorithm both with an oracle strategy and with uniform sampling. Finally, we provide numerical experiments illustrating these theoretical findings.

The best of both worlds: stochastic and adversarial bandits

We present a new bandit algorithm, SAO (Stochastic and Adversarial Optimal), whose regret is, essentially, optimal both for adversarial rewards and for stochastic rewards. Specifically, SAO combines the square-root worst-case regret of Exp3 (Auer et al., SIAM J. on Computing 2002) and the (poly)logarithmic regret of UCB1 (Auer et al., Machine Learning 2002) for stochastic rewards. Adversarial rewards and stochastic rewards are the two main settings in the literature on (non-Bayesian) multi-armed bandits. Prior work on multi-armed bandits treats them separately, and does not attempt to jointly optimize for both. Our result falls into a general theme of achieving good worst-case performance while also taking advantage of "nice" problem instances, an important issue in the design of algorithms with partially known inputs.

Minimax Policies for Combinatorial Prediction Games

We address the online linear optimization problem when the actions of the forecaster are represented by binary vectors. Our goal is to understand the magnitude of the minimax regret for the worst possible set of actions. We study the problem under three different assumptions for the feedback: full information, and the partial information models of the so-called "semi-bandit", and "bandit" problems. We consider both $L_\infty$-, and $L_2$-type of restrictions for the losses assigned by the adversary. We formulate a general strategy using Bregman projections on top of a potential-based gradient descent, which generalizes the ones studied in the series of papers Gyorgy et al. (2007), Dani et al. (2008), Abernethy et al. (2008), Cesa-Bianchi and Lugosi (2009), Helmbold and Warmuth (2009), Koolen et al. (2010), Uchiya et al. (2010), Kale et al. (2010) and Audibert and Bubeck (2010). We provide simple proofs that recover most of the previous results. We propose new upper bounds for the semi-bandit game. Moreover we derive lower bounds for all three feedback assumptions. With the only exception of the bandit game, the upper and lower bounds are tight, up to a constant factor. Finally, we answer a question asked by Koolen et al. (2010) by showing that the exponentially weighted average forecaster is suboptimal against $L_{\infty}$ adversaries.