Convergence of continuous-time stochastic gradient descent with applications to linear deep neural networks

We study a continuous-time approximation of the stochastic gradient descent process for minimizing the expected loss in learning problems. The main results establish general sufficient conditions for the convergence, extending the results of Chatterjee (2022) established for (nonstochastic) gradient descent. We show how the main result can be applied to the case of overparametrized linear neural network training.

A note on estimating the dimension from a random geometric graph

Let $G_n$ be a random geometric graph with vertex set $[n]$ based on $n$ i.i.d.\ random vectors $X_1,\ldots,X_n$ drawn from an unknown density $f$ on $\R^d$. An edge $(i,j)$ is present when $\|X_i -X_j\| \le r_n$, for a given threshold $r_n$ possibly depending upon $n$, where $\| \cdot \|$ denotes Euclidean distance. We study the problem of estimating the dimension $d$ of the underlying space when we have access to the adjacency matrix of the graph but do not know $r_n$ or the vectors $X_i$. The main result of the paper is that there exists an estimator of $d$ that converges to $d$ in probability as $n \to \infty$ for all densities with $\int f^5 < \infty$ whenever $n^{3/2} r_n^d \to \infty$ and $r_n = o(1)$. The conditions allow very sparse graphs since when $n^{3/2} r_n^d \to 0$, the graph contains isolated edges only, with high probability. We also show that, without any condition on the density, a consistent estimator of $d$ exists when $n r_n^d \to \infty$ and $r_n = o(1)$.

Broadcasting in random recursive dags

A uniform $k$-{\sc dag} generalizes the uniform random recursive tree by picking $k$ parents uniformly at random from the existing nodes. It starts with $k$ ''roots''. Each of the $k$ roots is assigned a bit. These bits are propagated by a noisy channel. The parents' bits are flipped with probability $p$, and a majority vote is taken. When all nodes have received their bits, the $k$-{\sc dag} is shown without identifying the roots. The goal is to estimate the majority bit among the roots. We identify the threshold for $p$ as a function of $k$ below which the majority rule among all nodes yields an error $c+o(1)$ with $c<1/2$. Above the threshold the majority rule errs with probability $1/2+o(1)$.

Multivariate mean estimation with direction-dependent accuracy

We consider the problem of estimating the mean of a random vector based on $N$ independent, identically distributed observations. We prove the existence of an estimator that has a near-optimal error in all directions in which the variance of the one dimensional marginal of the random vector is not too small: with probability $1-\delta$, the procedure returns $\wh{\mu}_N$ which satisfies that for every direction $u \in S^{d-1}$, \[ \inr{\wh{\mu}_N - \mu, u}\le \frac{C}{\sqrt{N}} \left( \sigma(u)\sqrt{\log(1/\delta)} + \left(\E\|X-\EXP X\|_2^2\right)^{1/2} \right)~, \] where $\sigma^2(u) = \var(\inr{X,u})$ and $C$ is a constant. To achieve this, we require only slightly more than the existence of the covariance matrix, in the form of a certain moment-equivalence assumption. The proof relies on novel bounds for the ratio of empirical and true probabilities that hold uniformly over certain classes of random variables.

On Mean Estimation for Heteroscedastic Random Variables

We study the problem of estimating the common mean $\mu$ of $n$ independent symmetric random variables with different and unknown standard deviations $\sigma_1 \le \sigma_2 \le \cdots \le\sigma_n$. We show that, under some mild regularity assumptions on the distribution, there is a fully adaptive estimator $\widehat{\mu}$ such that it is invariant to permutations of the elements of the sample and satisfies that, up to logarithmic factors, with high probability, \[ |\widehat{\mu} - \mu| \lesssim \min\left\{\sigma_{m^*}, \frac{\sqrt{n}}{\sum_{i = \sqrt{n}}^n \sigma_i^{-1}} \right\}~, \] where the index $m^* \lesssim \sqrt{n}$ satisfies $m^* \approx \sqrt{\sigma_{m^*}\sum_{i = m^*}^n\sigma_i^{-1}}$.

Mean estimation and regression under heavy-tailed distributions--a survey

We survey some of the recent advances in mean estimation and regression function estimation. In particular, we describe sub-Gaussian mean estimators for possibly heavy-tailed data both in the univariate and multivariate settings. We focus on estimators based on median-of-means techniques but other methods such as the trimmed mean and Catoni's estimator are also reviewed. We give detailed proofs for the cornerstone results. We dedicate a section on statistical learning problems--in particular, regression function estimation--in the presence of possibly heavy-tailed data.

Multiplayer bandits without observing collision information

We study multiplayer stochastic multi-armed bandit problems in which the players cannot communicate, and if two or more players pull the same arm, a collision occurs and the involved players receive zero reward. We consider two feedback models: a model in which the players can observe whether a collision has occurred, and a more difficult setup when no collision information is available. We give the first theoretical guarantees for the second model: an algorithm with a logarithmic regret, and an algorithm with a square-root regret type that does not depend on the gaps between the means. For the first model, we give the first square-root regret bounds that do not depend on the gaps. Building on these ideas, we also give an algorithm for reaching approximate Nash equilibria quickly in stochastic anti-coordination games.

Mirror Descent Meets Fixed Share (and feels no regret)

Mirror descent with an entropic regularizer is known to achieve shifting regret bounds that are logarithmic in the dimension. This is done using either a carefully designed projection or by a weight sharing technique. Via a novel unified analysis, we show that these two approaches deliver essentially equivalent bounds on a notion of regret generalizing shifting, adaptive, discounted, and other related regrets. Our analysis also captures and extends the generalized weight sharing technique of Bousquet and Warmuth, and can be refined in several ways, including improvements for small losses and adaptive tuning of parameters.

Minimax Policies for Combinatorial Prediction Games

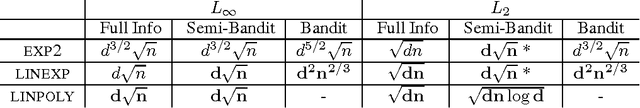
We address the online linear optimization problem when the actions of the forecaster are represented by binary vectors. Our goal is to understand the magnitude of the minimax regret for the worst possible set of actions. We study the problem under three different assumptions for the feedback: full information, and the partial information models of the so-called "semi-bandit", and "bandit" problems. We consider both $L_\infty$-, and $L_2$-type of restrictions for the losses assigned by the adversary. We formulate a general strategy using Bregman projections on top of a potential-based gradient descent, which generalizes the ones studied in the series of papers Gyorgy et al. (2007), Dani et al. (2008), Abernethy et al. (2008), Cesa-Bianchi and Lugosi (2009), Helmbold and Warmuth (2009), Koolen et al. (2010), Uchiya et al. (2010), Kale et al. (2010) and Audibert and Bubeck (2010). We provide simple proofs that recover most of the previous results. We propose new upper bounds for the semi-bandit game. Moreover we derive lower bounds for all three feedback assumptions. With the only exception of the bandit game, the upper and lower bounds are tight, up to a constant factor. Finally, we answer a question asked by Koolen et al. (2010) by showing that the exponentially weighted average forecaster is suboptimal against $L_{\infty}$ adversaries.

Online Multi-task Learning with Hard Constraints

We discuss multi-task online learning when a decision maker has to deal simultaneously with M tasks. The tasks are related, which is modeled by imposing that the M-tuple of actions taken by the decision maker needs to satisfy certain constraints. We give natural examples of such restrictions and then discuss a general class of tractable constraints, for which we introduce computationally efficient ways of selecting actions, essentially by reducing to an on-line shortest path problem. We briefly discuss "tracking" and "bandit" versions of the problem and extend the model in various ways, including non-additive global losses and uncountably infinite sets of tasks.