Regret in Online Combinatorial Optimization

We address online linear optimization problems when the possible actions of the decision maker are represented by binary vectors. The regret of the decision maker is the difference between her realized loss and the best loss she would have achieved by picking, in hindsight, the best possible action. Our goal is to understand the magnitude of the best possible (minimax) regret. We study the problem under three different assumptions for the feedback the decision maker receives: full information, and the partial information models of the so-called "semi-bandit" and "bandit" problems. Combining the Mirror Descent algorithm and the INF (Implicitely Normalized Forecaster) strategy, we are able to prove optimal bounds for the semi-bandit case. We also recover the optimal bounds for the full information setting. In the bandit case we discuss existing results in light of a new lower bound, and suggest a conjecture on the optimal regret in that case. Finally we also prove that the standard exponentially weighted average forecaster is provably suboptimal in the setting of online combinatorial optimization.

Regret lower bounds and extended Upper Confidence Bounds policies in stochastic multi-armed bandit problem

This paper is devoted to regret lower bounds in the classical model of stochastic multi-armed bandit. A well-known result of Lai and Robbins, which has then been extended by Burnetas and Katehakis, has established the presence of a logarithmic bound for all consistent policies. We relax the notion of consistence, and exhibit a generalisation of the logarithmic bound. We also show the non existence of logarithmic bound in the general case of Hannan consistency. To get these results, we study variants of popular Upper Confidence Bounds (ucb) policies. As a by-product, we prove that it is impossible to design an adaptive policy that would select the best of two algorithms by taking advantage of the properties of the environment.

Robustness of Anytime Bandit Policies

This paper studies the deviations of the regret in a stochastic multi-armed bandit problem. When the total number of plays n is known beforehand by the agent, Audibert et al. (2009) exhibit a policy such that with probability at least 1-1/n, the regret of the policy is of order log(n). They have also shown that such a property is not shared by the popular ucb1 policy of Auer et al. (2002). This work first answers an open question: it extends this negative result to any anytime policy. The second contribution of this paper is to design anytime robust policies for specific multi-armed bandit problems in which some restrictions are put on the set of possible distributions of the different arms.

Minimax Policies for Combinatorial Prediction Games

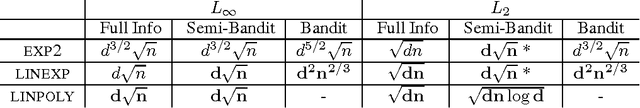
We address the online linear optimization problem when the actions of the forecaster are represented by binary vectors. Our goal is to understand the magnitude of the minimax regret for the worst possible set of actions. We study the problem under three different assumptions for the feedback: full information, and the partial information models of the so-called "semi-bandit", and "bandit" problems. We consider both $L_\infty$-, and $L_2$-type of restrictions for the losses assigned by the adversary. We formulate a general strategy using Bregman projections on top of a potential-based gradient descent, which generalizes the ones studied in the series of papers Gyorgy et al. (2007), Dani et al. (2008), Abernethy et al. (2008), Cesa-Bianchi and Lugosi (2009), Helmbold and Warmuth (2009), Koolen et al. (2010), Uchiya et al. (2010), Kale et al. (2010) and Audibert and Bubeck (2010). We provide simple proofs that recover most of the previous results. We propose new upper bounds for the semi-bandit game. Moreover we derive lower bounds for all three feedback assumptions. With the only exception of the bandit game, the upper and lower bounds are tight, up to a constant factor. Finally, we answer a question asked by Koolen et al. (2010) by showing that the exponentially weighted average forecaster is suboptimal against $L_{\infty}$ adversaries.

Risk bounds in linear regression through PAC-Bayesian truncation

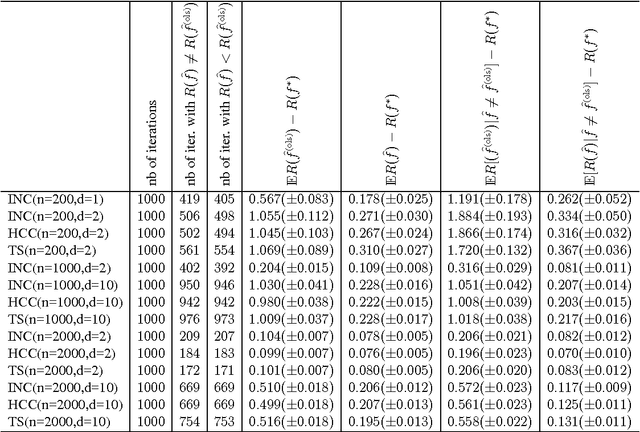
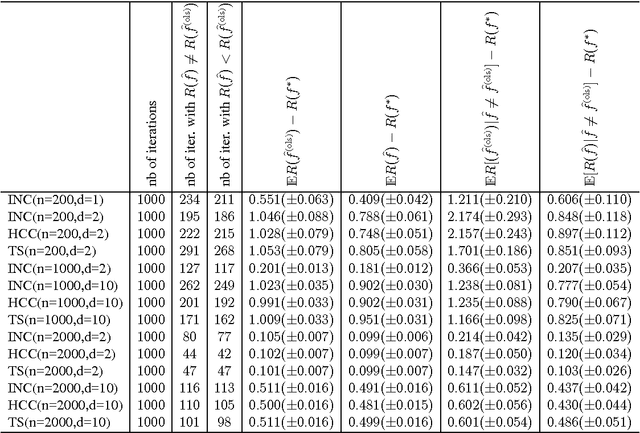
We consider the problem of predicting as well as the best linear combination of d given functions in least squares regression, and variants of this problem including constraints on the parameters of the linear combination. When the input distribution is known, there already exists an algorithm having an expected excess risk of order d/n, where n is the size of the training data. Without this strong assumption, standard results often contain a multiplicative log n factor, and require some additional assumptions like uniform boundedness of the d-dimensional input representation and exponential moments of the output. This work provides new risk bounds for the ridge estimator and the ordinary least squares estimator, and their variants. It also provides shrinkage procedures with convergence rate d/n (i.e., without the logarithmic factor) in expectation and in deviations, under various assumptions. The key common surprising factor of these results is the absence of exponential moment condition on the output distribution while achieving exponential deviations. All risk bounds are obtained through a PAC-Bayesian analysis on truncated differences of losses. Finally, we show that some of these results are not particular to the least squares loss, but can be generalized to similar strongly convex loss functions.

Structured Variable Selection with Sparsity-Inducing Norms

We consider the empirical risk minimization problem for linear supervised learning, with regularization by structured sparsity-inducing norms. These are defined as sums of Euclidean norms on certain subsets of variables, extending the usual $\ell_1$-norm and the group $\ell_1$-norm by allowing the subsets to overlap. This leads to a specific set of allowed nonzero patterns for the solutions of such problems. We first explore the relationship between the groups defining the norm and the resulting nonzero patterns, providing both forward and backward algorithms to go back and forth from groups to patterns. This allows the design of norms adapted to specific prior knowledge expressed in terms of nonzero patterns. We also present an efficient active set algorithm, and analyze the consistency of variable selection for least-squares linear regression in low and high-dimensional settings.

Graph Laplacians and their convergence on random neighborhood graphs

Given a sample from a probability measure with support on a submanifold in Euclidean space one can construct a neighborhood graph which can be seen as an approximation of the submanifold. The graph Laplacian of such a graph is used in several machine learning methods like semi-supervised learning, dimensionality reduction and clustering. In this paper we determine the pointwise limit of three different graph Laplacians used in the literature as the sample size increases and the neighborhood size approaches zero. We show that for a uniform measure on the submanifold all graph Laplacians have the same limit up to constants. However in the case of a non-uniform measure on the submanifold only the so called random walk graph Laplacian converges to the weighted Laplace-Beltrami operator.