Markov substitute processes : a new model for linguistics and beyond

We introduce Markov substitute processes, a new model at the crossroad of statistics and formal grammars, and prove its main property : Markov substitute processes with a given support form an exponential family.

Toric grammars: a new statistical approach to natural language modeling

We propose a new statistical model for computational linguistics. Rather than trying to estimate directly the probability distribution of a random sentence of the language, we define a Markov chain on finite sets of sentences with many finite recurrent communicating classes and define our language model as the invariant probability measures of the chain on each recurrent communicating class. This Markov chain, that we call a communication model, recombines at each step randomly the set of sentences forming its current state, using some grammar rules. When the grammar rules are fixed and known in advance instead of being estimated on the fly, we can prove supplementary mathematical properties. In particular, we can prove in this case that all states are recurrent states, so that the chain defines a partition of its state space into finite recurrent communicating classes. We show that our approach is a decisive departure from Markov models at the sentence level and discuss its relationships with Context Free Grammars. Although the toric grammars we use are closely related to Context Free Grammars, the way we generate the language from the grammar is qualitatively different. Our communication model has two purposes. On the one hand, it is used to define indirectly the probability distribution of a random sentence of the language. On the other hand it can serve as a (crude) model of language transmission from one speaker to another speaker through the communication of a (large) set of sentences.

Risk bounds in linear regression through PAC-Bayesian truncation

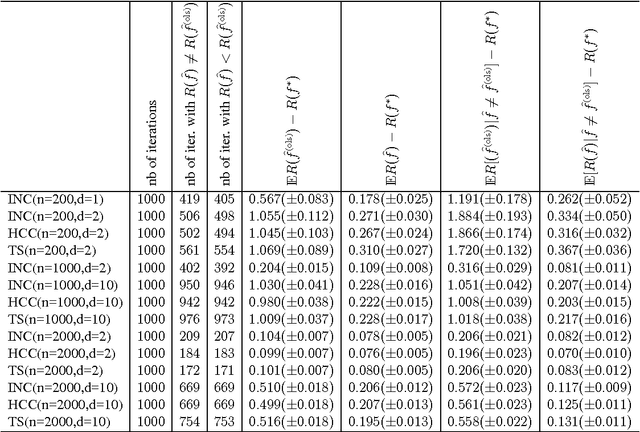
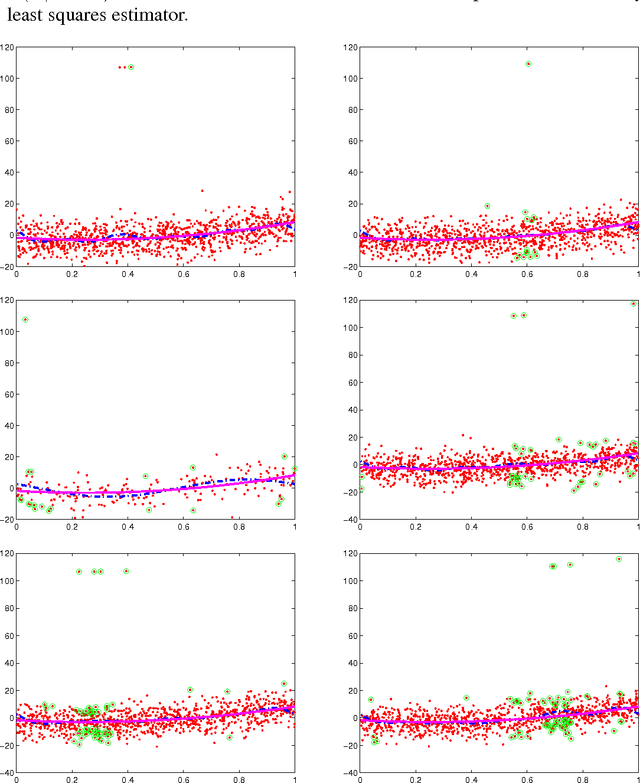
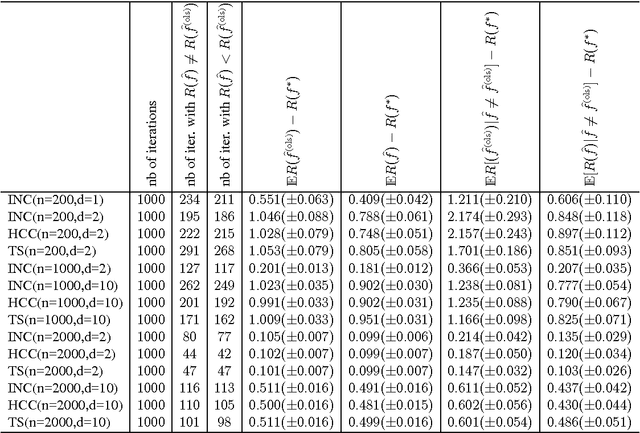
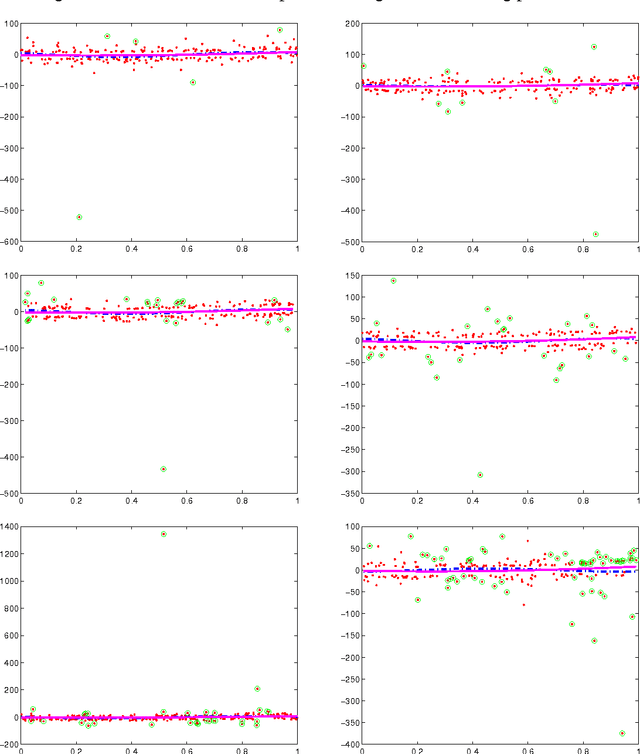
We consider the problem of predicting as well as the best linear combination of d given functions in least squares regression, and variants of this problem including constraints on the parameters of the linear combination. When the input distribution is known, there already exists an algorithm having an expected excess risk of order d/n, where n is the size of the training data. Without this strong assumption, standard results often contain a multiplicative log n factor, and require some additional assumptions like uniform boundedness of the d-dimensional input representation and exponential moments of the output. This work provides new risk bounds for the ridge estimator and the ordinary least squares estimator, and their variants. It also provides shrinkage procedures with convergence rate d/n (i.e., without the logarithmic factor) in expectation and in deviations, under various assumptions. The key common surprising factor of these results is the absence of exponential moment condition on the output distribution while achieving exponential deviations. All risk bounds are obtained through a PAC-Bayesian analysis on truncated differences of losses. Finally, we show that some of these results are not particular to the least squares loss, but can be generalized to similar strongly convex loss functions.

Pac-Bayesian Supervised Classification: The Thermodynamics of Statistical Learning

This monograph deals with adaptive supervised classification, using tools borrowed from statistical mechanics and information theory, stemming from the PACBayesian approach pioneered by David McAllester and applied to a conception of statistical learning theory forged by Vladimir Vapnik. Using convex analysis on the set of posterior probability measures, we show how to get local measures of the complexity of the classification model involving the relative entropy of posterior distributions with respect to Gibbs posterior measures. We then discuss relative bounds, comparing the generalization error of two classification rules, showing how the margin assumption of Mammen and Tsybakov can be replaced with some empirical measure of the covariance structure of the classification model.We show how to associate to any posterior distribution an effective temperature relating it to the Gibbs prior distribution with the same level of expected error rate, and how to estimate this effective temperature from data, resulting in an estimator whose expected error rate converges according to the best possible power of the sample size adaptively under any margin and parametric complexity assumptions. We describe and study an alternative selection scheme based on relative bounds between estimators, and present a two step localization technique which can handle the selection of a parametric model from a family of those. We show how to extend systematically all the results obtained in the inductive setting to transductive learning, and use this to improve Vapnik's generalization bounds, extending them to the case when the sample is made of independent non-identically distributed pairs of patterns and labels. Finally we review briefly the construction of Support Vector Machines and show how to derive generalization bounds for them, measuring the complexity either through the number of support vectors or through the value of the transductive or inductive margin.