Physics of Language Models: Part 2.2, How to Learn From Mistakes on Grade-School Math Problems

Language models have demonstrated remarkable performance in solving reasoning tasks; however, even the strongest models still occasionally make reasoning mistakes. Recently, there has been active research aimed at improving reasoning accuracy, particularly by using pretrained language models to "self-correct" their mistakes via multi-round prompting. In this paper, we follow this line of work but focus on understanding the usefulness of incorporating "error-correction" data directly into the pretraining stage. This data consists of erroneous solution steps immediately followed by their corrections. Using a synthetic math dataset, we show promising results: this type of pretrain data can help language models achieve higher reasoning accuracy directly (i.e., through simple auto-regression, without multi-round prompting) compared to pretraining on the same amount of error-free data. We also delve into many details, such as (1) how this approach differs from beam search, (2) how such data can be prepared, (3) whether masking is needed on the erroneous tokens, (4) the amount of error required, (5) whether such data can be deferred to the fine-tuning stage, and many others.

Physics of Language Models: Part 2.1, Grade-School Math and the Hidden Reasoning Process

Recent advances in language models have demonstrated their capability to solve mathematical reasoning problems, achieving near-perfect accuracy on grade-school level math benchmarks like GSM8K. In this paper, we formally study how language models solve these problems. We design a series of controlled experiments to address several fundamental questions: (1) Can language models truly develop reasoning skills, or do they simply memorize templates? (2) What is the model's hidden (mental) reasoning process? (3) Do models solve math questions using skills similar to or different from humans? (4) Do models trained on GSM8K-like datasets develop reasoning skills beyond those necessary for solving GSM8K problems? (5) What mental process causes models to make reasoning mistakes? (6) How large or deep must a model be to effectively solve GSM8K-level math questions? Our study uncovers many hidden mechanisms by which language models solve mathematical questions, providing insights that extend beyond current understandings of LLMs.

Physics of Language Models: Part 3.3, Knowledge Capacity Scaling Laws

Scaling laws describe the relationship between the size of language models and their capabilities. Unlike prior studies that evaluate a model's capability via loss or benchmarks, we estimate the number of knowledge bits a model stores. We focus on factual knowledge represented as tuples, such as (USA, capital, Washington D.C.) from a Wikipedia page. Through multiple controlled datasets, we establish that language models can and only can store 2 bits of knowledge per parameter, even when quantized to int8, and such knowledge can be flexibly extracted for downstream applications. Consequently, a 7B model can store 14B bits of knowledge, surpassing the English Wikipedia and textbooks combined based on our estimation. More broadly, we present 12 results on how (1) training duration, (2) model architecture, (3) quantization, (4) sparsity constraints such as MoE, and (5) data signal-to-noise ratio affect a model's knowledge storage capacity. Notable insights include: * The GPT-2 architecture, with rotary embedding, matches or even surpasses LLaMA/Mistral architectures in knowledge storage, particularly over shorter training durations. This arises because LLaMA/Mistral uses GatedMLP, which is less stable and harder to train. * Prepending training data with domain names (e.g., wikipedia.org) significantly increases a model's knowledge capacity. Language models can autonomously identify and prioritize domains rich in knowledge, optimizing their storage capacity.

Reverse Training to Nurse the Reversal Curse

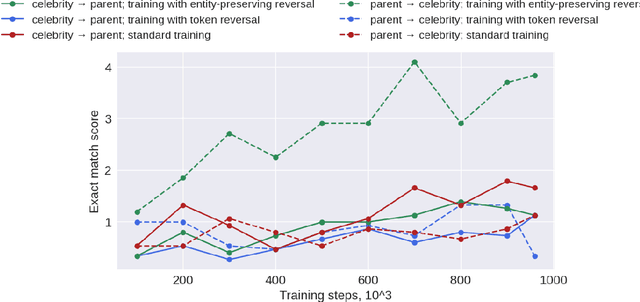
Large language models (LLMs) have a surprising failure: when trained on "A has a feature B", they do not generalize to "B is a feature of A", which is termed the Reversal Curse. Even when training with trillions of tokens this issue still appears due to Zipf's law - hence even if we train on the entire internet. This work proposes an alternative training scheme, called reverse training, whereby all words are used twice, doubling the amount of available tokens. The LLM is trained in both forward and reverse directions by reversing the training strings while preserving (i.e., not reversing) chosen substrings, such as entities. We show that data-matched reverse-trained models provide superior performance to standard models on standard tasks, and compute-matched reverse-trained models provide far superior performance on reversal tasks, helping resolve the reversal curse issue.

Physics of Language Models: Part 3.2, Knowledge Manipulation

Language models can store vast amounts of factual knowledge, but their ability to use this knowledge for logical reasoning remains questionable. This paper explores a language model's ability to manipulate its stored knowledge during inference. We focus on four manipulation types: retrieval (e.g., "What is person A's attribute X"), classification (e.g., "Is A's attribute X even or odd?"), comparison (e.g., "Is A greater than B in attribute X?") and inverse search (e.g., "Which person's attribute X equals T?") We observe that pre-trained language models like GPT2/3/4 excel in knowledge retrieval but struggle with simple classification or comparison tasks unless Chain of Thoughts (CoTs) are employed during both training and inference. They also perform poorly in inverse knowledge search, irrespective of the prompts. Our primary contribution is a synthetic dataset for a controlled experiment that confirms these inherent weaknesses: a language model cannot efficiently manipulate knowledge from pre-training data, even when such knowledge is perfectly stored and fully extractable in the models, and despite adequate instruct fine-tuning.

Physics of Language Models: Part 1, Context-Free Grammar

We design experiments to study $\textit{how}$ generative language models, like GPT, learn context-free grammars (CFGs) -- diverse language systems with a tree-like structure capturing many aspects of natural languages, programs, and human logics. CFGs are as hard as pushdown automata, and can be ambiguous so that verifying if a string satisfies the rules requires dynamic programming. We construct synthetic data and demonstrate that even for very challenging CFGs, pre-trained transformers can learn to generate sentences with near-perfect accuracy and remarkable $\textit{diversity}$. More importantly, we delve into the $\textit{physical principles}$ behind how transformers learns CFGs. We discover that the hidden states within the transformer implicitly and $\textit{precisely}$ encode the CFG structure (such as putting tree node information exactly on the subtree boundary), and learn to form "boundary to boundary" attentions that resemble dynamic programming. We also cover some extension of CFGs as well as the robustness aspect of transformers against grammar mistakes. Overall, our research provides a comprehensive and empirical understanding of how transformers learn CFGs, and reveals the physical mechanisms utilized by transformers to capture the structure and rules of languages.

LoRA: Low-Rank Adaptation of Large Language Models

The dominant paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, conventional fine-tuning, which retrains all model parameters, becomes less feasible. Using GPT-3 175B as an example, deploying many independent instances of fine-tuned models, each with 175B parameters, is extremely expensive. We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks. For GPT-3, LoRA can reduce the number of trainable parameters by 10,000 times and the computation hardware requirement by 3 times compared to full fine-tuning. LoRA performs on-par or better than fine-tuning in model quality on both GPT-3 and GPT-2, despite having fewer trainable parameters, a higher training throughput, and no additional inference latency. We also provide an empirical investigation into rank-deficiency in language model adaptations, which sheds light on the efficacy of LoRA. We release our implementation in GPT-2 at https://github.com/microsoft/LoRA .

Forward Super-Resolution: How Can GANs Learn Hierarchical Generative Models for Real-World Distributions

Generative adversarial networks (GANs) are among the most successful models for learning high-complexity, real-world distributions. However, in theory, due to the highly non-convex, non-concave landscape of the minmax training objective, GAN remains one of the least understood deep learning models. In this work, we formally study how GANs can efficiently learn certain hierarchically generated distributions that are close to the distribution of images in practice. We prove that when a distribution has a structure that we refer to as Forward Super-Resolution, then simply training generative adversarial networks using gradient descent ascent (GDA) can indeed learn this distribution efficiently, both in terms of sample and time complexities. We also provide concrete empirical evidence that not only our assumption "forward super-resolution" is very natural in practice, but also the underlying learning mechanisms that we study in this paper (to allow us efficiently train GAN via GDA in theory) simulates the actual learning process of GANs in practice on real-world problems.

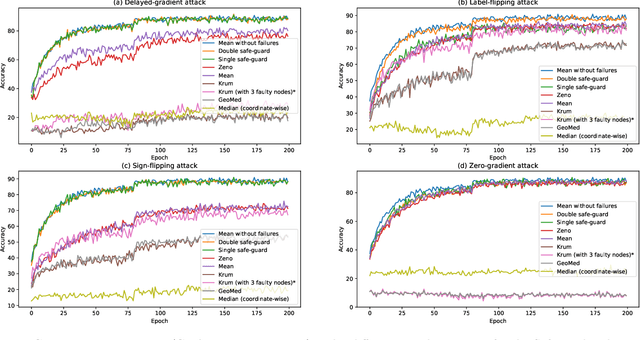
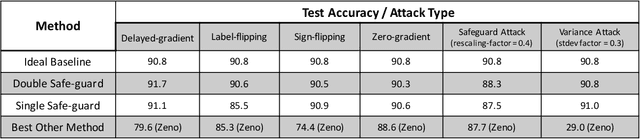
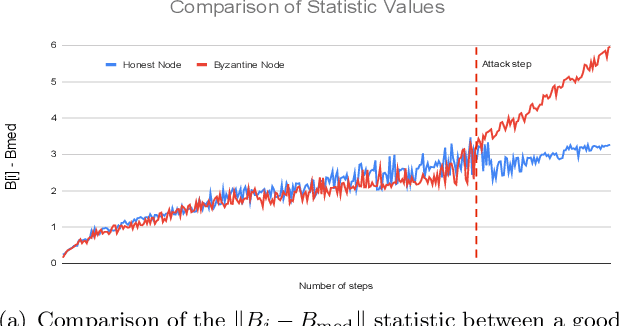
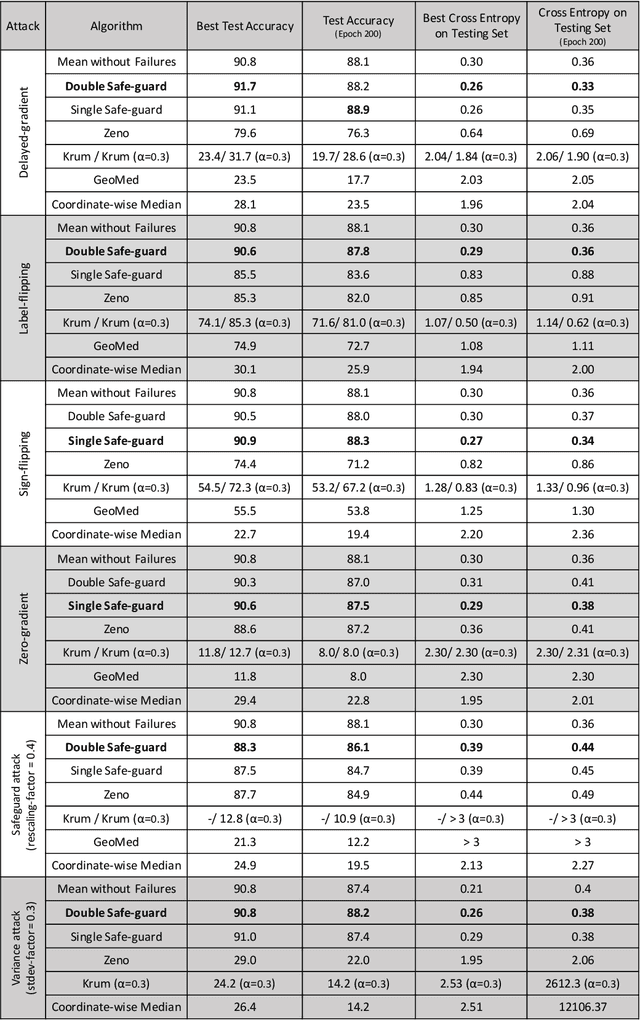
Byzantine-Resilient Non-Convex Stochastic Gradient Descent

We study adversary-resilient stochastic distributed optimization, in which $m$ machines can independently compute stochastic gradients, and cooperate to jointly optimize over their local objective functions. However, an $\alpha$-fraction of the machines are $\textit{Byzantine}$, in that they may behave in arbitrary, adversarial ways. We consider a variant of this procedure in the challenging $\textit{non-convex}$ case. Our main result is a new algorithm SafeguardSGD which can provably escape saddle points and find approximate local minima of the non-convex objective. The algorithm is based on a new concentration filtering technique, and its sample and time complexity bounds match the best known theoretical bounds in the stochastic, distributed setting when no Byzantine machines are present. Our algorithm is practical: it improves upon the performance of prior methods when training deep neural networks, it is relatively lightweight, and is the first method to withstand two recently-proposed Byzantine attacks.

Towards Understanding Ensemble, Knowledge Distillation and Self-Distillation in Deep Learning

We formally study how Ensemble of deep learning models can improve test accuracy, and how the superior performance of ensemble can be distilled into a single model using Knowledge Distillation. We consider the challenging case where the ensemble is simply an average of the outputs of a few independently trained neural networks with the SAME architecture, trained using the SAME algorithm on the SAME data set, and they only differ by the random seeds used in the initialization. We empirically show that ensemble/knowledge distillation in deep learning works very differently from traditional learning theory, especially differently from ensemble of random feature mappings or the neural-tangent-kernel feature mappings, and is potentially out of the scope of existing theorems. Thus, to properly understand ensemble and knowledge distillation in deep learning, we develop a theory showing that when data has a structure we refer to as "multi-view", then ensemble of independently trained neural networks can provably improve test accuracy, and such superior test accuracy can also be provably distilled into a single model by training a single model to match the output of the ensemble instead of the true label. Our result sheds light on how ensemble works in deep learning in a way that is completely different from traditional theorems, and how the "dark knowledge" is hidden in the outputs of the ensemble -- that can be used in knowledge distillation -- comparing to the true data labels. In the end, we prove that self-distillation can also be viewed as implicitly combining ensemble and knowledge distillation to improve test accuracy.