Reinforcement Learning with Backtracking Feedback

Addressing the critical need for robust safety in Large Language Models (LLMs), particularly against adversarial attacks and in-distribution errors, we introduce Reinforcement Learning with Backtracking Feedback (RLBF). This framework advances upon prior methods, such as BSAFE, by primarily leveraging a Reinforcement Learning (RL) stage where models learn to dynamically correct their own generation errors. Through RL with critic feedback on the model's live outputs, LLMs are trained to identify and recover from their actual, emergent safety violations by emitting an efficient "backtrack by x tokens" signal, then continuing generation autoregressively. This RL process is crucial for instilling resilience against sophisticated adversarial strategies, including middle filling, Greedy Coordinate Gradient (GCG) attacks, and decoding parameter manipulations. To further support the acquisition of this backtracking capability, we also propose an enhanced Supervised Fine-Tuning (SFT) data generation strategy (BSAFE+). This method improves upon previous data creation techniques by injecting violations into coherent, originally safe text, providing more effective initial training for the backtracking mechanism. Comprehensive empirical evaluations demonstrate that RLBF significantly reduces attack success rates across diverse benchmarks and model scales, achieving superior safety outcomes while critically preserving foundational model utility.

CausalArmor: Efficient Indirect Prompt Injection Guardrails via Causal Attribution

AI agents equipped with tool-calling capabilities are susceptible to Indirect Prompt Injection (IPI) attacks. In this attack scenario, malicious commands hidden within untrusted content trick the agent into performing unauthorized actions. Existing defenses can reduce attack success but often suffer from the over-defense dilemma: they deploy expensive, always-on sanitization regardless of actual threat, thereby degrading utility and latency even in benign scenarios. We revisit IPI through a causal ablation perspective: a successful injection manifests as a dominance shift where the user request no longer provides decisive support for the agent's privileged action, while a particular untrusted segment, such as a retrieved document or tool output, provides disproportionate attributable influence. Based on this signature, we propose CausalArmor, a selective defense framework that (i) computes lightweight, leave-one-out ablation-based attributions at privileged decision points, and (ii) triggers targeted sanitization only when an untrusted segment dominates the user intent. Additionally, CausalArmor employs retroactive Chain-of-Thought masking to prevent the agent from acting on ``poisoned'' reasoning traces. We present a theoretical analysis showing that sanitization based on attribution margins conditionally yields an exponentially small upper bound on the probability of selecting malicious actions. Experiments on AgentDojo and DoomArena demonstrate that CausalArmor matches the security of aggressive defenses while improving explainability and preserving utility and latency of AI agents.

Backtracking for Safety

Large language models (LLMs) have demonstrated remarkable capabilities across various tasks, but ensuring their safety and alignment with human values remains crucial. Current safety alignment methods, such as supervised fine-tuning and reinforcement learning-based approaches, can exhibit vulnerabilities to adversarial attacks and often result in shallow safety alignment, primarily focusing on preventing harmful content in the initial tokens of the generated output. While methods like resetting can help recover from unsafe generations by discarding previous tokens and restarting the generation process, they are not well-suited for addressing nuanced safety violations like toxicity that may arise within otherwise benign and lengthy generations. In this paper, we propose a novel backtracking method designed to address these limitations. Our method allows the model to revert to a safer generation state, not necessarily at the beginning, when safety violations occur during generation. This approach enables targeted correction of problematic segments without discarding the entire generated text, thereby preserving efficiency. We demonstrate that our method dramatically reduces toxicity appearing through the generation process with minimal impact to efficiency.

LoRA: Low-Rank Adaptation of Large Language Models

The dominant paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, conventional fine-tuning, which retrains all model parameters, becomes less feasible. Using GPT-3 175B as an example, deploying many independent instances of fine-tuned models, each with 175B parameters, is extremely expensive. We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks. For GPT-3, LoRA can reduce the number of trainable parameters by 10,000 times and the computation hardware requirement by 3 times compared to full fine-tuning. LoRA performs on-par or better than fine-tuning in model quality on both GPT-3 and GPT-2, despite having fewer trainable parameters, a higher training throughput, and no additional inference latency. We also provide an empirical investigation into rank-deficiency in language model adaptations, which sheds light on the efficacy of LoRA. We release our implementation in GPT-2 at https://github.com/microsoft/LoRA .

Differential Equation Units: Learning Functional Forms of Activation Functions from Data

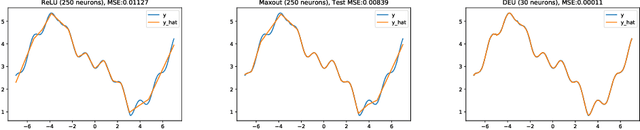
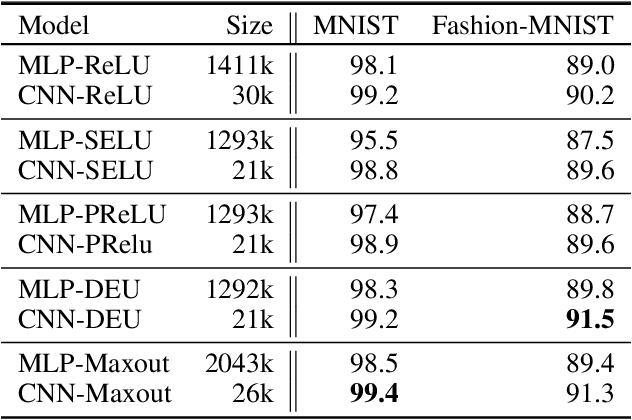
Most deep neural networks use simple, fixed activation functions, such as sigmoids or rectified linear units, regardless of domain or network structure. We introduce differential equation units (DEUs), an improvement to modern neural networks, which enables each neuron to learn a particular nonlinear activation function from a family of solutions to an ordinary differential equation. Specifically, each neuron may change its functional form during training based on the behavior of the other parts of the network. We show that using neurons with DEU activation functions results in a more compact network capable of achieving comparable, if not superior, performance when is compared to much larger networks.

Learning Compact Neural Networks Using Ordinary Differential Equations as Activation Functions

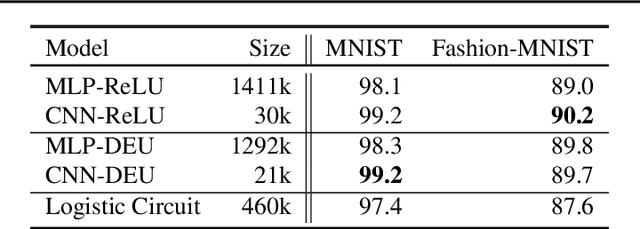
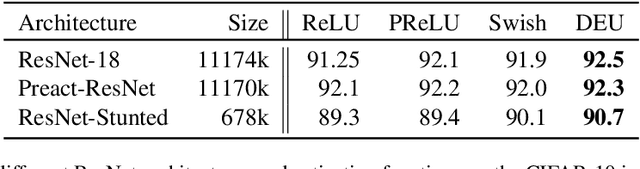
Most deep neural networks use simple, fixed activation functions, such as sigmoids or rectified linear units, regardless of domain or network structure. We introduce differential equation units (DEUs), an improvement to modern neural networks, which enables each neuron to learn a particular nonlinear activation function from a family of solutions to an ordinary differential equation. Specifically, each neuron may change its functional form during training based on the behavior of the other parts of the network. We show that using neurons with DEU activation functions results in a more compact network capable of achieving comparable, if not superior, performance when is compared to much larger networks.