TGTOD: A Global Temporal Graph Transformer for Outlier Detection at Scale

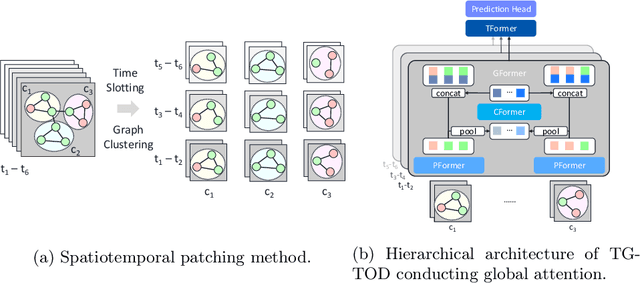
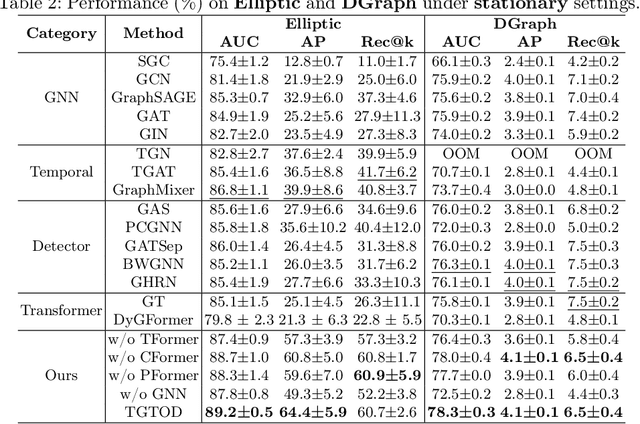
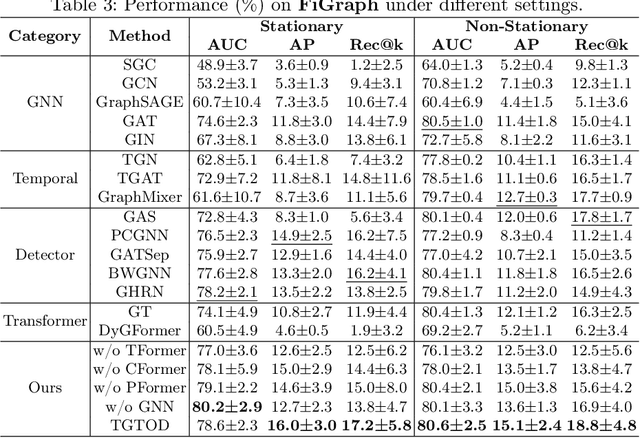
While Transformers have revolutionized machine learning on various data, existing Transformers for temporal graphs face limitations in (1) restricted receptive fields, (2) overhead of subgraph extraction, and (3) suboptimal generalization capability beyond link prediction. In this paper, we rethink temporal graph Transformers and propose TGTOD, a novel end-to-end Temporal Graph Transformer for Outlier Detection. TGTOD employs global attention to model both structural and temporal dependencies within temporal graphs. To tackle scalability, our approach divides large temporal graphs into spatiotemporal patches, which are then processed by a hierarchical Transformer architecture comprising Patch Transformer, Cluster Transformer, and Temporal Transformer. We evaluate TGTOD on three public datasets under two settings, comparing with a wide range of baselines. Our experimental results demonstrate the effectiveness of TGTOD, achieving AP improvement of 61% on Elliptic. Furthermore, our efficiency evaluation shows that TGTOD reduces training time by 44x compared to existing Transformers for temporal graphs. To foster reproducibility, we make our implementation publicly available at https://github.com/kayzliu/tgtod.

Robustness Reprogramming for Representation Learning

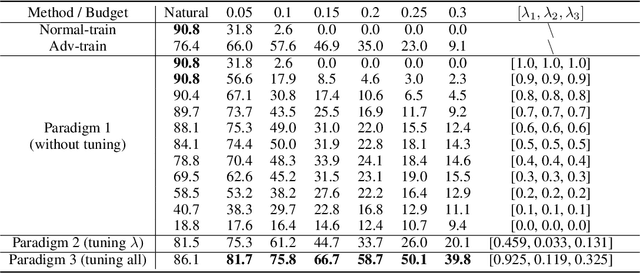
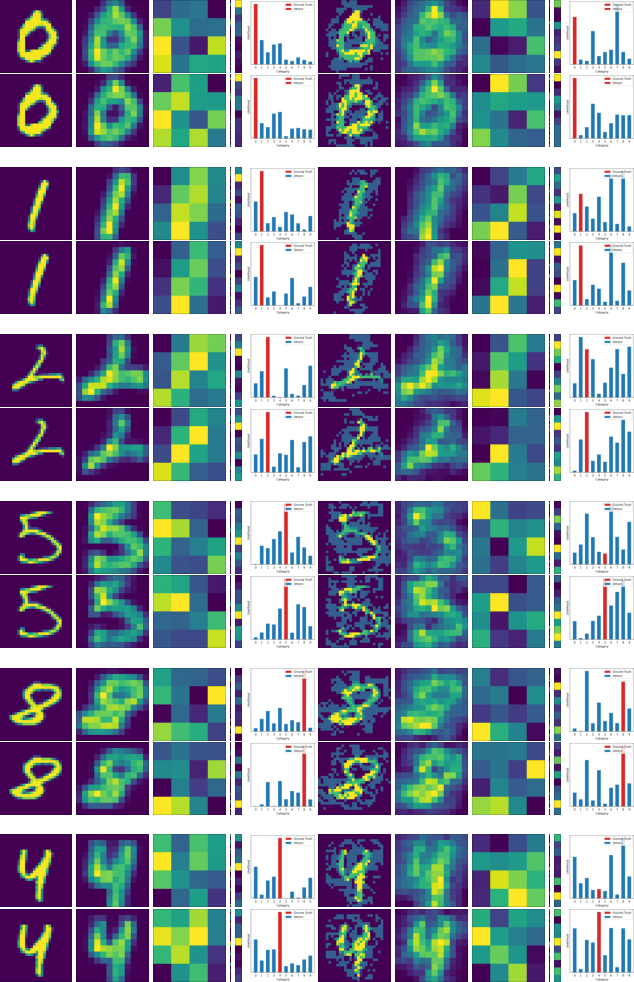
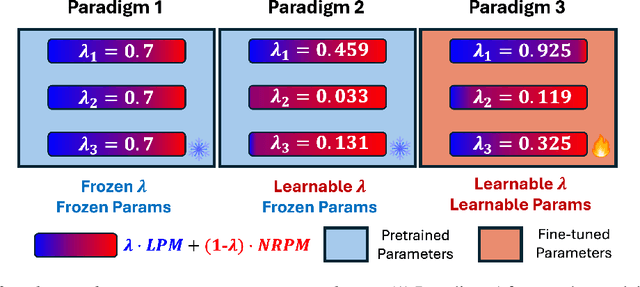
This work tackles an intriguing and fundamental open challenge in representation learning: Given a well-trained deep learning model, can it be reprogrammed to enhance its robustness against adversarial or noisy input perturbations without altering its parameters? To explore this, we revisit the core feature transformation mechanism in representation learning and propose a novel non-linear robust pattern matching technique as a robust alternative. Furthermore, we introduce three model reprogramming paradigms to offer flexible control of robustness under different efficiency requirements. Comprehensive experiments and ablation studies across diverse learning models ranging from basic linear model and MLPs to shallow and modern deep ConvNets demonstrate the effectiveness of our approaches. This work not only opens a promising and orthogonal direction for improving adversarial defenses in deep learning beyond existing methods but also provides new insights into designing more resilient AI systems with robust statistics.

HLogformer: A Hierarchical Transformer for Representing Log Data

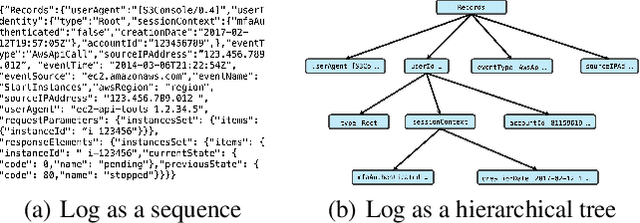
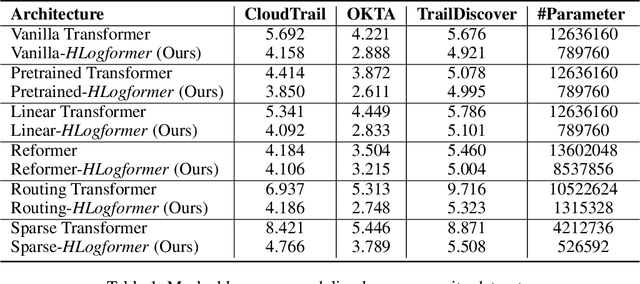
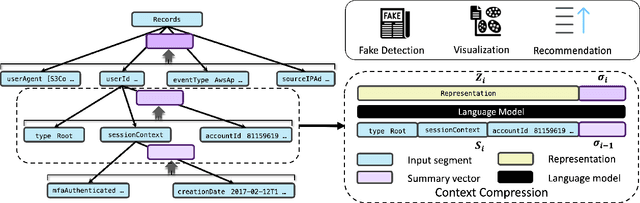
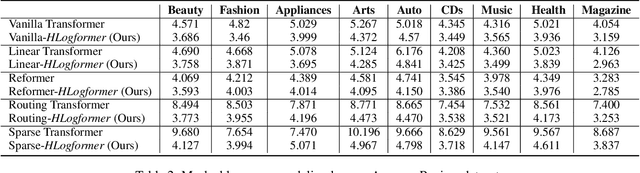
Transformers have gained widespread acclaim for their versatility in handling diverse data structures, yet their application to log data remains underexplored. Log data, characterized by its hierarchical, dictionary-like structure, poses unique challenges when processed using conventional transformer models. Traditional methods often rely on manually crafted templates for parsing logs, a process that is labor-intensive and lacks generalizability. Additionally, the linear treatment of log sequences by standard transformers neglects the rich, nested relationships within log entries, leading to suboptimal representations and excessive memory usage. To address these issues, we introduce HLogformer, a novel hierarchical transformer framework specifically designed for log data. HLogformer leverages the hierarchical structure of log entries to significantly reduce memory costs and enhance representation learning. Unlike traditional models that treat log data as flat sequences, our framework processes log entries in a manner that respects their inherent hierarchical organization. This approach ensures comprehensive encoding of both fine-grained details and broader contextual relationships. Our contributions are threefold: First, HLogformer is the first framework to design a dynamic hierarchical transformer tailored for dictionary-like log data. Second, it dramatically reduces memory costs associated with processing extensive log sequences. Third, comprehensive experiments demonstrate that HLogformer more effectively encodes hierarchical contextual information, proving to be highly effective for downstream tasks such as synthetic anomaly detection and product recommendation.

Towards Label Position Bias in Graph Neural Networks

Graph Neural Networks (GNNs) have emerged as a powerful tool for semi-supervised node classification tasks. However, recent studies have revealed various biases in GNNs stemming from both node features and graph topology. In this work, we uncover a new bias - label position bias, which indicates that the node closer to the labeled nodes tends to perform better. We introduce a new metric, the Label Proximity Score, to quantify this bias, and find that it is closely related to performance disparities. To address the label position bias, we propose a novel optimization framework for learning a label position unbiased graph structure, which can be applied to existing GNNs. Extensive experiments demonstrate that our proposed method not only outperforms backbone methods but also significantly mitigates the issue of label position bias in GNNs.

LazyGNN: Large-Scale Graph Neural Networks via Lazy Propagation

Recent works have demonstrated the benefits of capturing long-distance dependency in graphs by deeper graph neural networks (GNNs). But deeper GNNs suffer from the long-lasting scalability challenge due to the neighborhood explosion problem in large-scale graphs. In this work, we propose to capture long-distance dependency in graphs by shallower models instead of deeper models, which leads to a much more efficient model, LazyGNN, for graph representation learning. Moreover, we demonstrate that LazyGNN is compatible with existing scalable approaches (such as sampling methods) for further accelerations through the development of mini-batch LazyGNN. Comprehensive experiments demonstrate its superior prediction performance and scalability on large-scale benchmarks. LazyGNN also achieves state-of-art performance on the OGB leaderboard.

Differential Equation Units: Learning Functional Forms of Activation Functions from Data

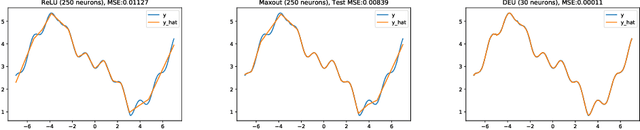
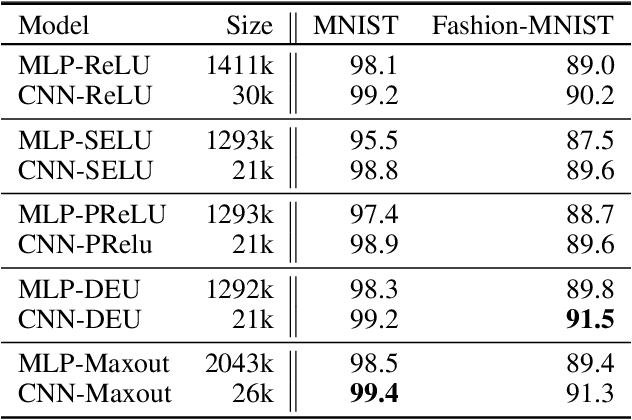
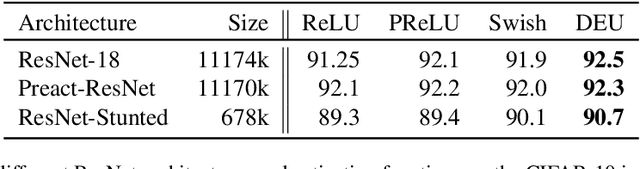
Most deep neural networks use simple, fixed activation functions, such as sigmoids or rectified linear units, regardless of domain or network structure. We introduce differential equation units (DEUs), an improvement to modern neural networks, which enables each neuron to learn a particular nonlinear activation function from a family of solutions to an ordinary differential equation. Specifically, each neuron may change its functional form during training based on the behavior of the other parts of the network. We show that using neurons with DEU activation functions results in a more compact network capable of achieving comparable, if not superior, performance when is compared to much larger networks.

Learning Compact Neural Networks Using Ordinary Differential Equations as Activation Functions

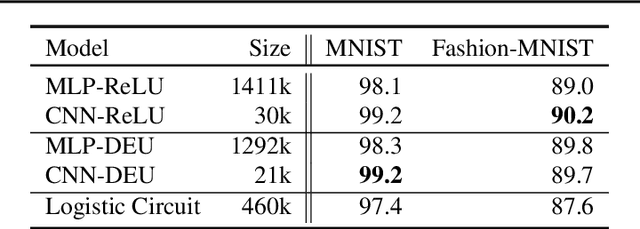
Most deep neural networks use simple, fixed activation functions, such as sigmoids or rectified linear units, regardless of domain or network structure. We introduce differential equation units (DEUs), an improvement to modern neural networks, which enables each neuron to learn a particular nonlinear activation function from a family of solutions to an ordinary differential equation. Specifically, each neuron may change its functional form during training based on the behavior of the other parts of the network. We show that using neurons with DEU activation functions results in a more compact network capable of achieving comparable, if not superior, performance when is compared to much larger networks.