TGTOD: A Global Temporal Graph Transformer for Outlier Detection at Scale

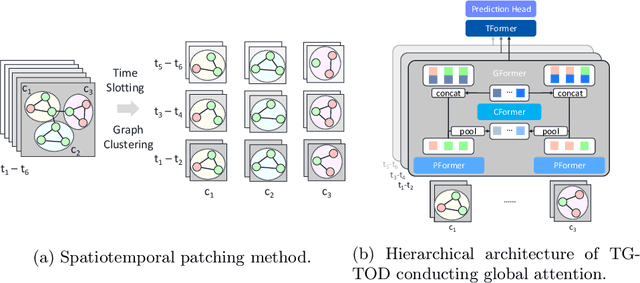
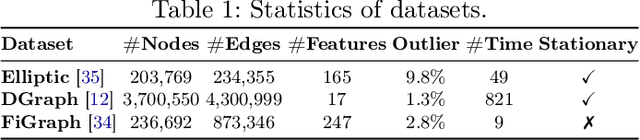
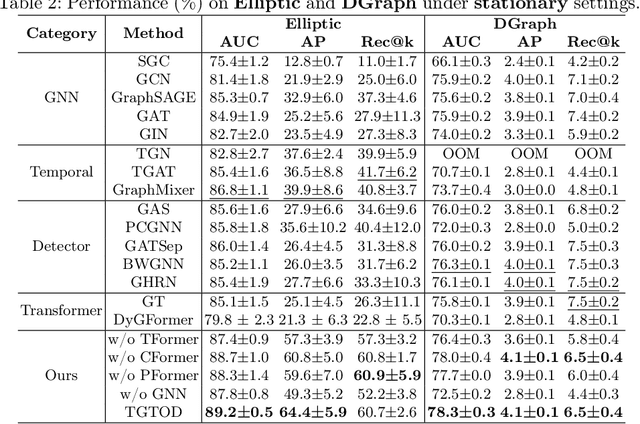
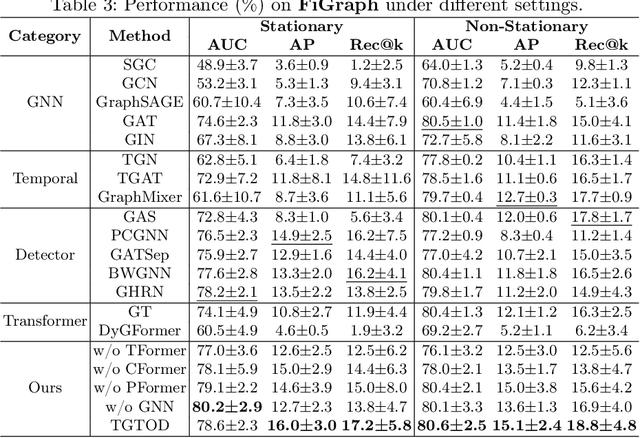
While Transformers have revolutionized machine learning on various data, existing Transformers for temporal graphs face limitations in (1) restricted receptive fields, (2) overhead of subgraph extraction, and (3) suboptimal generalization capability beyond link prediction. In this paper, we rethink temporal graph Transformers and propose TGTOD, a novel end-to-end Temporal Graph Transformer for Outlier Detection. TGTOD employs global attention to model both structural and temporal dependencies within temporal graphs. To tackle scalability, our approach divides large temporal graphs into spatiotemporal patches, which are then processed by a hierarchical Transformer architecture comprising Patch Transformer, Cluster Transformer, and Temporal Transformer. We evaluate TGTOD on three public datasets under two settings, comparing with a wide range of baselines. Our experimental results demonstrate the effectiveness of TGTOD, achieving AP improvement of 61% on Elliptic. Furthermore, our efficiency evaluation shows that TGTOD reduces training time by 44x compared to existing Transformers for temporal graphs. To foster reproducibility, we make our implementation publicly available at https://github.com/kayzliu/tgtod.

PMP: Privacy-Aware Matrix Profile against Sensitive Pattern Inference for Time Series

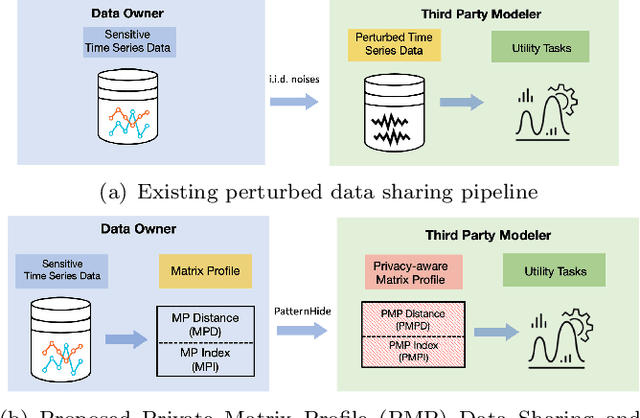
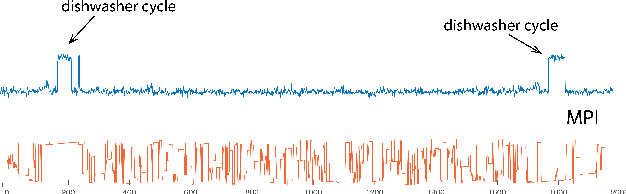
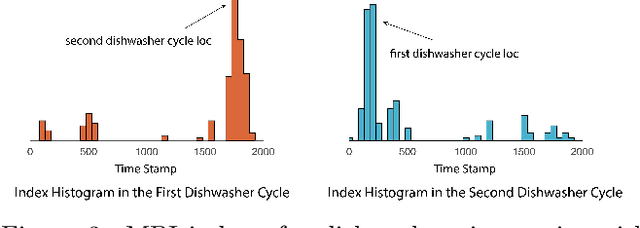
Recent rapid development of sensor technology has allowed massive fine-grained time series (TS) data to be collected and set the foundation for the development of data-driven services and applications. During the process, data sharing is often involved to allow the third-party modelers to perform specific time series data mining (TSDM) tasks based on the need of data owner. The high resolution of TS brings new challenges in protecting privacy. While meaningful information in high-resolution TS shifts from concrete point values to local shape-based segments, numerous research have found that long shape-based patterns could contain more sensitive information and may potentially be extracted and misused by a malicious third party. However, the privacy issue for TS patterns is surprisingly seldom explored in privacy-preserving literature. In this work, we consider a new privacy-preserving problem: preventing malicious inference on long shape-based patterns while preserving short segment information for the utility task performance. To mitigate the challenge, we investigate an alternative approach by sharing Matrix Profile (MP), which is a non-linear transformation of original data and a versatile data structure that supports many data mining tasks. We found that while MP can prevent concrete shape leakage, the canonical correlation in MP index can still reveal the location of sensitive long pattern. Based on this observation, we design two attacks named Location Attack and Entropy Attack to extract the pattern location from MP. To further protect MP from these two attacks, we propose a Privacy-Aware Matrix Profile (PMP) via perturbing the local correlation and breaking the canonical correlation in MP index vector. We evaluate our proposed PMP against baseline noise-adding methods through quantitative analysis and real-world case studies to show the effectiveness of the proposed method.

Towards Fast and Accurate Federated Learning with non-IID Data for Cloud-Based IoT Applications

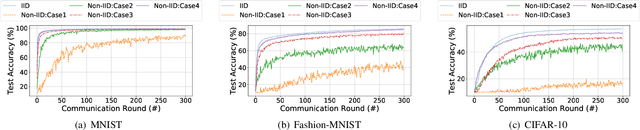
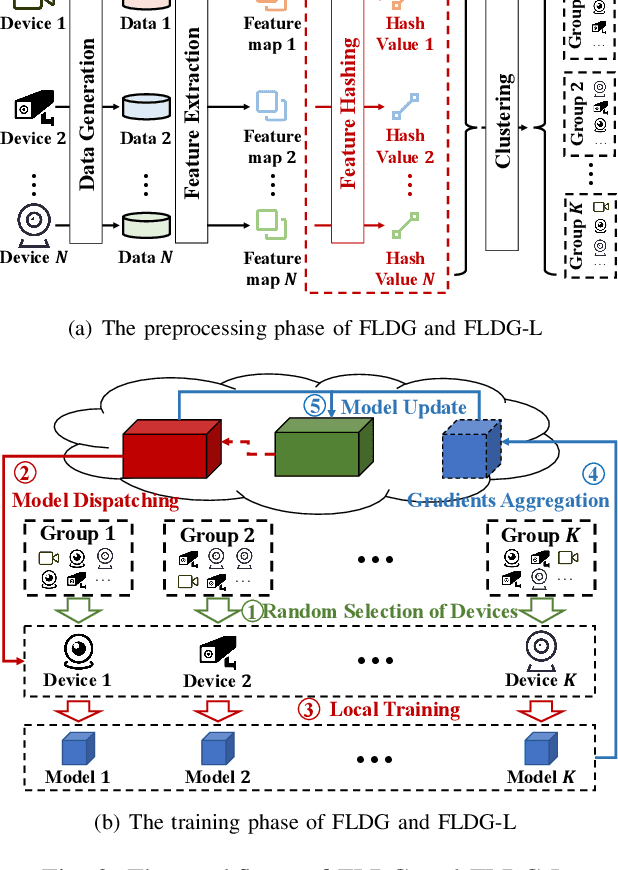
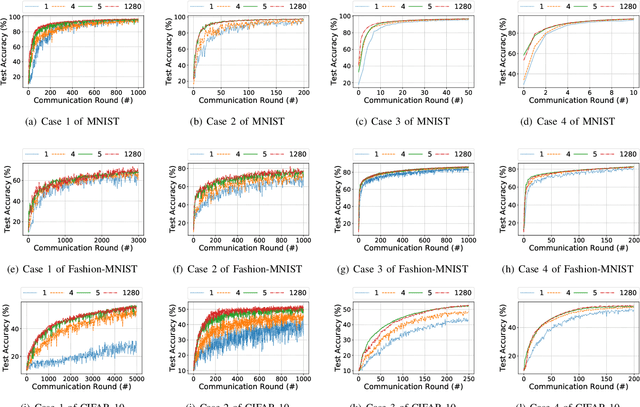
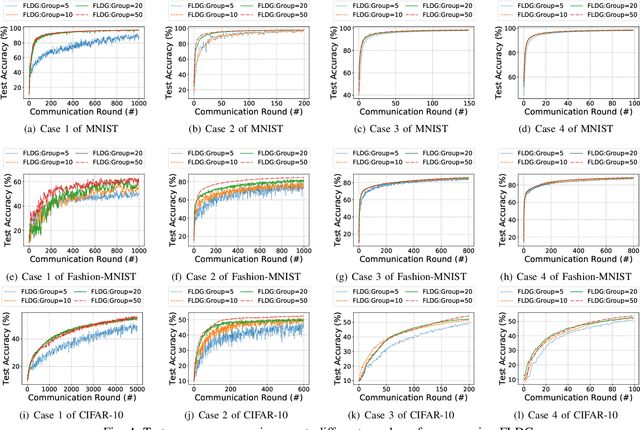
As a promising method of central model training on decentralized device data while securing user privacy, Federated Learning (FL)is becoming popular in Internet of Things (IoT) design. However, when the data collected by IoT devices are highly skewed in a non-independent and identically distributed (non-IID) manner, the accuracy of vanilla FL method cannot be guaranteed. Although there exist various solutions that try to address the bottleneck of FL with non-IID data, most of them suffer from extra intolerable communication overhead and low model accuracy. To enable fast and accurate FL, this paper proposes a novel data-based device grouping approach that can effectively reduce the disadvantages of weight divergence during the training of non-IID data. However, since our grouping method is based on the similarity of extracted feature maps from IoT devices, it may incur additional risks of privacy exposure. To solve this problem, we propose an improved version by exploiting similarity information using the Locality-Sensitive Hashing (LSH) algorithm without exposing extracted feature maps. Comprehensive experimental results on well-known benchmarks show that our approach can not only accelerate the convergence rate, but also improve the prediction accuracy for FL with non-IID data.

To Talk or to Work: Delay Efficient Federated Learning over Mobile Edge Devices

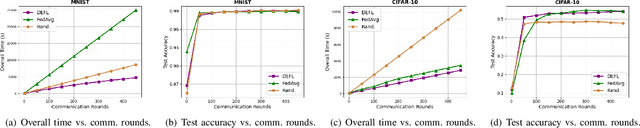
Federated learning (FL), an emerging distributed machine learning paradigm, in conflux with edge computing is a promising area with novel applications over mobile edge devices. In FL, since mobile devices collaborate to train a model based on their own data under the coordination of a central server by sharing just the model updates, training data is maintained private. However, without the central availability of data, computing nodes need to communicate the model updates often to attain convergence. Hence, the local computation time to create local model updates along with the time taken for transmitting them to and from the server result in a delay in the overall time. Furthermore, unreliable network connections may obstruct an efficient communication of these updates. To address these, in this paper, we propose a delay-efficient FL mechanism that reduces the overall time (consisting of both the computation and communication latencies) and communication rounds required for the model to converge. Exploring the impact of various parameters contributing to delay, we seek to balance the trade-off between wireless communication (to talk) and local computation (to work). We formulate a relation with overall time as an optimization problem and demonstrate the efficacy of our approach through extensive simulations.

Evaluation of Inference Attack Models for Deep Learning on Medical Data

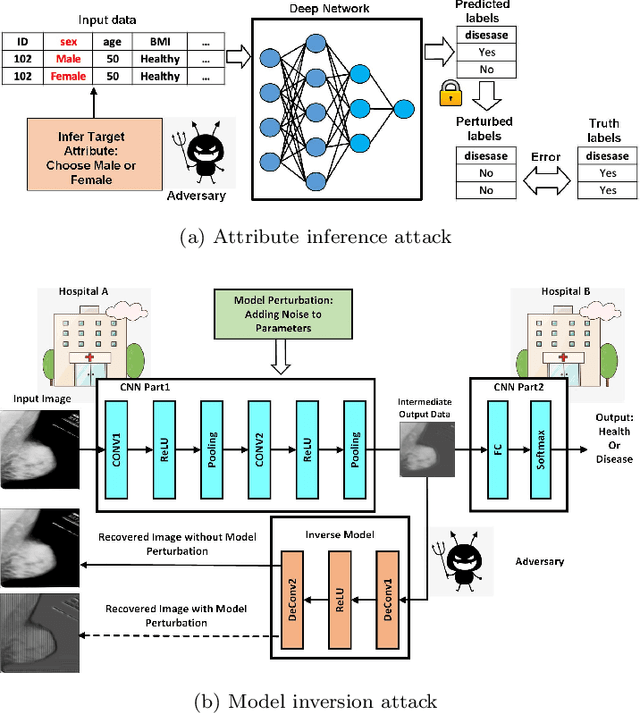
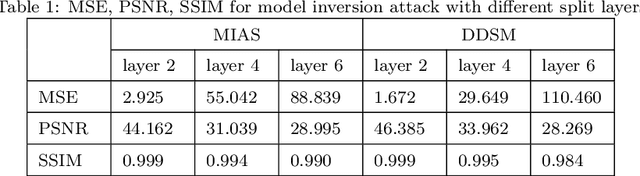
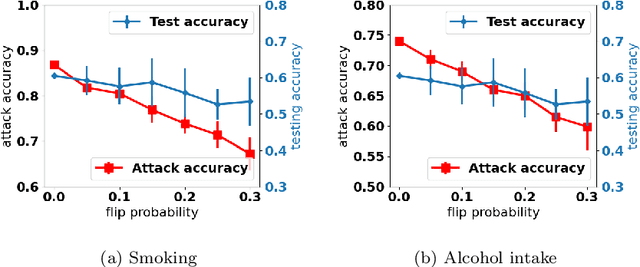
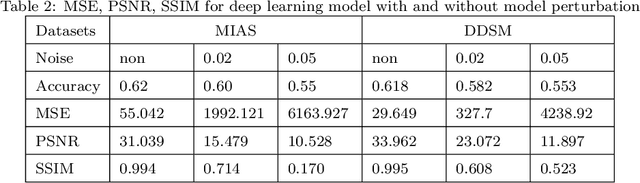
Deep learning has attracted broad interest in healthcare and medical communities. However, there has been little research into the privacy issues created by deep networks trained for medical applications. Recently developed inference attack algorithms indicate that images and text records can be reconstructed by malicious parties that have the ability to query deep networks. This gives rise to the concern that medical images and electronic health records containing sensitive patient information are vulnerable to these attacks. This paper aims to attract interest from researchers in the medical deep learning community to this important problem. We evaluate two prominent inference attack models, namely, attribute inference attack and model inversion attack. We show that they can reconstruct real-world medical images and clinical reports with high fidelity. We then investigate how to protect patients' privacy using defense mechanisms, such as label perturbation and model perturbation. We provide a comparison of attack results between the original and the medical deep learning models with defenses. The experimental evaluations show that our proposed defense approaches can effectively reduce the potential privacy leakage of medical deep learning from the inference attacks.

Differentially Private (Gradient) Expectation Maximization Algorithm with Statistical Guarantees

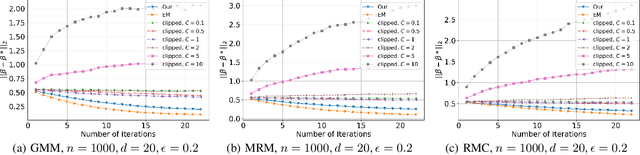
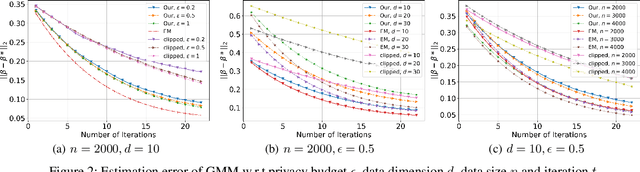
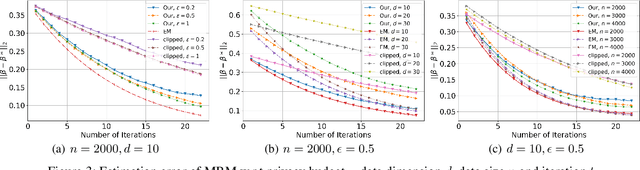
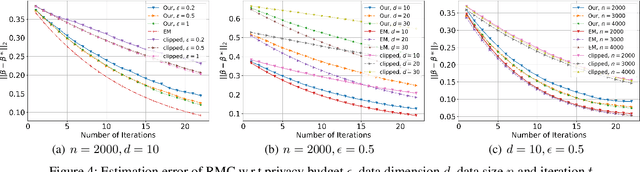
(Gradient) Expectation Maximization (EM) is a widely used algorithm for estimating the maximum likelihood of mixture models or incomplete data problems. A major challenge facing this popular technique is how to effectively preserve the privacy of sensitive data. Previous research on this problem has already lead to the discovery of some Differentially Private (DP) algorithms for (Gradient) EM. However, unlike in the non-private case, existing techniques are not yet able to provide finite sample statistical guarantees. To address this issue, we propose in this paper the first DP version of (Gradient) EM algorithm with statistical guarantees. Moreover, we apply our general framework to three canonical models: Gaussian Mixture Model (GMM), Mixture of Regressions Model (MRM) and Linear Regression with Missing Covariates (RMC). Specifically, for GMM in the DP model, our estimation error is near optimal in some cases. For the other two models, we provide the first finite sample statistical guarantees. Our theory is supported by thorough numerical experiments.

Effective Proximal Methods for Non-convex Non-smooth Regularized Learning

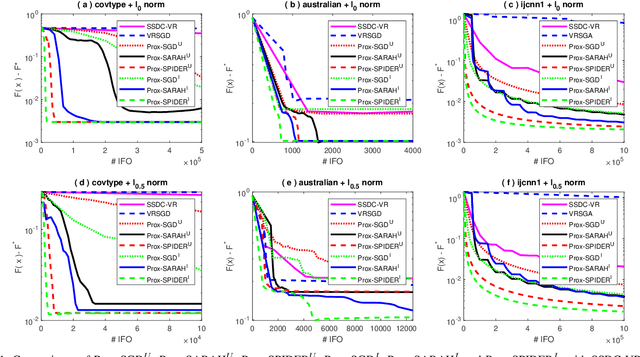
Sparse learning is a very important tool for mining useful information and patterns from high dimensional data. Non-convex non-smooth regularized learning problems play essential roles in sparse learning, and have drawn extensive attentions recently. We design a family of stochastic proximal gradient methods by applying arbitrary sampling to solve the empirical risk minimization problem with a non-convex and non-smooth regularizer. These methods draw mini-batches of training examples according to an arbitrary probability distribution when computing stochastic gradients. A unified analytic approach is developed to examine the convergence and computational complexity of these methods, allowing us to compare the different sampling schemes. We show that the independent sampling scheme tends to improve performance over the commonly-used uniform sampling scheme. Our new analysis also derives a tighter bound on convergence speed for the uniform sampling than the best one available so far. Empirical evaluations demonstrate that the proposed algorithms converge faster than the state of the art.

Towards Plausible Differentially Private ADMM Based Distributed Machine Learning

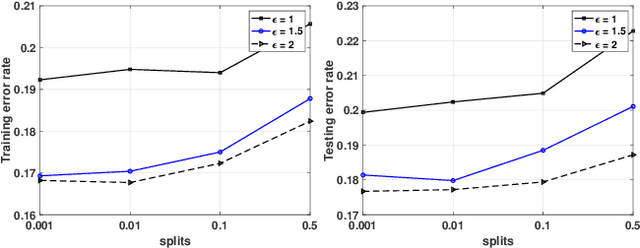
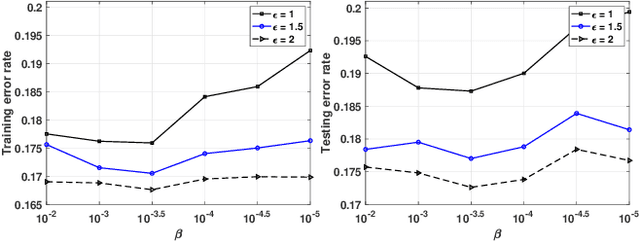
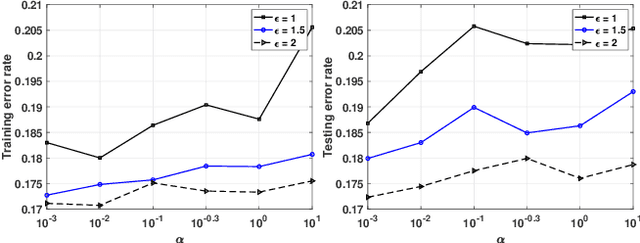
The Alternating Direction Method of Multipliers (ADMM) and its distributed version have been widely used in machine learning. In the iterations of ADMM, model updates using local private data and model exchanges among agents impose critical privacy concerns. Despite some pioneering works to relieve such concerns, differentially private ADMM still confronts many research challenges. For example, the guarantee of differential privacy (DP) relies on the premise that the optimality of each local problem can be perfectly attained in each ADMM iteration, which may never happen in practice. The model trained by DP ADMM may have low prediction accuracy. In this paper, we address these concerns by proposing a novel (Improved) Plausible differentially Private ADMM algorithm, called PP-ADMM and IPP-ADMM. In PP-ADMM, each agent approximately solves a perturbed optimization problem that is formulated from its local private data in an iteration, and then perturbs the approximate solution with Gaussian noise to provide the DP guarantee. To further improve the model accuracy and convergence, an improved version IPP-ADMM adopts sparse vector technique (SVT) to determine if an agent should update its neighbors with the current perturbed solution. The agent calculates the difference of the current solution from that in the last iteration, and if the difference is larger than a threshold, it passes the solution to neighbors; or otherwise the solution will be discarded. Moreover, we propose to track the total privacy loss under the zero-concentrated DP (zCDP) and provide a generalization performance analysis. Experiments on real-world datasets demonstrate that under the same privacy guarantee, the proposed algorithms are superior to the state of the art in terms of model accuracy and convergence rate.

Differentially Private and Fair Classification via Calibrated Functional Mechanism

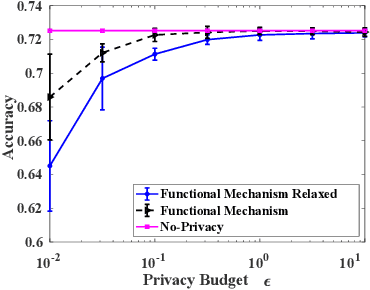
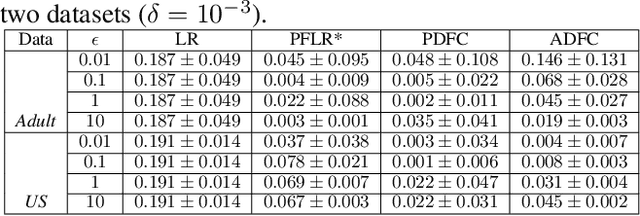
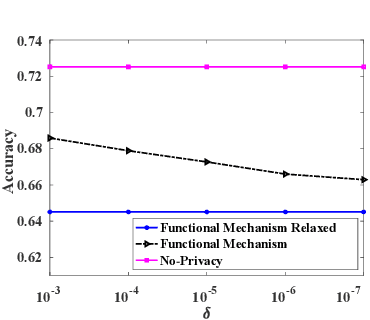
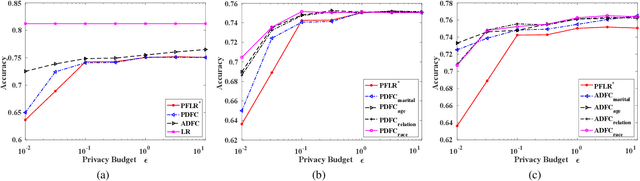
Machine learning is increasingly becoming a powerful tool to make decisions in a wide variety of applications, such as medical diagnosis and autonomous driving. Privacy concerns related to the training data and unfair behaviors of some decisions with regard to certain attributes (e.g., sex, race) are becoming more critical. Thus, constructing a fair machine learning model while simultaneously providing privacy protection becomes a challenging problem. In this paper, we focus on the design of classification model with fairness and differential privacy guarantees by jointly combining functional mechanism and decision boundary fairness. In order to enforce $\epsilon$-differential privacy and fairness, we leverage the functional mechanism to add different amounts of Laplace noise regarding different attributes to the polynomial coefficients of the objective function in consideration of fairness constraint. We further propose an utility-enhancement scheme, called relaxed functional mechanism by adding Gaussian noise instead of Laplace noise, hence achieving $(\epsilon,\delta)$-differential privacy. Based on the relaxed functional mechanism, we can design $(\epsilon,\delta)$-differentially private and fair classification model. Moreover, our theoretical analysis and empirical results demonstrate that our two approaches achieve both fairness and differential privacy while preserving good utility and outperform the state-of-the-art algorithms.

Optimal Differentially Private ADMM for Distributed Machine Learning

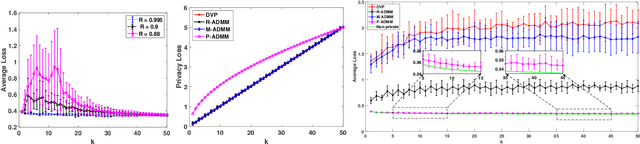
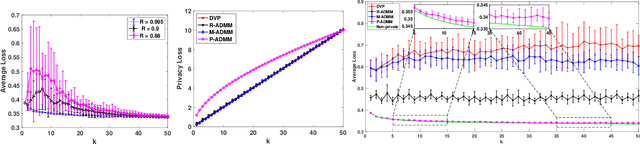
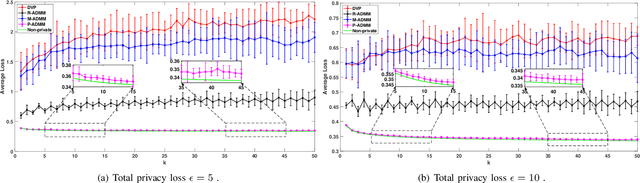
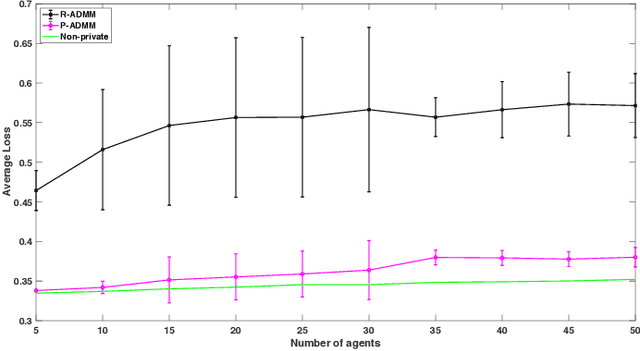
Due to massive amounts of data distributed across multiple locations, distributed machine learning has attracted a lot of research interests. Alternating Direction Method of Multipliers (ADMM) is a powerful method of designing distributed machine learning algorithm, whereby each agent computes over local datasets and exchanges computation results with its neighbor agents in an iterative procedure. There exists significant privacy leakage during this iterative process if the local data is sensitive. In this paper, we propose a differentially private ADMM algorithm (P-ADMM) to provide dynamic zero-concentrated differential privacy (dynamic zCDP), by inserting Gaussian noise with linearly decaying variance. We prove that P-ADMM has the same convergence rate compared to the non-private counterpart, i.e., $\mathcal{O}(1/K)$ with $K$ being the number of iterations and linear convergence for general convex and strongly convex problems while providing differentially private guarantee. Moreover, through our experiments performed on real-world datasets, we empirically show that P-ADMM has the best-known performance among the existing differentially private ADMM based algorithms.