Stochastic Variance-Reduced Iterative Hard Thresholding in Graph Sparsity Optimization

Stochastic optimization algorithms are widely used for large-scale data analysis due to their low per-iteration costs, but they often suffer from slow asymptotic convergence caused by inherent variance. Variance-reduced techniques have been therefore used to address this issue in structured sparse models utilizing sparsity-inducing norms or $\ell_0$-norms. However, these techniques are not directly applicable to complex (non-convex) graph sparsity models, which are essential in applications like disease outbreak monitoring and social network analysis. In this paper, we introduce two stochastic variance-reduced gradient-based methods to solve graph sparsity optimization: GraphSVRG-IHT and GraphSCSG-IHT. We provide a general framework for theoretical analysis, demonstrating that our methods enjoy a linear convergence speed. Extensive experiments validate

Escaping Saddle Points with Stochastically Controlled Stochastic Gradient Methods

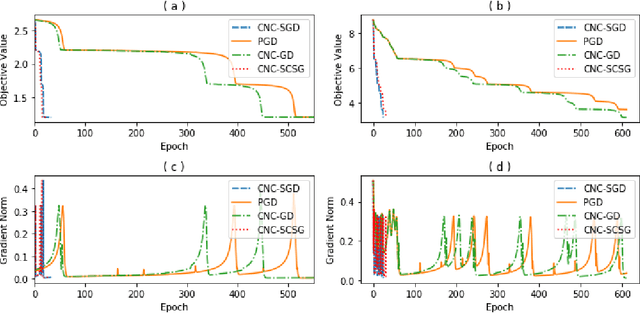
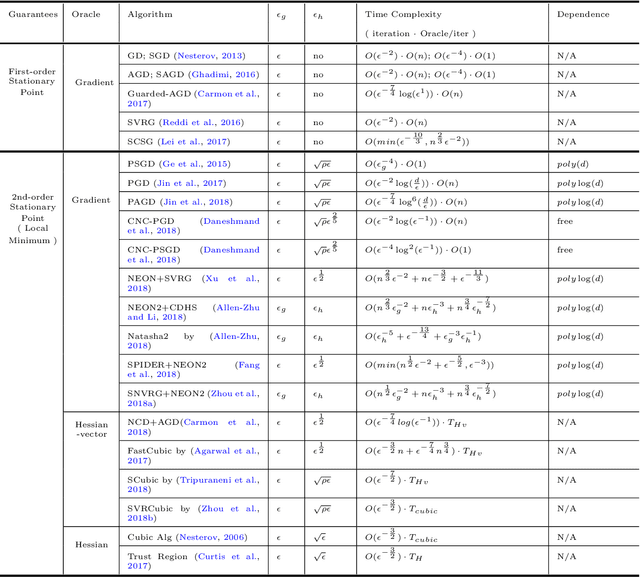
Stochastically controlled stochastic gradient (SCSG) methods have been proved to converge efficiently to first-order stationary points which, however, can be saddle points in nonconvex optimization. It has been observed that a stochastic gradient descent (SGD) step introduces anistropic noise around saddle points for deep learning and non-convex half space learning problems, which indicates that SGD satisfies the correlated negative curvature (CNC) condition for these problems. Therefore, we propose to use a separate SGD step to help the SCSG method escape from strict saddle points, resulting in the CNC-SCSG method. The SGD step plays a role similar to noise injection but is more stable. We prove that the resultant algorithm converges to a second-order stationary point with a convergence rate of $\tilde{O}( \epsilon^{-2} log( 1/\epsilon))$ where $\epsilon$ is the pre-specified error tolerance. This convergence rate is independent of the problem dimension, and is faster than that of CNC-SGD. A more general framework is further designed to incorporate the proposed CNC-SCSG into any first-order method for the method to escape saddle points. Simulation studies illustrate that the proposed algorithm can escape saddle points in much fewer epochs than the gradient descent methods perturbed by either noise injection or a SGD step.

Federated Nonconvex Sparse Learning

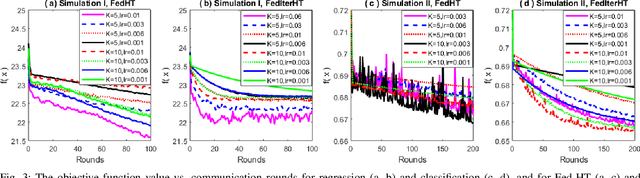
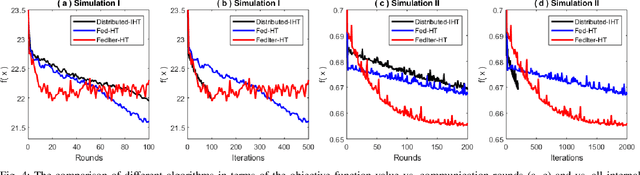
Nonconvex sparse learning plays an essential role in many areas, such as signal processing and deep network compression. Iterative hard thresholding (IHT) methods are the state-of-the-art for nonconvex sparse learning due to their capability of recovering true support and scalability with large datasets. Theoretical analysis of IHT is currently based on centralized IID data. In realistic large-scale situations, however, data are distributed, hardly IID, and private to local edge computing devices. It is thus necessary to examine the property of IHT in federated settings, which update in parallel on local devices and communicate with a central server only once in a while without sharing local data. In this paper, we propose two IHT methods: Federated Hard Thresholding (Fed-HT) and Federated Iterative Hard Thresholding (FedIter-HT). We prove that both algorithms enjoy a linear convergence rate and have strong guarantees to recover the optimal sparse estimator, similar to traditional IHT methods, but now with decentralized non-IID data. Empirical results demonstrate that the Fed-HT and FedIter-HT outperform their competitor - a distributed IHT, in terms of decreasing the objective values with lower requirements on communication rounds and bandwidth.

Effective Proximal Methods for Non-convex Non-smooth Regularized Learning

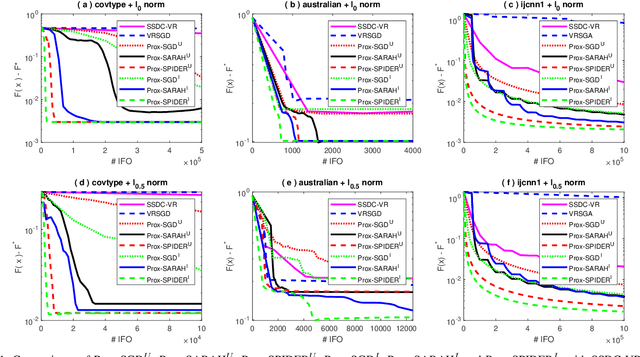
Sparse learning is a very important tool for mining useful information and patterns from high dimensional data. Non-convex non-smooth regularized learning problems play essential roles in sparse learning, and have drawn extensive attentions recently. We design a family of stochastic proximal gradient methods by applying arbitrary sampling to solve the empirical risk minimization problem with a non-convex and non-smooth regularizer. These methods draw mini-batches of training examples according to an arbitrary probability distribution when computing stochastic gradients. A unified analytic approach is developed to examine the convergence and computational complexity of these methods, allowing us to compare the different sampling schemes. We show that the independent sampling scheme tends to improve performance over the commonly-used uniform sampling scheme. Our new analysis also derives a tighter bound on convergence speed for the uniform sampling than the best one available so far. Empirical evaluations demonstrate that the proposed algorithms converge faster than the state of the art.

Effective Federated Adaptive Gradient Methods with Non-IID Decentralized Data

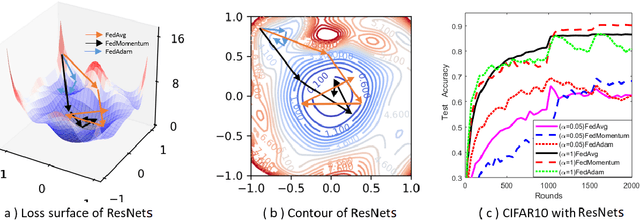
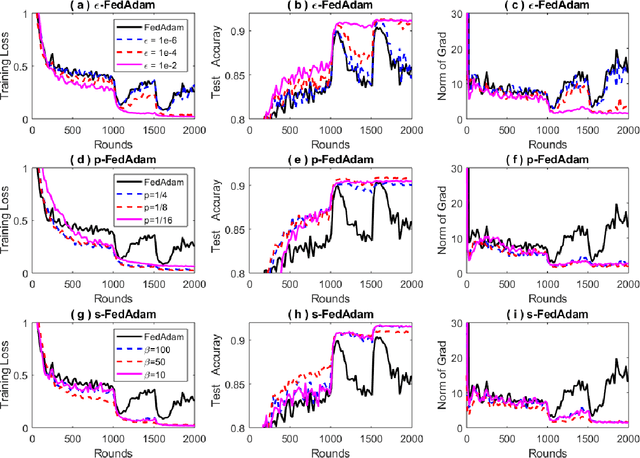
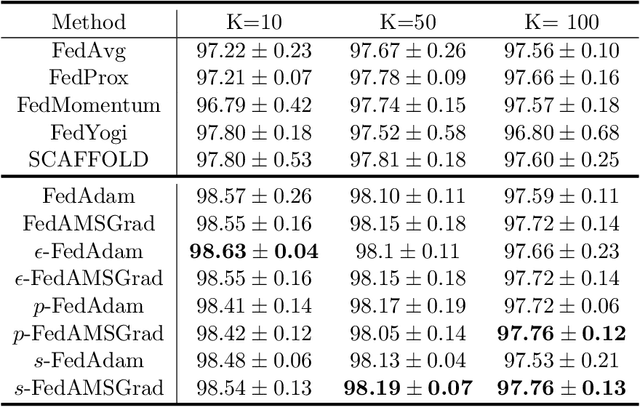
Federated learning allows loads of edge computing devices to collaboratively learn a global model without data sharing. The analysis with partial device participation under non-IID and unbalanced data reflects more reality. In this work, we propose federated learning versions of adaptive gradient methods - Federated AGMs - which employ both the first-order and second-order momenta, to alleviate generalization performance deterioration caused by dissimilarity of data population among devices. To further improve the test performance, we compare several schemes of calibration for the adaptive learning rate, including the standard Adam calibrated by $\epsilon$, $p$-Adam, and one calibrated by an activation function. Our analysis provides the first set of theoretical results that the proposed (calibrated) Federated AGMs converge to a first-order stationary point under non-IID and unbalanced data settings for nonconvex optimization. We perform extensive experiments to compare these federated learning methods with the state-of-the-art FedAvg, FedMomentum and SCAFFOLD and to assess the different calibration schemes and the advantages of AGMs over the current federated learning methods.

A Global Benchmark of Algorithms for Segmenting Late Gadolinium-Enhanced Cardiac Magnetic Resonance Imaging

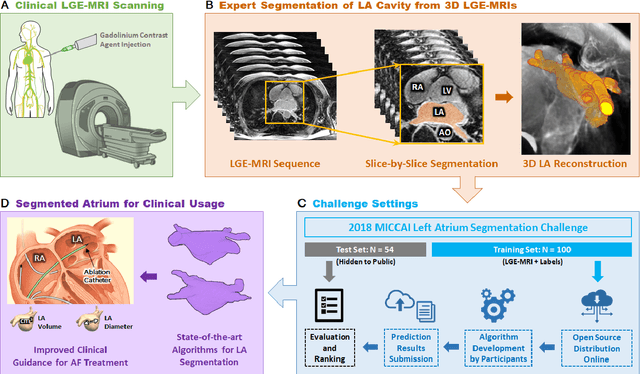
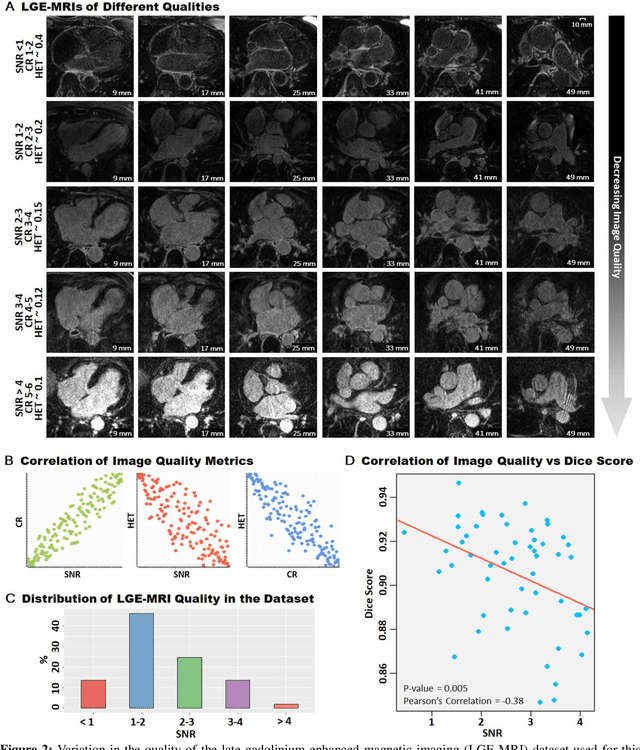
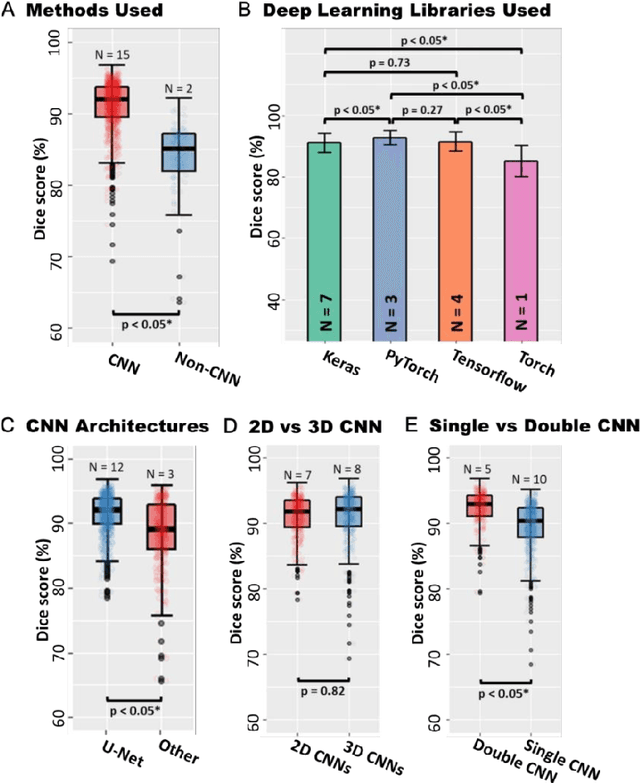
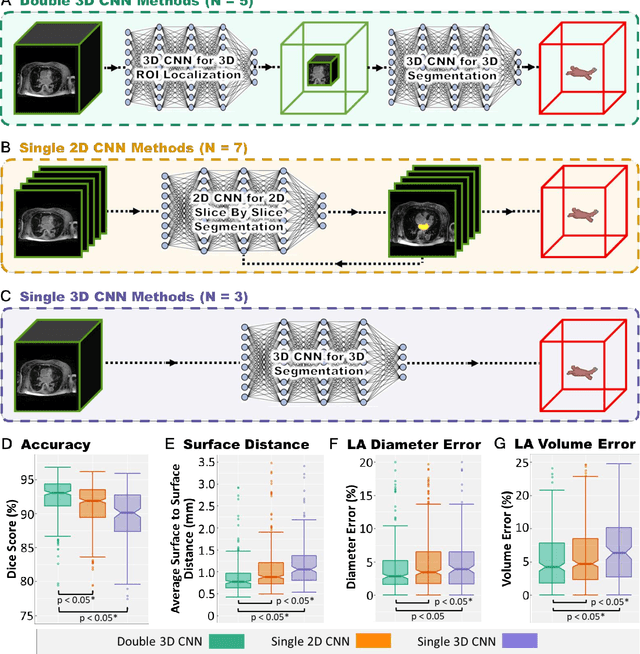
Segmentation of cardiac images, particularly late gadolinium-enhanced magnetic resonance imaging (LGE-MRI) widely used for visualizing diseased cardiac structures, is a crucial first step for clinical diagnosis and treatment. However, direct segmentation of LGE-MRIs is challenging due to its attenuated contrast. Since most clinical studies have relied on manual and labor-intensive approaches, automatic methods are of high interest, particularly optimized machine learning approaches. To address this, we organized the "2018 Left Atrium Segmentation Challenge" using 154 3D LGE-MRIs, currently the world's largest cardiac LGE-MRI dataset, and associated labels of the left atrium segmented by three medical experts, ultimately attracting the participation of 27 international teams. In this paper, extensive analysis of the submitted algorithms using technical and biological metrics was performed by undergoing subgroup analysis and conducting hyper-parameter analysis, offering an overall picture of the major design choices of convolutional neural networks (CNNs) and practical considerations for achieving state-of-the-art left atrium segmentation. Results show the top method achieved a dice score of 93.2% and a mean surface to a surface distance of 0.7 mm, significantly outperforming prior state-of-the-art. Particularly, our analysis demonstrated that double, sequentially used CNNs, in which a first CNN is used for automatic region-of-interest localization and a subsequent CNN is used for refined regional segmentation, achieved far superior results than traditional methods and pipelines containing single CNNs. This large-scale benchmarking study makes a significant step towards much-improved segmentation methods for cardiac LGE-MRIs, and will serve as an important benchmark for evaluating and comparing the future works in the field.

Calibrating the Adaptive Learning Rate to Improve Convergence of ADAM

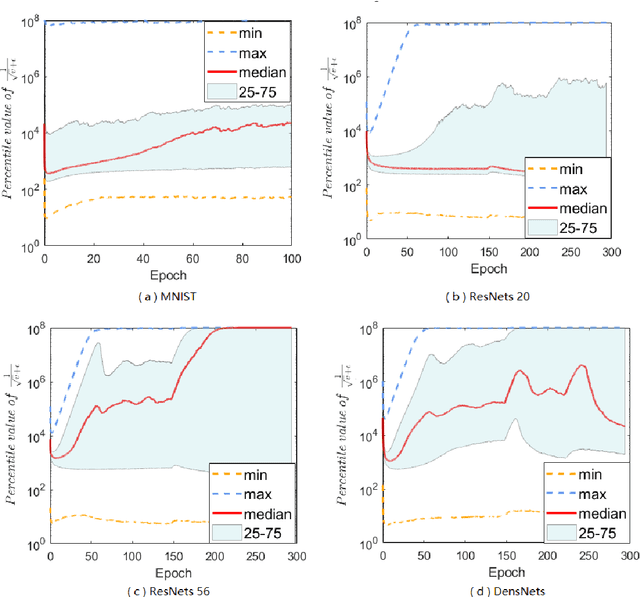
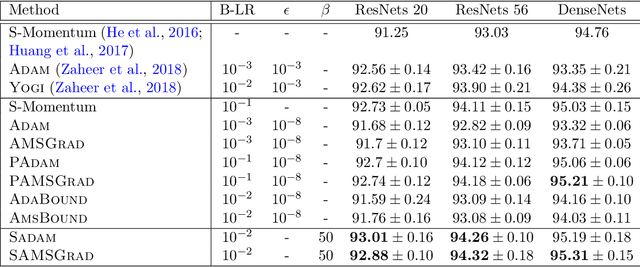
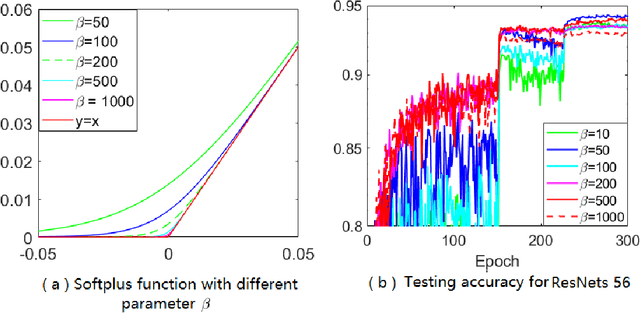
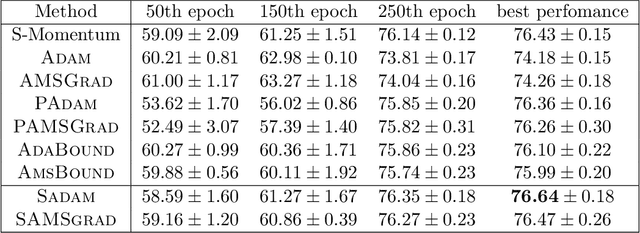
Adaptive gradient methods (AGMs) have become popular in optimizing the nonconvex problems in deep learning area. We revisit AGMs and identify that the adaptive learning rate (A-LR) used by AGMs varies significantly across the dimensions of the problem over epochs (i.e., anisotropic scale), which may lead to issues in convergence and generalization. All existing modified AGMs actually represent efforts in revising the A-LR. Theoretically, we provide a new way to analyze the convergence of AGMs and prove that the convergence rate of \textsc{Adam} also depends on its hyper-parameter $\epsilon$, which has been overlooked previously. Based on these two facts, we propose a new AGM by calibrating the A-LR with an activation ({\em softplus}) function, resulting in the \textsc{Sadam} and \textsc{SAMSGrad} methods \footnote{Code is available at https://github.com/neilliang90/Sadam.git.}. We further prove that these algorithms enjoy better convergence speed under nonconvex, non-strongly convex, and Polyak-{\L}ojasiewicz conditions compared with \textsc{Adam}. Empirical studies support our observation of the anisotropic A-LR and show that the proposed methods outperform existing AGMs and generalize even better than S-Momentum in multiple deep learning tasks.

Evaluation of Algorithms for Multi-Modality Whole Heart Segmentation: An Open-Access Grand Challenge

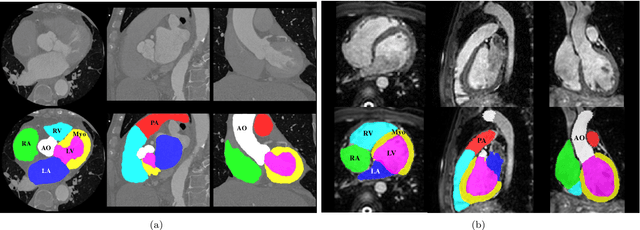
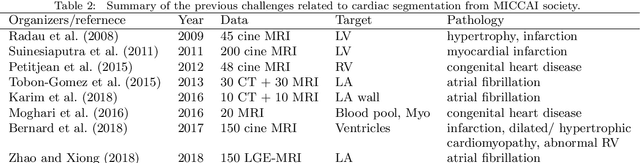
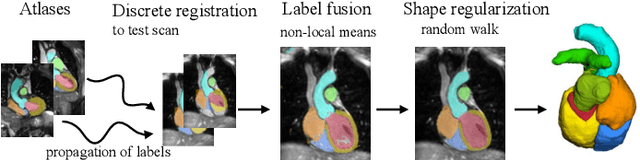
Knowledge of whole heart anatomy is a prerequisite for many clinical applications. Whole heart segmentation (WHS), which delineates substructures of the heart, can be very valuable for modeling and analysis of the anatomy and functions of the heart. However, automating this segmentation can be arduous due to the large variation of the heart shape, and different image qualities of the clinical data. To achieve this goal, a set of training data is generally needed for constructing priors or for training. In addition, it is difficult to perform comparisons between different methods, largely due to differences in the datasets and evaluation metrics used. This manuscript presents the methodologies and evaluation results for the WHS algorithms selected from the submissions to the Multi-Modality Whole Heart Segmentation (MM-WHS) challenge, in conjunction with MICCAI 2017. The challenge provides 120 three-dimensional cardiac images covering the whole heart, including 60 CT and 60 MRI volumes, all acquired in clinical environments with manual delineation. Ten algorithms for CT data and eleven algorithms for MRI data, submitted from twelve groups, have been evaluated. The results show that many of the deep learning (DL) based methods achieved high accuracy, even though the number of training datasets was limited. A number of them also reported poor results in the blinded evaluation, probably due to overfitting in their training. The conventional algorithms, mainly based on multi-atlas segmentation, demonstrated robust and stable performance, even though the accuracy is not as good as the best DL method in CT segmentation. The challenge, including the provision of the annotated training data and the blinded evaluation for submitted algorithms on the test data, continues as an ongoing benchmarking resource via its homepage (\url{www.sdspeople.fudan.edu.cn/zhuangxiahai/0/mmwhs/}).