Effective Proximal Methods for Non-convex Non-smooth Regularized Learning
Paper and Code
Oct 01, 2020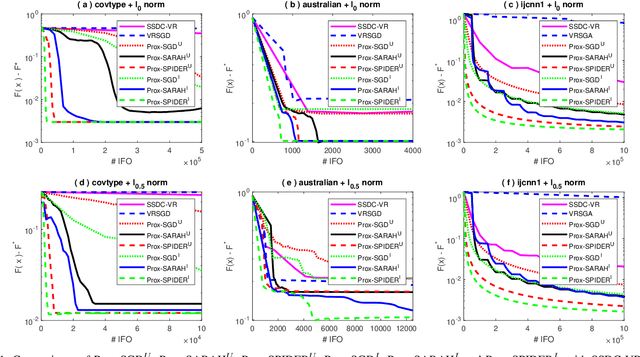
Sparse learning is a very important tool for mining useful information and patterns from high dimensional data. Non-convex non-smooth regularized learning problems play essential roles in sparse learning, and have drawn extensive attentions recently. We design a family of stochastic proximal gradient methods by applying arbitrary sampling to solve the empirical risk minimization problem with a non-convex and non-smooth regularizer. These methods draw mini-batches of training examples according to an arbitrary probability distribution when computing stochastic gradients. A unified analytic approach is developed to examine the convergence and computational complexity of these methods, allowing us to compare the different sampling schemes. We show that the independent sampling scheme tends to improve performance over the commonly-used uniform sampling scheme. Our new analysis also derives a tighter bound on convergence speed for the uniform sampling than the best one available so far. Empirical evaluations demonstrate that the proposed algorithms converge faster than the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge