Meta-Shop: Improving Item Advertisement For Small Businesses

In this paper, we study item advertisements for small businesses. This application recommends prospective customers to specific items requested by businesses. From analysis, we found that the existing Recommender Systems (RS) were ineffective for small/new businesses with a few sales history. Training samples in RS can be highly biased toward popular businesses with sufficient sales and can decrease advertising performance for small businesses. We propose a meta-learning-based RS to improve advertising performance for small/new businesses and shops: Meta-Shop. Meta-Shop leverages an advanced meta-learning optimization framework and builds a model for a shop-level recommendation. It also integrates and transfers knowledge between large and small shops, consequently learning better features in small shops. We conducted experiments on a real-world E-commerce dataset and a public benchmark dataset. Meta-Shop outperformed a production baseline and the state-of-the-art RS models. Specifically, it achieved up to 16.6% relative improvement of Recall@1M and 40.4% relative improvement of nDCG@3 for user recommendations to new shops compared to the other RS models.

An Efficient Algorithm for Deep Stochastic Contextual Bandits

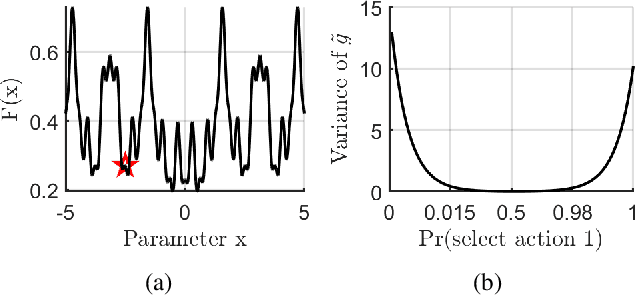
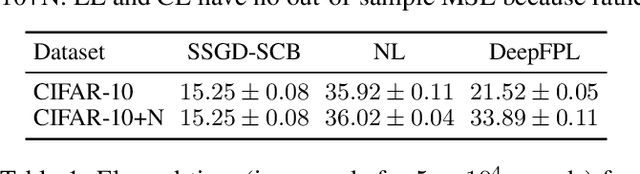
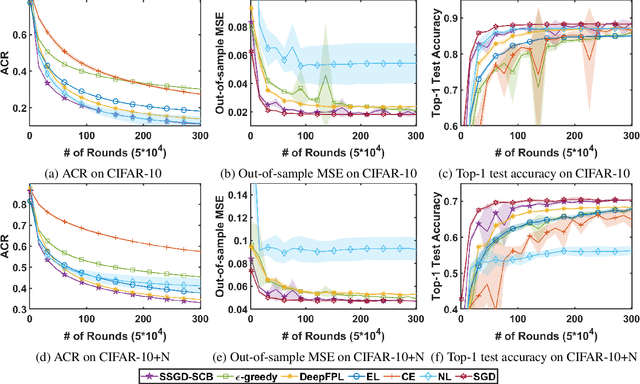
In stochastic contextual bandit (SCB) problems, an agent selects an action based on certain observed context to maximize the cumulative reward over iterations. Recently there have been a few studies using a deep neural network (DNN) to predict the expected reward for an action, and the DNN is trained by a stochastic gradient based method. However, convergence analysis has been greatly ignored to examine whether and where these methods converge. In this work, we formulate the SCB that uses a DNN reward function as a non-convex stochastic optimization problem, and design a stage-wise stochastic gradient descent algorithm to optimize the problem and determine the action policy. We prove that with high probability, the action sequence chosen by this algorithm converges to a greedy action policy respecting a local optimal reward function. Extensive experiments have been performed to demonstrate the effectiveness and efficiency of the proposed algorithm on multiple real-world datasets.

Escaping Saddle Points with Stochastically Controlled Stochastic Gradient Methods

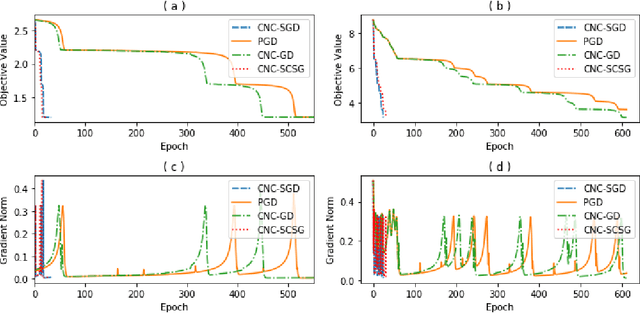
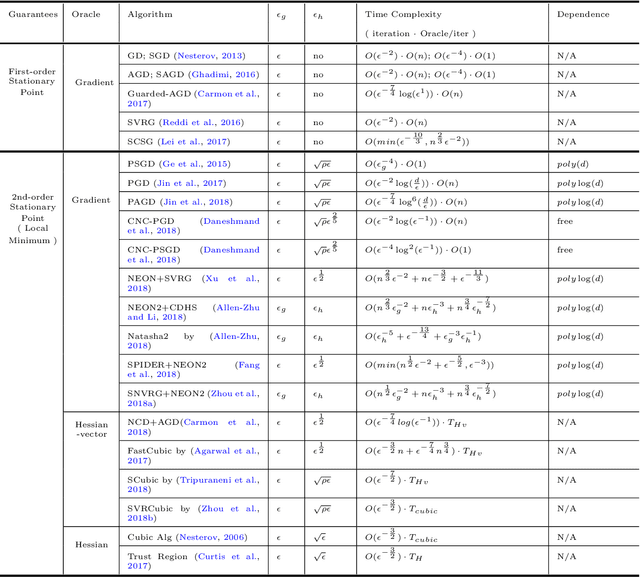
Stochastically controlled stochastic gradient (SCSG) methods have been proved to converge efficiently to first-order stationary points which, however, can be saddle points in nonconvex optimization. It has been observed that a stochastic gradient descent (SGD) step introduces anistropic noise around saddle points for deep learning and non-convex half space learning problems, which indicates that SGD satisfies the correlated negative curvature (CNC) condition for these problems. Therefore, we propose to use a separate SGD step to help the SCSG method escape from strict saddle points, resulting in the CNC-SCSG method. The SGD step plays a role similar to noise injection but is more stable. We prove that the resultant algorithm converges to a second-order stationary point with a convergence rate of $\tilde{O}( \epsilon^{-2} log( 1/\epsilon))$ where $\epsilon$ is the pre-specified error tolerance. This convergence rate is independent of the problem dimension, and is faster than that of CNC-SGD. A more general framework is further designed to incorporate the proposed CNC-SCSG into any first-order method for the method to escape saddle points. Simulation studies illustrate that the proposed algorithm can escape saddle points in much fewer epochs than the gradient descent methods perturbed by either noise injection or a SGD step.

Federated Nonconvex Sparse Learning

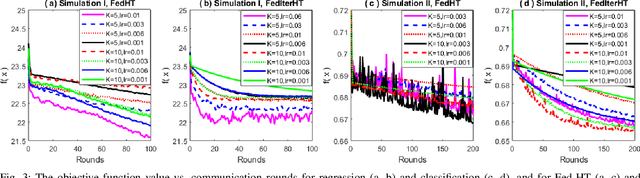
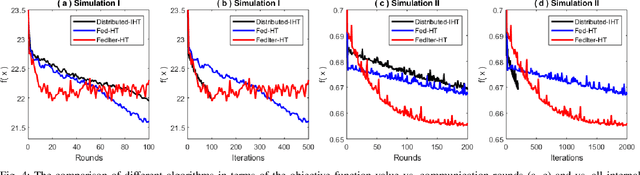
Nonconvex sparse learning plays an essential role in many areas, such as signal processing and deep network compression. Iterative hard thresholding (IHT) methods are the state-of-the-art for nonconvex sparse learning due to their capability of recovering true support and scalability with large datasets. Theoretical analysis of IHT is currently based on centralized IID data. In realistic large-scale situations, however, data are distributed, hardly IID, and private to local edge computing devices. It is thus necessary to examine the property of IHT in federated settings, which update in parallel on local devices and communicate with a central server only once in a while without sharing local data. In this paper, we propose two IHT methods: Federated Hard Thresholding (Fed-HT) and Federated Iterative Hard Thresholding (FedIter-HT). We prove that both algorithms enjoy a linear convergence rate and have strong guarantees to recover the optimal sparse estimator, similar to traditional IHT methods, but now with decentralized non-IID data. Empirical results demonstrate that the Fed-HT and FedIter-HT outperform their competitor - a distributed IHT, in terms of decreasing the objective values with lower requirements on communication rounds and bandwidth.

Effective Proximal Methods for Non-convex Non-smooth Regularized Learning

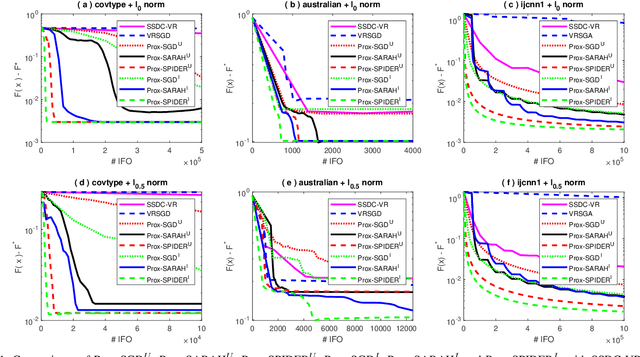
Sparse learning is a very important tool for mining useful information and patterns from high dimensional data. Non-convex non-smooth regularized learning problems play essential roles in sparse learning, and have drawn extensive attentions recently. We design a family of stochastic proximal gradient methods by applying arbitrary sampling to solve the empirical risk minimization problem with a non-convex and non-smooth regularizer. These methods draw mini-batches of training examples according to an arbitrary probability distribution when computing stochastic gradients. A unified analytic approach is developed to examine the convergence and computational complexity of these methods, allowing us to compare the different sampling schemes. We show that the independent sampling scheme tends to improve performance over the commonly-used uniform sampling scheme. Our new analysis also derives a tighter bound on convergence speed for the uniform sampling than the best one available so far. Empirical evaluations demonstrate that the proposed algorithms converge faster than the state of the art.

Effective Federated Adaptive Gradient Methods with Non-IID Decentralized Data

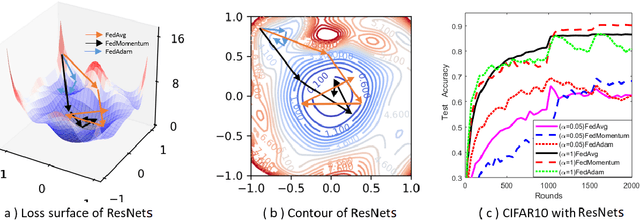
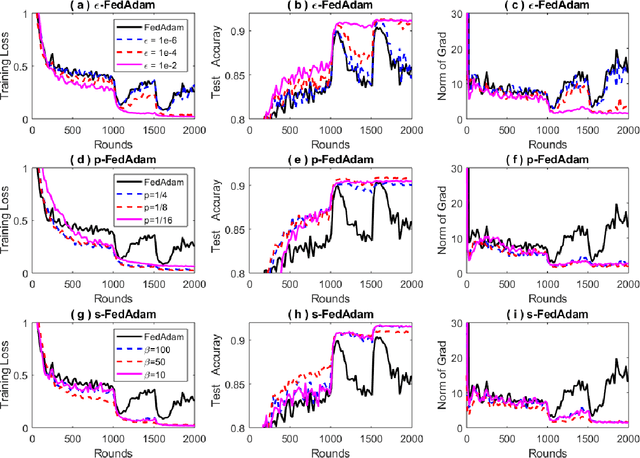
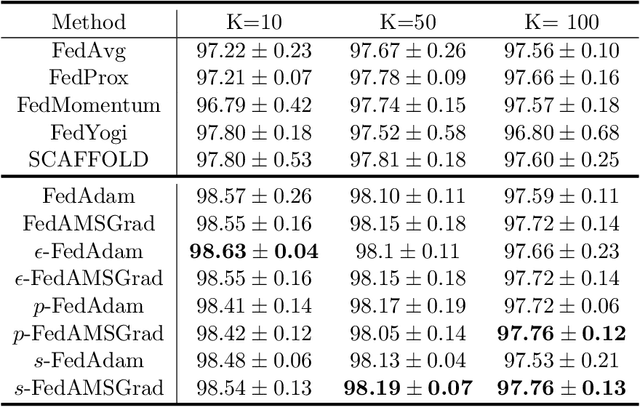
Federated learning allows loads of edge computing devices to collaboratively learn a global model without data sharing. The analysis with partial device participation under non-IID and unbalanced data reflects more reality. In this work, we propose federated learning versions of adaptive gradient methods - Federated AGMs - which employ both the first-order and second-order momenta, to alleviate generalization performance deterioration caused by dissimilarity of data population among devices. To further improve the test performance, we compare several schemes of calibration for the adaptive learning rate, including the standard Adam calibrated by $\epsilon$, $p$-Adam, and one calibrated by an activation function. Our analysis provides the first set of theoretical results that the proposed (calibrated) Federated AGMs converge to a first-order stationary point under non-IID and unbalanced data settings for nonconvex optimization. We perform extensive experiments to compare these federated learning methods with the state-of-the-art FedAvg, FedMomentum and SCAFFOLD and to assess the different calibration schemes and the advantages of AGMs over the current federated learning methods.

Towards Plausible Differentially Private ADMM Based Distributed Machine Learning

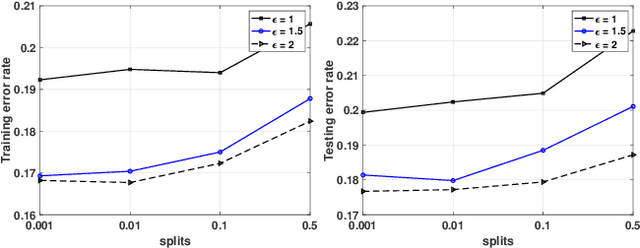
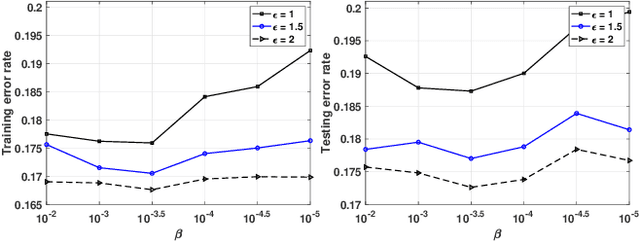
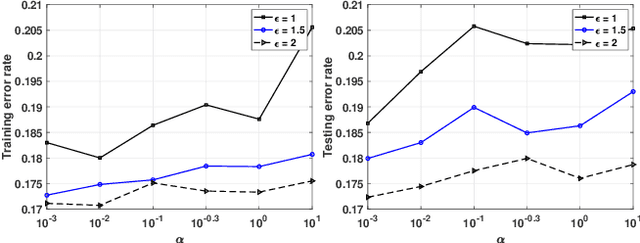
The Alternating Direction Method of Multipliers (ADMM) and its distributed version have been widely used in machine learning. In the iterations of ADMM, model updates using local private data and model exchanges among agents impose critical privacy concerns. Despite some pioneering works to relieve such concerns, differentially private ADMM still confronts many research challenges. For example, the guarantee of differential privacy (DP) relies on the premise that the optimality of each local problem can be perfectly attained in each ADMM iteration, which may never happen in practice. The model trained by DP ADMM may have low prediction accuracy. In this paper, we address these concerns by proposing a novel (Improved) Plausible differentially Private ADMM algorithm, called PP-ADMM and IPP-ADMM. In PP-ADMM, each agent approximately solves a perturbed optimization problem that is formulated from its local private data in an iteration, and then perturbs the approximate solution with Gaussian noise to provide the DP guarantee. To further improve the model accuracy and convergence, an improved version IPP-ADMM adopts sparse vector technique (SVT) to determine if an agent should update its neighbors with the current perturbed solution. The agent calculates the difference of the current solution from that in the last iteration, and if the difference is larger than a threshold, it passes the solution to neighbors; or otherwise the solution will be discarded. Moreover, we propose to track the total privacy loss under the zero-concentrated DP (zCDP) and provide a generalization performance analysis. Experiments on real-world datasets demonstrate that under the same privacy guarantee, the proposed algorithms are superior to the state of the art in terms of model accuracy and convergence rate.

Calibrating the Adaptive Learning Rate to Improve Convergence of ADAM

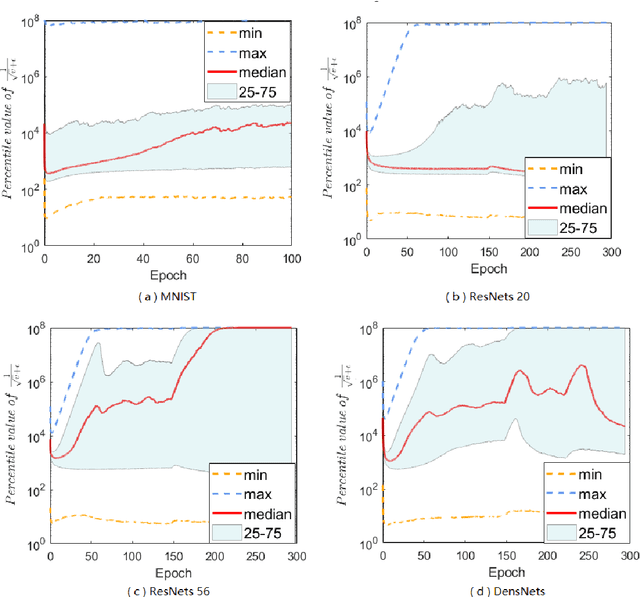
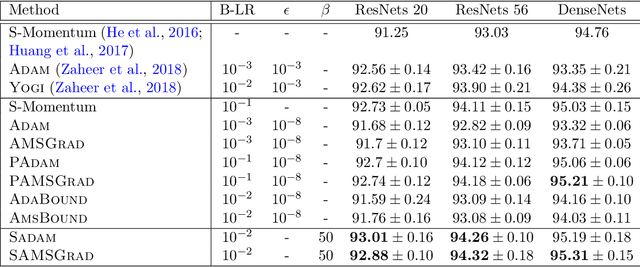
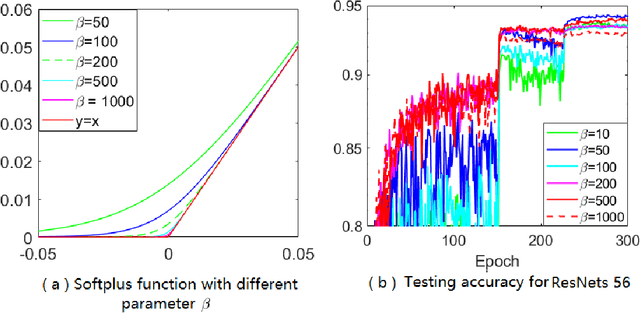
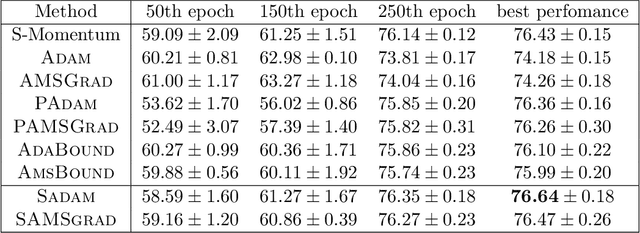
Adaptive gradient methods (AGMs) have become popular in optimizing the nonconvex problems in deep learning area. We revisit AGMs and identify that the adaptive learning rate (A-LR) used by AGMs varies significantly across the dimensions of the problem over epochs (i.e., anisotropic scale), which may lead to issues in convergence and generalization. All existing modified AGMs actually represent efforts in revising the A-LR. Theoretically, we provide a new way to analyze the convergence of AGMs and prove that the convergence rate of \textsc{Adam} also depends on its hyper-parameter $\epsilon$, which has been overlooked previously. Based on these two facts, we propose a new AGM by calibrating the A-LR with an activation ({\em softplus}) function, resulting in the \textsc{Sadam} and \textsc{SAMSGrad} methods \footnote{Code is available at https://github.com/neilliang90/Sadam.git.}. We further prove that these algorithms enjoy better convergence speed under nonconvex, non-strongly convex, and Polyak-{\L}ojasiewicz conditions compared with \textsc{Adam}. Empirical studies support our observation of the anisotropic A-LR and show that the proposed methods outperform existing AGMs and generalize even better than S-Momentum in multiple deep learning tasks.