Chunjiang Zhu
Global-Aware Enhanced Spatial-Temporal Graph Recurrent Networks: A New Framework For Traffic Flow Prediction
Jan 07, 2024



Abstract:Traffic flow prediction plays a crucial role in alleviating traffic congestion and enhancing transport efficiency. While combining graph convolution networks with recurrent neural networks for spatial-temporal modeling is a common strategy in this realm, the restricted structure of recurrent neural networks limits their ability to capture global information. For spatial modeling, many prior studies learn a graph structure that is assumed to be fixed and uniform at all time steps, which may not be true. This paper introduces a novel traffic prediction framework, Global-Aware Enhanced Spatial-Temporal Graph Recurrent Network (GA-STGRN), comprising two core components: a spatial-temporal graph recurrent neural network and a global awareness layer. Within this framework, three innovative prediction models are formulated. A sequence-aware graph neural network is proposed and integrated into the Gated Recurrent Unit (GRU) to learn non-fixed graphs at different time steps and capture local temporal relationships. To enhance the model's global perception, three distinct global spatial-temporal transformer-like architectures (GST^2) are devised for the global awareness layer. We conduct extensive experiments on four real traffic datasets and the results demonstrate the superiority of our framework and the three concrete models.
Multi-Scale Spatial-Temporal Recurrent Networks for Traffic Flow Prediction
Oct 12, 2023



Abstract:Traffic flow prediction is one of the most fundamental tasks of intelligent transportation systems. The complex and dynamic spatial-temporal dependencies make the traffic flow prediction quite challenging. Although existing spatial-temporal graph neural networks hold prominent, they often encounter challenges such as (1) ignoring the fixed graph that limits the predictive performance of the model, (2) insufficiently capturing complex spatial-temporal dependencies simultaneously, and (3) lacking attention to spatial-temporal information at different time lengths. In this paper, we propose a Multi-Scale Spatial-Temporal Recurrent Network for traffic flow prediction, namely MSSTRN, which consists of two different recurrent neural networks: the single-step gate recurrent unit and the multi-step gate recurrent unit to fully capture the complex spatial-temporal information in the traffic data under different time windows. Moreover, we propose a spatial-temporal synchronous attention mechanism that integrates adaptive position graph convolutions into the self-attention mechanism to achieve synchronous capture of spatial-temporal dependencies. We conducted extensive experiments on four real traffic datasets and demonstrated that our model achieves the best prediction accuracy with non-trivial margins compared to all the twenty baseline methods.
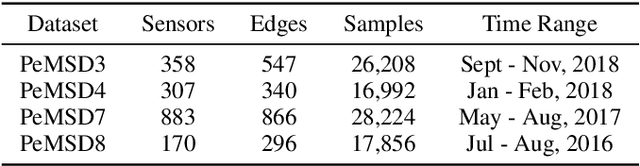
STG4Traffic: A Survey and Benchmark of Spatial-Temporal Graph Neural Networks for Traffic Prediction
Jul 02, 2023


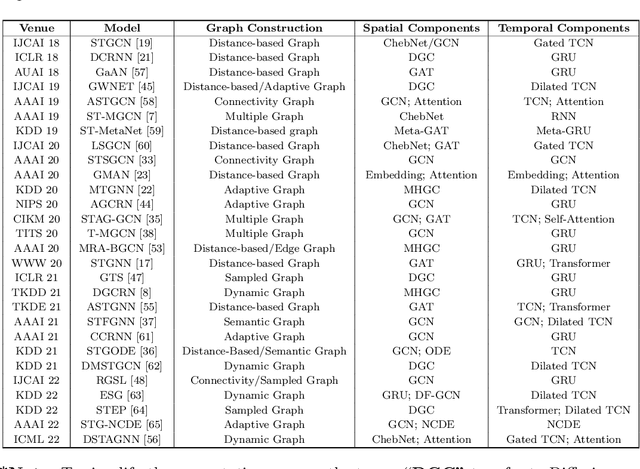
Abstract:Traffic prediction has been an active research topic in the domain of spatial-temporal data mining. Accurate real-time traffic prediction is essential to improve the safety, stability, and versatility of smart city systems, i.e., traffic control and optimal routing. The complex and highly dynamic spatial-temporal dependencies make effective predictions still face many challenges. Recent studies have shown that spatial-temporal graph neural networks exhibit great potential applied to traffic prediction, which combines sequential models with graph convolutional networks to jointly model temporal and spatial correlations. However, a survey study of graph learning, spatial-temporal graph models for traffic, as well as a fair comparison of baseline models are pending and unavoidable issues. In this paper, we first provide a systematic review of graph learning strategies and commonly used graph convolution algorithms. Then we conduct a comprehensive analysis of the strengths and weaknesses of recently proposed spatial-temporal graph network models. Furthermore, we build a study called STG4Traffic using the deep learning framework PyTorch to establish a standardized and scalable benchmark on two types of traffic datasets. We can evaluate their performance by personalizing the model settings with uniform metrics. Finally, we point out some problems in the current study and discuss future directions. Source codes are available at https://github.com/trainingl/STG4Traffic.
Attention-based Spatial-Temporal Graph Convolutional Recurrent Networks for Traffic Forecasting
Feb 25, 2023Abstract:Traffic forecasting is one of the most fundamental problems in transportation science and artificial intelligence. The key challenge is to effectively model complex spatial-temporal dependencies and correlations in modern traffic data. Existing methods, however, cannot accurately model both long-term and short-term temporal correlations simultaneously, limiting their expressive power on complex spatial-temporal patterns. In this paper, we propose a novel spatial-temporal neural network framework: Attention-based Spatial-Temporal Graph Convolutional Recurrent Network (ASTGCRN), which consists of a graph convolutional recurrent module (GCRN) and a global attention module. In particular, GCRN integrates gated recurrent units and adaptive graph convolutional networks for dynamically learning graph structures and capturing spatial dependencies and local temporal relationships. To effectively extract global temporal dependencies, we design a temporal attention layer and implement it as three independent modules based on multi-head self-attention, transformer, and informer respectively. Extensive experiments on five real traffic datasets have demonstrated the excellent predictive performance of all our three models with all their average MAE, RMSE and MAPE across the test datasets lower than the baseline methods.
Dynamic Graph Convolution Network with Spatio-Temporal Attention Fusion for Traffic Flow Prediction
Feb 24, 2023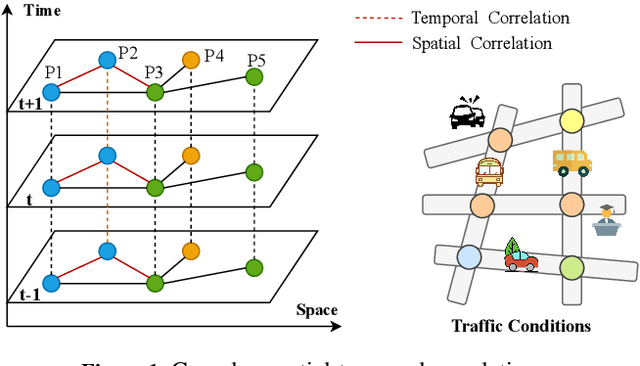
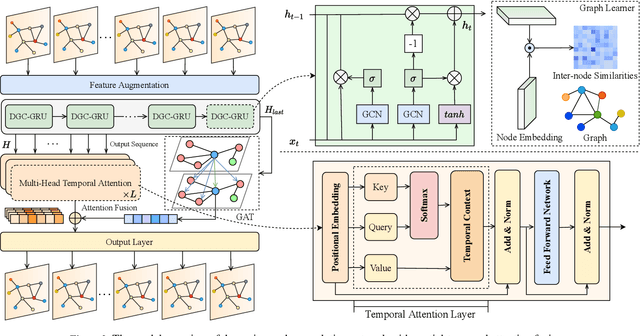
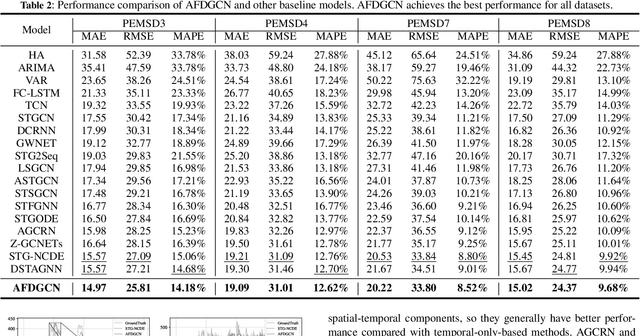
Abstract:Accurate and real-time traffic state prediction is of great practical importance for urban traffic control and web mapping services (e.g. Google Maps). With the support of massive data, deep learning methods have shown their powerful capability in capturing the complex spatio-temporal patterns of road networks. However, existing approaches use independent components to model temporal and spatial dependencies and thus ignore the heterogeneous characteristics of traffic flow that vary with time and space. In this paper, we propose a novel dynamic graph convolution network with spatio-temporal attention fusion. The method not only captures local spatio-temporal information that changes over time, but also comprehensively models long-distance and multi-scale spatio-temporal patterns based on the fusion mechanism of temporal and spatial attention. This design idea can greatly improve the spatio-temporal perception of the model. We conduct extensive experiments in 4 real-world datasets to demonstrate that our model achieves state-of-the-art performance compared to 22 baseline models.
An Efficient Algorithm for Deep Stochastic Contextual Bandits
Apr 22, 2021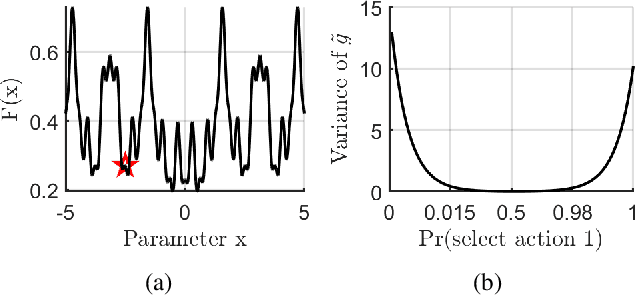
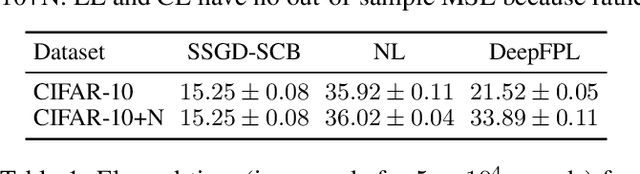

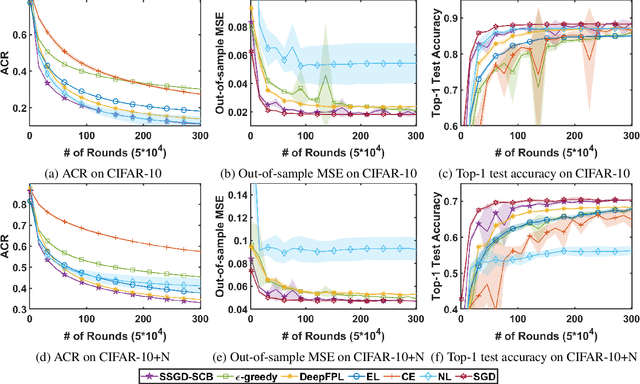
Abstract:In stochastic contextual bandit (SCB) problems, an agent selects an action based on certain observed context to maximize the cumulative reward over iterations. Recently there have been a few studies using a deep neural network (DNN) to predict the expected reward for an action, and the DNN is trained by a stochastic gradient based method. However, convergence analysis has been greatly ignored to examine whether and where these methods converge. In this work, we formulate the SCB that uses a DNN reward function as a non-convex stochastic optimization problem, and design a stage-wise stochastic gradient descent algorithm to optimize the problem and determine the action policy. We prove that with high probability, the action sequence chosen by this algorithm converges to a greedy action policy respecting a local optimal reward function. Extensive experiments have been performed to demonstrate the effectiveness and efficiency of the proposed algorithm on multiple real-world datasets.
Escaping Saddle Points with Stochastically Controlled Stochastic Gradient Methods
Mar 13, 2021
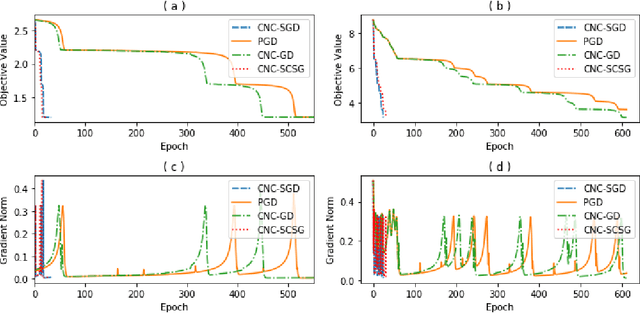
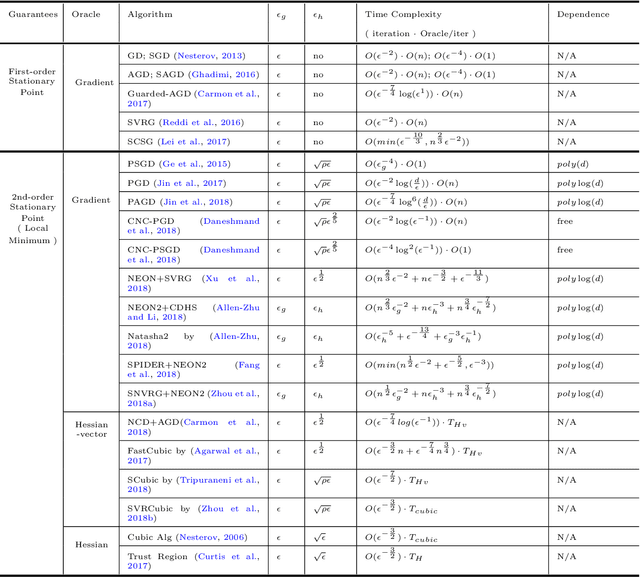
Abstract:Stochastically controlled stochastic gradient (SCSG) methods have been proved to converge efficiently to first-order stationary points which, however, can be saddle points in nonconvex optimization. It has been observed that a stochastic gradient descent (SGD) step introduces anistropic noise around saddle points for deep learning and non-convex half space learning problems, which indicates that SGD satisfies the correlated negative curvature (CNC) condition for these problems. Therefore, we propose to use a separate SGD step to help the SCSG method escape from strict saddle points, resulting in the CNC-SCSG method. The SGD step plays a role similar to noise injection but is more stable. We prove that the resultant algorithm converges to a second-order stationary point with a convergence rate of $\tilde{O}( \epsilon^{-2} log( 1/\epsilon))$ where $\epsilon$ is the pre-specified error tolerance. This convergence rate is independent of the problem dimension, and is faster than that of CNC-SGD. A more general framework is further designed to incorporate the proposed CNC-SCSG into any first-order method for the method to escape saddle points. Simulation studies illustrate that the proposed algorithm can escape saddle points in much fewer epochs than the gradient descent methods perturbed by either noise injection or a SGD step.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge