Estimation of stellar atmospheric parameters from LAMOST DR8 low-resolution spectra with 20$\leq$SNR$<$30

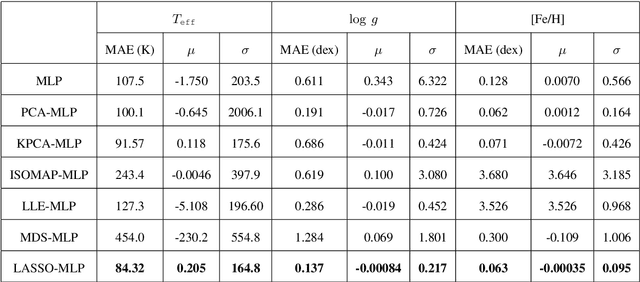
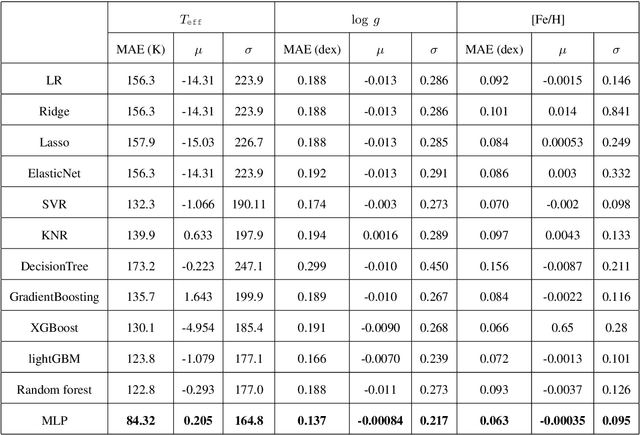
The accuracy of the estimated stellar atmospheric parameter decreases evidently with the decreasing of spectral signal-to-noise ratio (SNR) and there are a huge amount of this kind observations, especially in case of SNR$<$30. Therefore, it is helpful to improve the parameter estimation performance for these spectra and this work studied the ($T_\texttt{eff}, \log~g$, [Fe/H]) estimation problem for LAMOST DR8 low-resolution spectra with 20$\leq$SNR$<$30. We proposed a data-driven method based on machine learning techniques. Firstly, this scheme detected stellar atmospheric parameter-sensitive features from spectra by the Least Absolute Shrinkage and Selection Operator (LASSO), rejected ineffective data components and irrelevant data. Secondly, a Multi-layer Perceptron (MLP) method was used to estimate stellar atmospheric parameters from the LASSO features. Finally, the performance of the LASSO-MLP was evaluated by computing and analyzing the consistency between its estimation and the reference from the APOGEE (Apache Point Observatory Galactic Evolution Experiment) high-resolution spectra. Experiments show that the Mean Absolute Errors (MAE) of $T_\texttt{eff}, \log~g$, [Fe/H] are reduced from the LASP (137.6 K, 0.195 dex, 0.091 dex) to LASSO-MLP (84.32 K, 0.137 dex, 0.063 dex), which indicate evident improvements on stellar atmospheric parameter estimation. In addition, this work estimated the stellar atmospheric parameters for 1,162,760 low-resolution spectra with 20$\leq$SNR$<$30 from LAMOST DR8 using LASSO-MLP, and released the estimation catalog, learned model, experimental code, trained model, training data and test data for scientific exploration and algorithm study.

Trustworthy Long-Tailed Classification

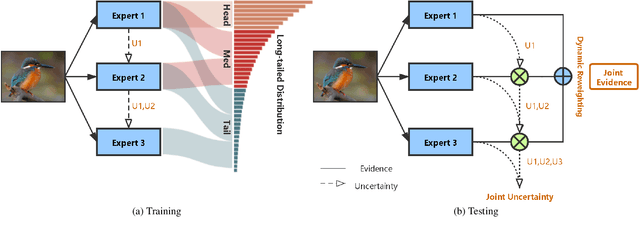
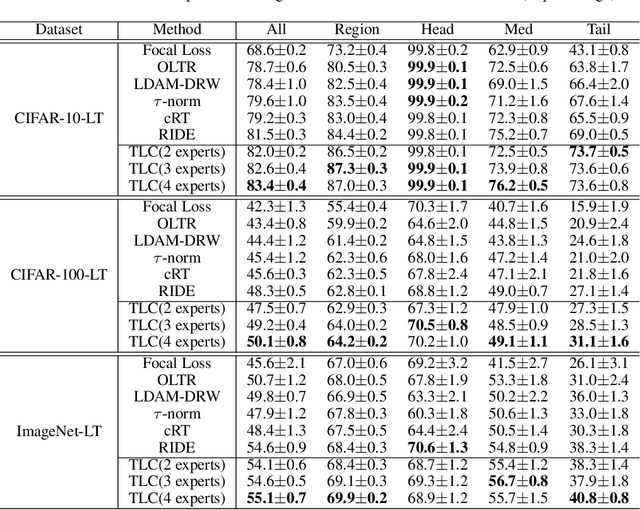
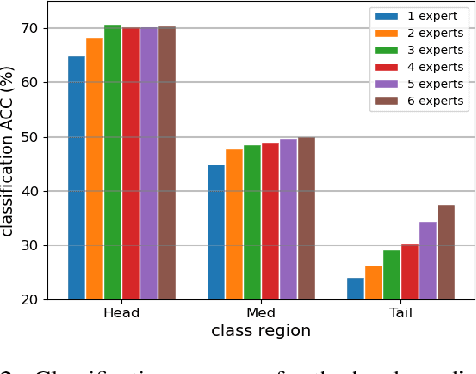
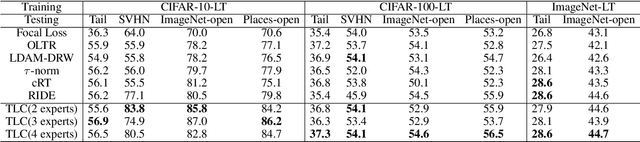
Classification on long-tailed distributed data is a challenging problem, which suffers from serious class-imbalance and accordingly unpromising performance especially on tail classes. Recently, the ensembling based methods achieve the state-of-the-art performance and show great potential. However, there are two limitations for current methods. First, their predictions are not trustworthy for failure-sensitive applications. This is especially harmful for the tail classes where the wrong predictions is basically frequent. Second, they assign unified numbers of experts to all samples, which is redundant for easy samples with excessive computational cost. To address these issues, we propose a Trustworthy Long-tailed Classification (TLC) method to jointly conduct classification and uncertainty estimation to identify hard samples in a multi-expert framework. Our TLC obtains the evidence-based uncertainty (EvU) and evidence for each expert, and then combines these uncertainties and evidences under the Dempster-Shafer Evidence Theory (DST). Moreover, we propose a dynamic expert engagement to reduce the number of engaged experts for easy samples and achieve efficiency while maintaining promising performances. Finally, we conduct comprehensive experiments on the tasks of classification, tail detection, OOD detection and failure prediction. The experimental results show that the proposed TLC outperforms the state-of-the-art methods and is trustworthy with reliable uncertainty.

An Efficient Algorithm for Deep Stochastic Contextual Bandits

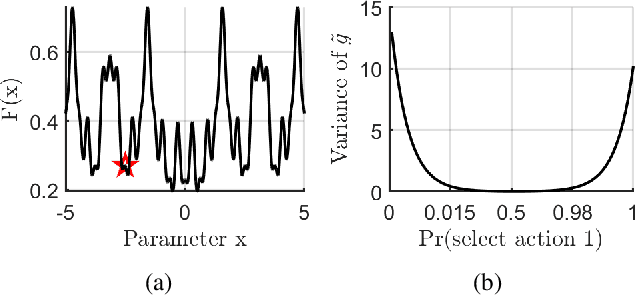
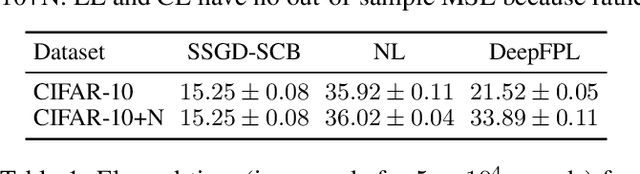
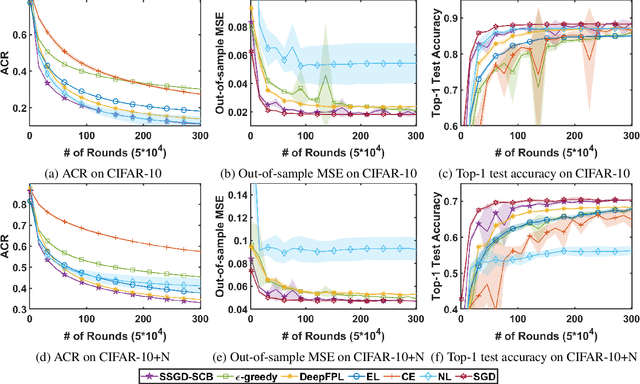
In stochastic contextual bandit (SCB) problems, an agent selects an action based on certain observed context to maximize the cumulative reward over iterations. Recently there have been a few studies using a deep neural network (DNN) to predict the expected reward for an action, and the DNN is trained by a stochastic gradient based method. However, convergence analysis has been greatly ignored to examine whether and where these methods converge. In this work, we formulate the SCB that uses a DNN reward function as a non-convex stochastic optimization problem, and design a stage-wise stochastic gradient descent algorithm to optimize the problem and determine the action policy. We prove that with high probability, the action sequence chosen by this algorithm converges to a greedy action policy respecting a local optimal reward function. Extensive experiments have been performed to demonstrate the effectiveness and efficiency of the proposed algorithm on multiple real-world datasets.