Effective Federated Adaptive Gradient Methods with Non-IID Decentralized Data
Paper and Code
Sep 14, 2020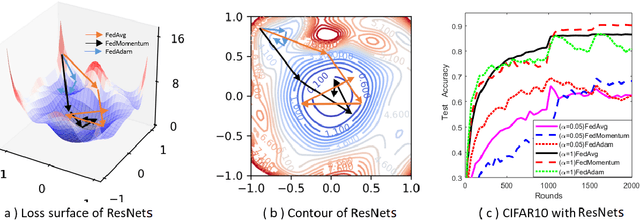

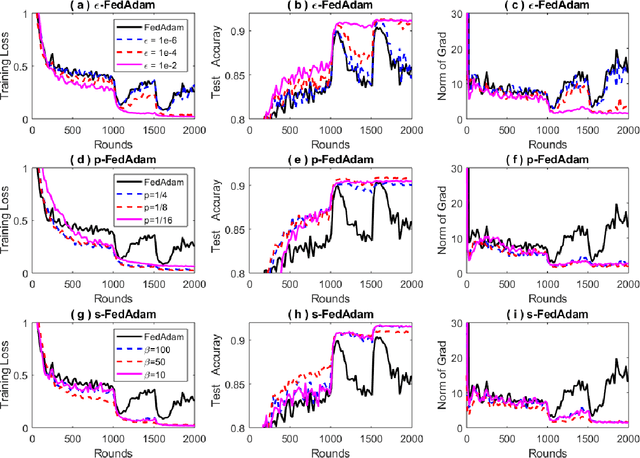
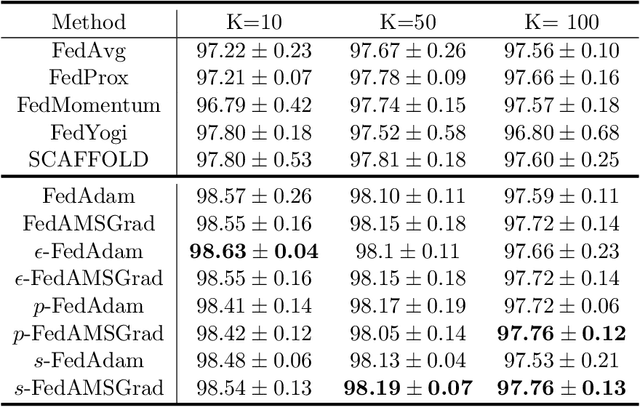
Federated learning allows loads of edge computing devices to collaboratively learn a global model without data sharing. The analysis with partial device participation under non-IID and unbalanced data reflects more reality. In this work, we propose federated learning versions of adaptive gradient methods - Federated AGMs - which employ both the first-order and second-order momenta, to alleviate generalization performance deterioration caused by dissimilarity of data population among devices. To further improve the test performance, we compare several schemes of calibration for the adaptive learning rate, including the standard Adam calibrated by $\epsilon$, $p$-Adam, and one calibrated by an activation function. Our analysis provides the first set of theoretical results that the proposed (calibrated) Federated AGMs converge to a first-order stationary point under non-IID and unbalanced data settings for nonconvex optimization. We perform extensive experiments to compare these federated learning methods with the state-of-the-art FedAvg, FedMomentum and SCAFFOLD and to assess the different calibration schemes and the advantages of AGMs over the current federated learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge