Calibrating the Adaptive Learning Rate to Improve Convergence of ADAM
Paper and Code
Sep 11, 2019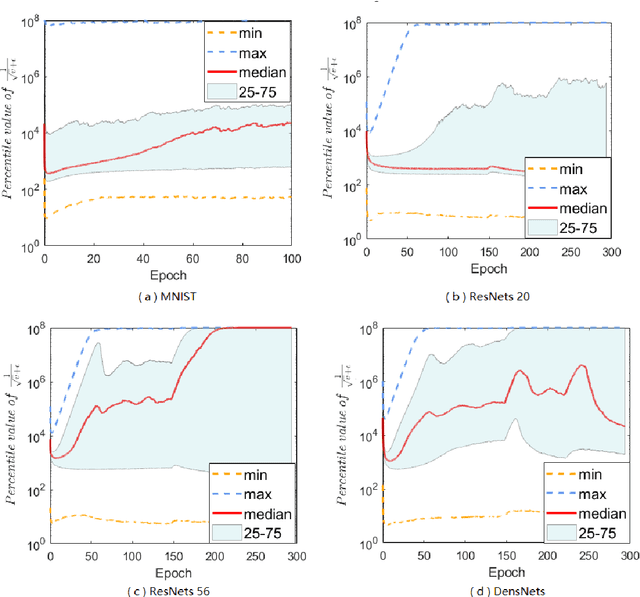
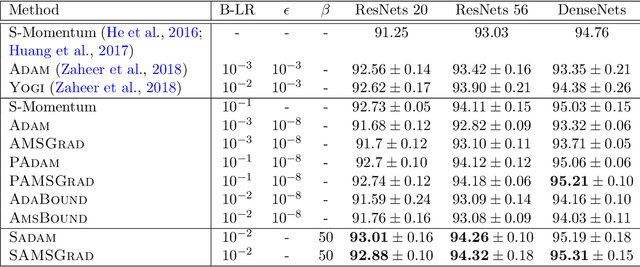
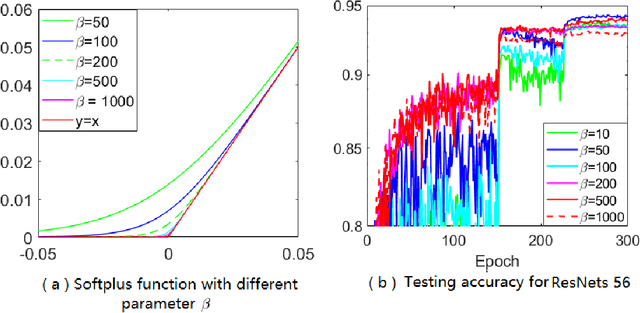
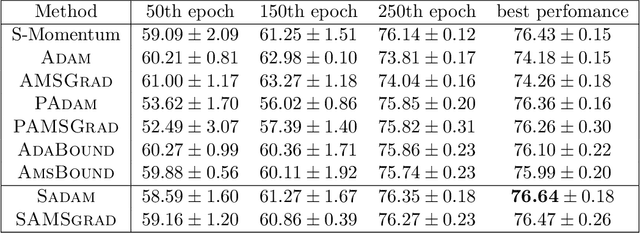
Adaptive gradient methods (AGMs) have become popular in optimizing the nonconvex problems in deep learning area. We revisit AGMs and identify that the adaptive learning rate (A-LR) used by AGMs varies significantly across the dimensions of the problem over epochs (i.e., anisotropic scale), which may lead to issues in convergence and generalization. All existing modified AGMs actually represent efforts in revising the A-LR. Theoretically, we provide a new way to analyze the convergence of AGMs and prove that the convergence rate of \textsc{Adam} also depends on its hyper-parameter $\epsilon$, which has been overlooked previously. Based on these two facts, we propose a new AGM by calibrating the A-LR with an activation ({\em softplus}) function, resulting in the \textsc{Sadam} and \textsc{SAMSGrad} methods \footnote{Code is available at https://github.com/neilliang90/Sadam.git.}. We further prove that these algorithms enjoy better convergence speed under nonconvex, non-strongly convex, and Polyak-{\L}ojasiewicz conditions compared with \textsc{Adam}. Empirical studies support our observation of the anisotropic A-LR and show that the proposed methods outperform existing AGMs and generalize even better than S-Momentum in multiple deep learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge