Optimal Differentially Private ADMM for Distributed Machine Learning

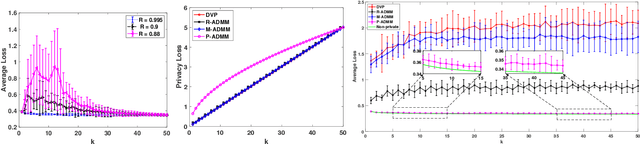
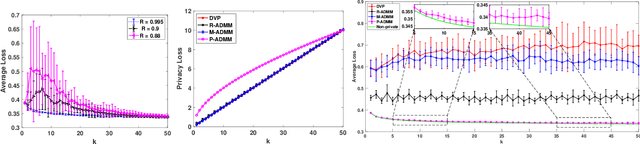
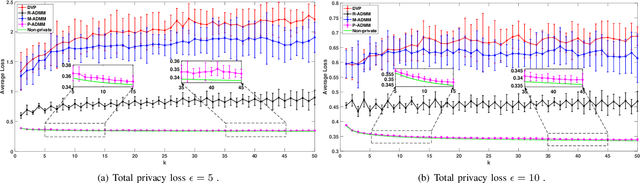
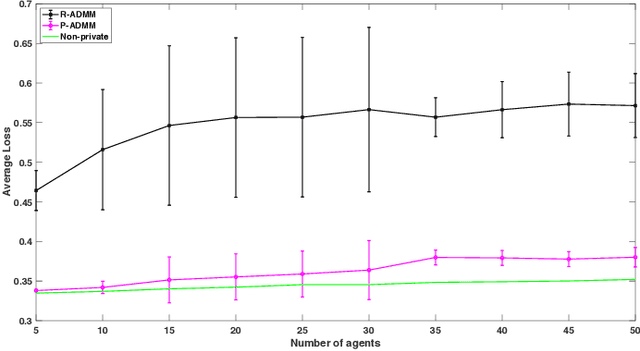
Due to massive amounts of data distributed across multiple locations, distributed machine learning has attracted a lot of research interests. Alternating Direction Method of Multipliers (ADMM) is a powerful method of designing distributed machine learning algorithm, whereby each agent computes over local datasets and exchanges computation results with its neighbor agents in an iterative procedure. There exists significant privacy leakage during this iterative process if the local data is sensitive. In this paper, we propose a differentially private ADMM algorithm (P-ADMM) to provide dynamic zero-concentrated differential privacy (dynamic zCDP), by inserting Gaussian noise with linearly decaying variance. We prove that P-ADMM has the same convergence rate compared to the non-private counterpart, i.e., $\mathcal{O}(1/K)$ with $K$ being the number of iterations and linear convergence for general convex and strongly convex problems while providing differentially private guarantee. Moreover, through our experiments performed on real-world datasets, we empirically show that P-ADMM has the best-known performance among the existing differentially private ADMM based algorithms.