AddrLLM: Address Rewriting via Large Language Model on Nationwide Logistics Data

Textual description of a physical location, commonly known as an address, plays an important role in location-based services(LBS) such as on-demand delivery and navigation. However, the prevalence of abnormal addresses, those containing inaccuracies that fail to pinpoint a location, have led to significant costs. Address rewriting has emerged as a solution to rectify these abnormal addresses. Despite the critical need, existing address rewriting methods are limited, typically tailored to correct specific error types, or frequently require retraining to process new address data effectively. In this study, we introduce AddrLLM, an innovative framework for address rewriting that is built upon a retrieval augmented large language model. AddrLLM overcomes aforementioned limitations through a meticulously designed Supervised Fine-Tuning module, an Address-centric Retrieval Augmented Generation module and a Bias-free Objective Alignment module. To the best of our knowledge, this study pioneers the application of LLM-based address rewriting approach to solve the issue of abnormal addresses. Through comprehensive offline testing with real-world data on a national scale and subsequent online deployment, AddrLLM has demonstrated superior performance in integration with existing logistics system. It has significantly decreased the rate of parcel re-routing by approximately 43\%, underscoring its exceptional efficacy in real-world applications.

MalLight: Influence-Aware Coordinated Traffic Signal Control for Traffic Signal Malfunctions

Urban traffic is subject to disruptions that cause extended waiting time and safety issues at signalized intersections. While numerous studies have addressed the issue of intelligent traffic systems in the context of various disturbances, traffic signal malfunction, a common real-world occurrence with significant repercussions, has received comparatively limited attention. The primary objective of this research is to mitigate the adverse effects of traffic signal malfunction, such as traffic congestion and collision, by optimizing the control of neighboring functioning signals. To achieve this goal, this paper presents a novel traffic signal control framework (MalLight), which leverages an Influence-aware State Aggregation Module (ISAM) and an Influence-aware Reward Aggregation Module (IRAM) to achieve coordinated control of surrounding traffic signals. To the best of our knowledge, this study pioneers the application of a Reinforcement Learning(RL)-based approach to address the challenges posed by traffic signal malfunction. Empirical investigations conducted on real-world datasets substantiate the superior performance of our proposed methodology over conventional and deep learning-based alternatives in the presence of signal malfunction, with reduction of throughput alleviated by as much as 48.6$\%$.

Differentially Private (Gradient) Expectation Maximization Algorithm with Statistical Guarantees

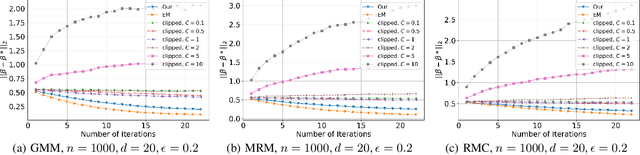
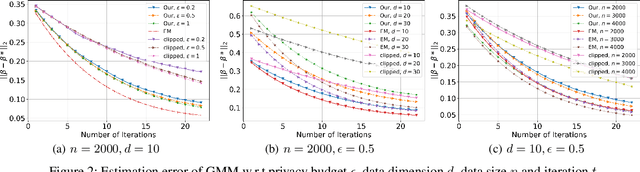
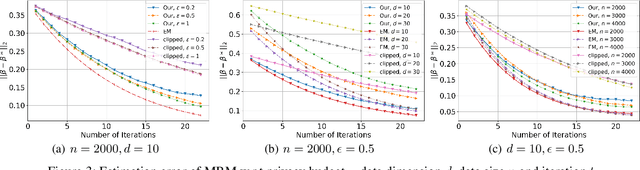
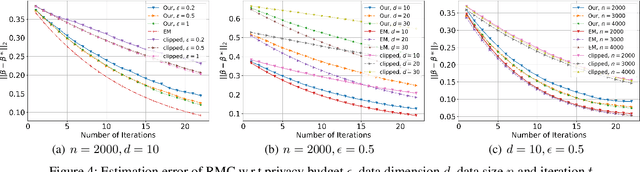
(Gradient) Expectation Maximization (EM) is a widely used algorithm for estimating the maximum likelihood of mixture models or incomplete data problems. A major challenge facing this popular technique is how to effectively preserve the privacy of sensitive data. Previous research on this problem has already lead to the discovery of some Differentially Private (DP) algorithms for (Gradient) EM. However, unlike in the non-private case, existing techniques are not yet able to provide finite sample statistical guarantees. To address this issue, we propose in this paper the first DP version of (Gradient) EM algorithm with statistical guarantees. Moreover, we apply our general framework to three canonical models: Gaussian Mixture Model (GMM), Mixture of Regressions Model (MRM) and Linear Regression with Missing Covariates (RMC). Specifically, for GMM in the DP model, our estimation error is near optimal in some cases. For the other two models, we provide the first finite sample statistical guarantees. Our theory is supported by thorough numerical experiments.