Task Assignment and Exploration Optimization for Low Altitude UAV Rescue via Generative AI Enhanced Multi-agent Reinforcement Learning

Artificial Intelligence (AI)-driven convolutional neural networks enhance rescue, inspection, and surveillance tasks performed by low-altitude uncrewed aerial vehicles (UAVs) and ground computing nodes (GCNs) in unknown environments. However, their high computational demands often exceed a single UAV's capacity, leading to system instability, further exacerbated by the limited and dynamic resources of GCNs. To address these challenges, this paper proposes a novel cooperation framework involving UAVs, ground-embedded robots (GERs), and high-altitude platforms (HAPs), which enable resource pooling through UAV-to-GER (U2G) and UAV-to-HAP (U2H) communications to provide computing services for UAV offloaded tasks. Specifically, we formulate the multi-objective optimization problem of task assignment and exploration optimization in UAVs as a dynamic long-term optimization problem. Our objective is to minimize task completion time and energy consumption while ensuring system stability over time. To achieve this, we first employ the Lyapunov optimization technique to transform the original problem, with stability constraints, into a per-slot deterministic problem. We then propose an algorithm named HG-MADDPG, which combines the Hungarian algorithm with a generative diffusion model (GDM)-based multi-agent deep deterministic policy gradient (MADDPG) approach. We first introduce the Hungarian algorithm as a method for exploration area selection, enhancing UAV efficiency in interacting with the environment. We then innovatively integrate the GDM and multi-agent deep deterministic policy gradient (MADDPG) to optimize task assignment decisions, such as task offloading and resource allocation. Simulation results demonstrate the effectiveness of the proposed approach, with significant improvements in task offloading efficiency, latency reduction, and system stability compared to baseline methods.

Satisfaction-Aware Incentive Scheme for Federated Learning in Industrial Metaverse: DRL-Based Stackbelberg Game Approach

Industrial Metaverse leverages the Industrial Internet of Things (IIoT) to integrate data from diverse devices, employing federated learning and meta-computing to train models in a distributed manner while ensuring data privacy. Achieving an immersive experience for industrial Metaverse necessitates maintaining a balance between model quality and training latency. Consequently, a primary challenge in federated learning tasks is optimizing overall system performance by balancing model quality and training latency. This paper designs a satisfaction function that accounts for data size, Age of Information (AoI), and training latency. Additionally, the satisfaction function is incorporated into the utility functions to incentivize node participation in model training. We model the utility functions of servers and nodes as a two-stage Stackelberg game and employ a deep reinforcement learning approach to learn the Stackelberg equilibrium. This approach ensures balanced rewards and enhances the applicability of the incentive scheme for industrial Metaverse. Simulation results demonstrate that, under the same budget constraints, the proposed incentive scheme improves at least 23.7% utility compared to existing schemes without compromising model accuracy.

DNN Task Assignment in UAV Networks: A Generative AI Enhanced Multi-Agent Reinforcement Learning Approach

Unmanned Aerial Vehicles (UAVs) possess high mobility and flexible deployment capabilities, prompting the development of UAVs for various application scenarios within the Internet of Things (IoT). The unique capabilities of UAVs give rise to increasingly critical and complex tasks in uncertain and potentially harsh environments. The substantial amount of data generated from these applications necessitates processing and analysis through deep neural networks (DNNs). However, UAVs encounter challenges due to their limited computing resources when managing DNN models. This paper presents a joint approach that combines multiple-agent reinforcement learning (MARL) and generative diffusion models (GDM) for assigning DNN tasks to a UAV swarm, aimed at reducing latency from task capture to result output. To address these challenges, we first consider the task size of the target area to be inspected and the shortest flying path as optimization constraints, employing a greedy algorithm to resolve the subproblem with a focus on minimizing the UAV's flying path and the overall system cost. In the second stage, we introduce a novel DNN task assignment algorithm, termed GDM-MADDPG, which utilizes the reverse denoising process of GDM to replace the actor network in multi-agent deep deterministic policy gradient (MADDPG). This approach generates specific DNN task assignment actions based on agents' observations in a dynamic environment. Simulation results indicate that our algorithm performs favorably compared to benchmarks in terms of path planning, Age of Information (AoI), energy consumption, and task load balancing.

Differentially Private and Fair Classification via Calibrated Functional Mechanism

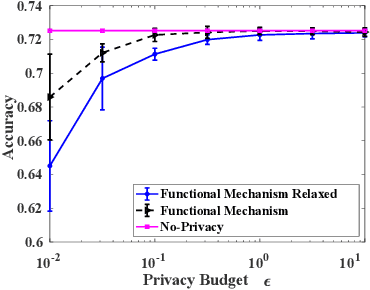
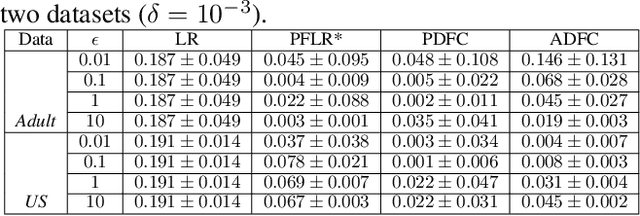
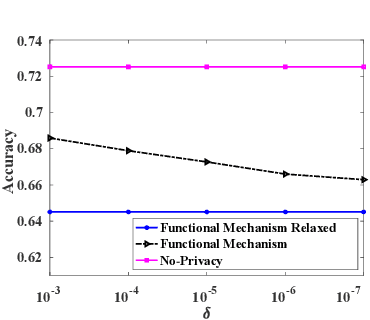
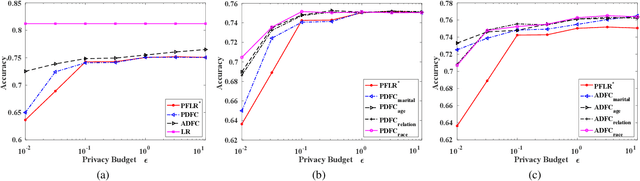
Machine learning is increasingly becoming a powerful tool to make decisions in a wide variety of applications, such as medical diagnosis and autonomous driving. Privacy concerns related to the training data and unfair behaviors of some decisions with regard to certain attributes (e.g., sex, race) are becoming more critical. Thus, constructing a fair machine learning model while simultaneously providing privacy protection becomes a challenging problem. In this paper, we focus on the design of classification model with fairness and differential privacy guarantees by jointly combining functional mechanism and decision boundary fairness. In order to enforce $\epsilon$-differential privacy and fairness, we leverage the functional mechanism to add different amounts of Laplace noise regarding different attributes to the polynomial coefficients of the objective function in consideration of fairness constraint. We further propose an utility-enhancement scheme, called relaxed functional mechanism by adding Gaussian noise instead of Laplace noise, hence achieving $(\epsilon,\delta)$-differential privacy. Based on the relaxed functional mechanism, we can design $(\epsilon,\delta)$-differentially private and fair classification model. Moreover, our theoretical analysis and empirical results demonstrate that our two approaches achieve both fairness and differential privacy while preserving good utility and outperform the state-of-the-art algorithms.