Differential Equation Units: Learning Functional Forms of Activation Functions from Data
Paper and Code
Sep 06, 2019

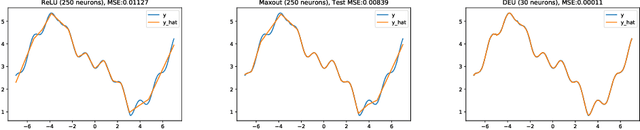
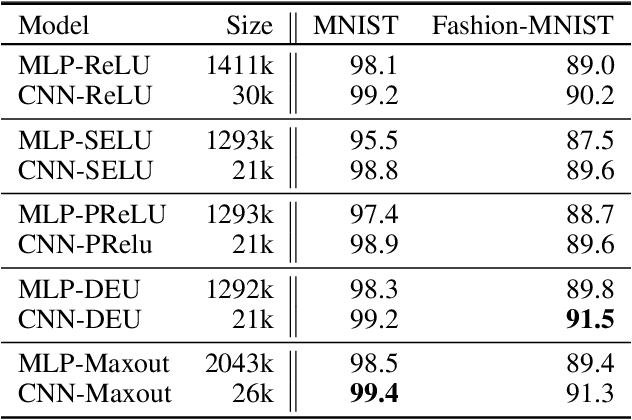
Most deep neural networks use simple, fixed activation functions, such as sigmoids or rectified linear units, regardless of domain or network structure. We introduce differential equation units (DEUs), an improvement to modern neural networks, which enables each neuron to learn a particular nonlinear activation function from a family of solutions to an ordinary differential equation. Specifically, each neuron may change its functional form during training based on the behavior of the other parts of the network. We show that using neurons with DEU activation functions results in a more compact network capable of achieving comparable, if not superior, performance when is compared to much larger networks.
* arXiv admin note: text overlap with arXiv:1905.07685
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge