Byzantine-Resilient Non-Convex Stochastic Gradient Descent
Paper and Code
Dec 28, 2020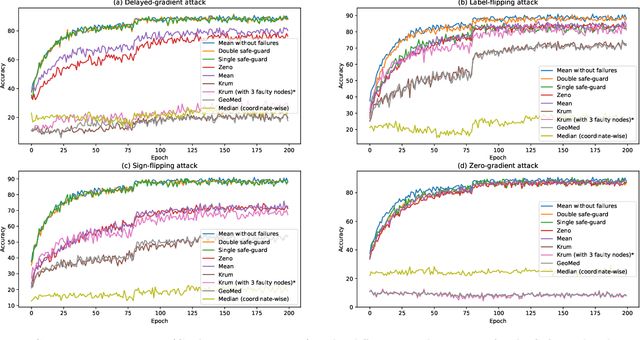
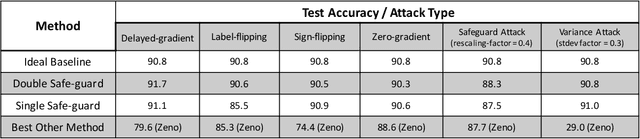
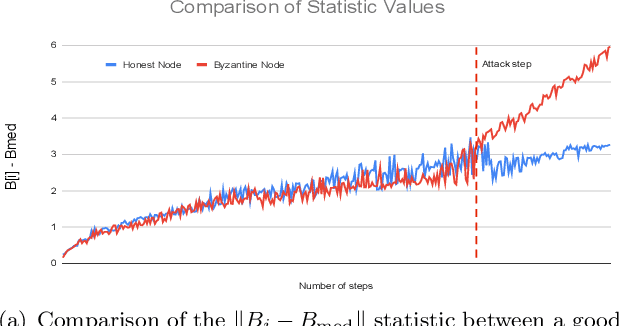
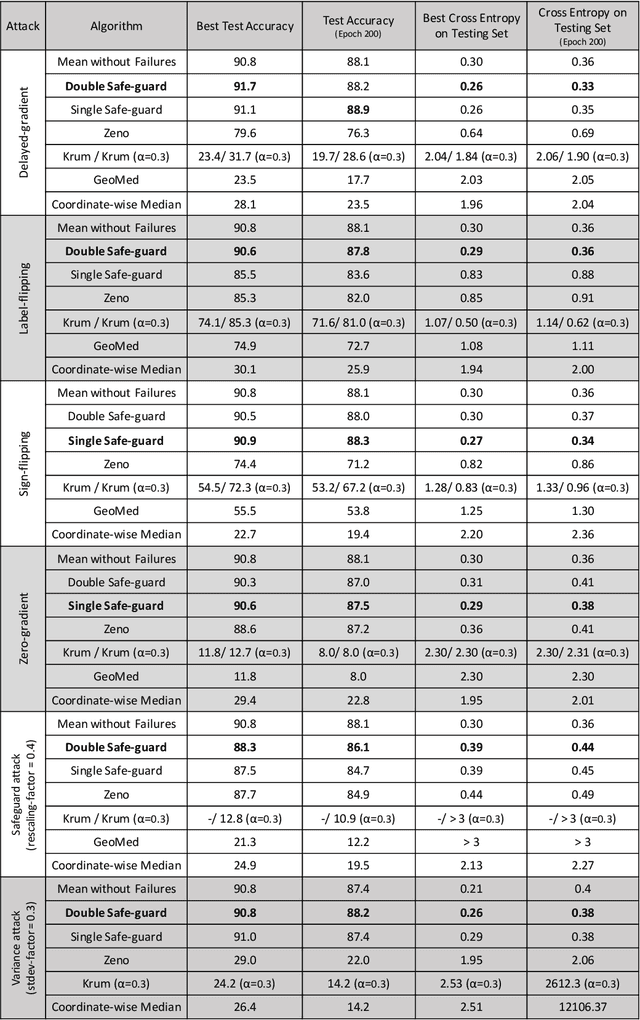
We study adversary-resilient stochastic distributed optimization, in which $m$ machines can independently compute stochastic gradients, and cooperate to jointly optimize over their local objective functions. However, an $\alpha$-fraction of the machines are $\textit{Byzantine}$, in that they may behave in arbitrary, adversarial ways. We consider a variant of this procedure in the challenging $\textit{non-convex}$ case. Our main result is a new algorithm SafeguardSGD which can provably escape saddle points and find approximate local minima of the non-convex objective. The algorithm is based on a new concentration filtering technique, and its sample and time complexity bounds match the best known theoretical bounds in the stochastic, distributed setting when no Byzantine machines are present. Our algorithm is practical: it improves upon the performance of prior methods when training deep neural networks, it is relatively lightweight, and is the first method to withstand two recently-proposed Byzantine attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge