A Study of Performance of Optimal Transport
Paper and Code
May 03, 2020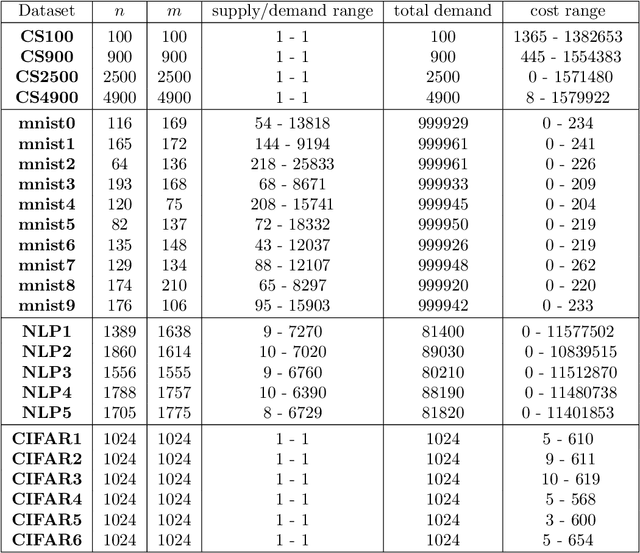
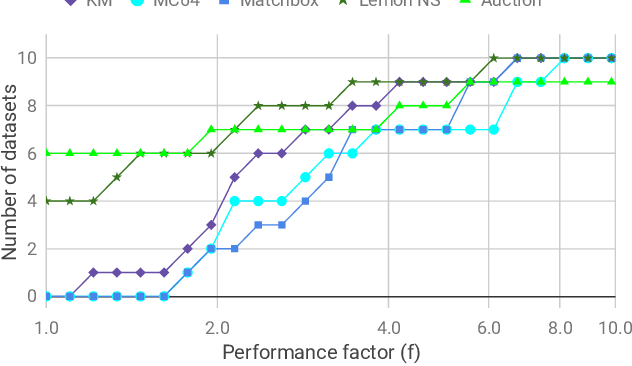
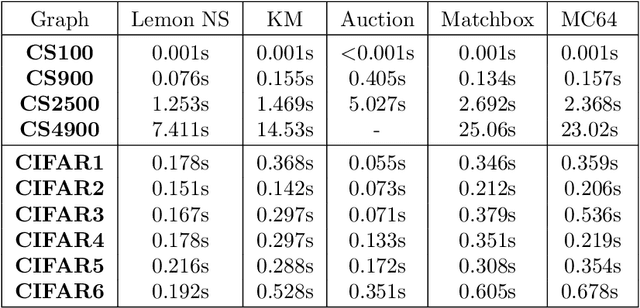
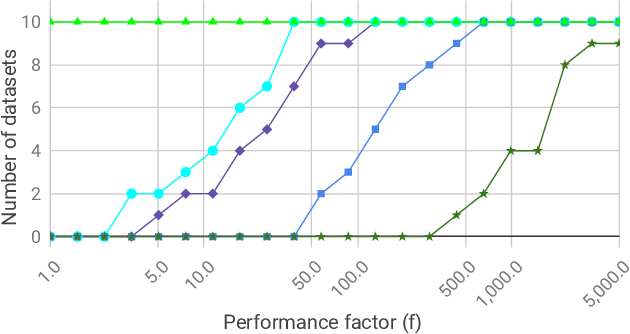
We investigate the problem of efficiently computing optimal transport (OT) distances, which is equivalent to the node-capacitated minimum cost maximum flow problem in a bipartite graph. We compare runtimes in computing OT distances on data from several domains, such as synthetic data of geometric shapes, embeddings of tokens in documents, and pixels in images. We show that in practice, combinatorial methods such as network simplex and augmenting path based algorithms can consistently outperform numerical matrix-scaling based methods such as Sinkhorn [Cuturi'13] and Greenkhorn [Altschuler et al'17], even in low accuracy regimes, with up to orders of magnitude speedups. Lastly, we present a new combinatorial algorithm that improves upon the classical Kuhn-Munkres algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge