Randomized Smoothing of All Shapes and Sizes
Paper and Code
Mar 04, 2020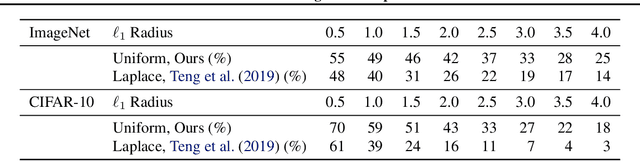

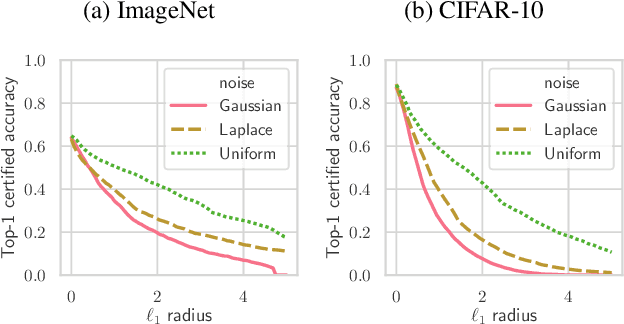
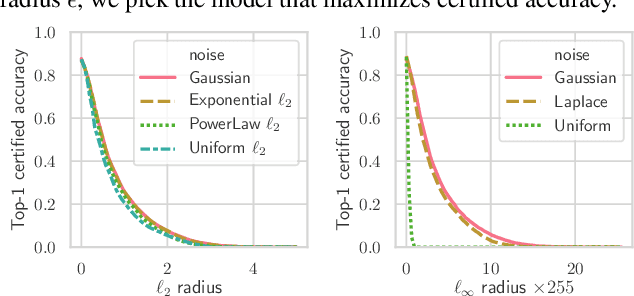
Randomized smoothing is a recently proposed defense against adversarial attacks that has achieved state-of-the-art provable robustness against $\ell_2$ perturbations. Soon after, a number of works devised new randomized smoothing schemes for other metrics, such as $\ell_1$ or $\ell_\infty$; however, for each geometry, substantial effort was needed to derive new robustness guarantees. This begs the question: can we find a general theory for randomized smoothing? In this work we propose a novel framework for devising and analyzing randomized smoothing schemes, and validate its effectiveness in practice. Our theoretical contributions are as follows: (1) We show that for an appropriate notion of "optimal", the optimal smoothing distributions for any "nice" norm have level sets given by the *Wulff Crystal* of that norm. (2) We propose two novel and complementary methods for deriving provably robust radii for any smoothing distribution. Finally, (3) we show fundamental limits to current randomized smoothing techniques via the theory of *Banach space cotypes*. By combining (1) and (2), we significantly improve the state-of-the-art certified accuracy in $\ell_1$ on standard datasets. On the other hand, using (3), we show that, without more information than label statistics under random input perturbations, randomized smoothing cannot achieve nontrivial certified accuracy against perturbations of $\ell_p$-norm $\Omega(\min(1, d^{\frac{1}{p}-\frac{1}{2}}))$, when the input dimension $d$ is large. We provide code in github.com/tonyduan/rs4a.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge