A Polynomial-Time Approximation for Pairwise Fair $k$-Median Clustering

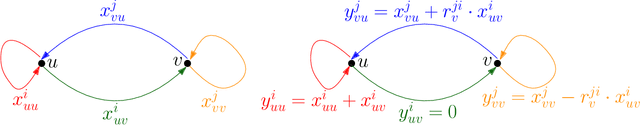
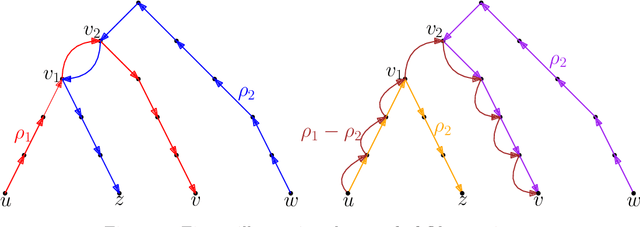
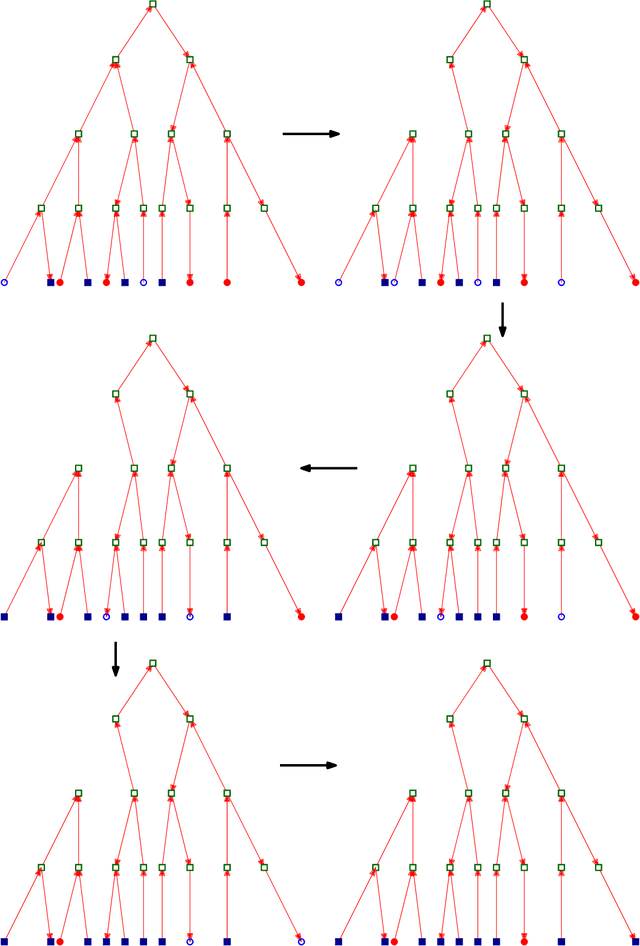
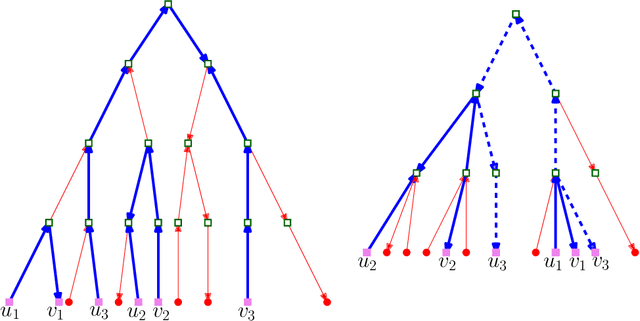
In this work, we study pairwise fair clustering with $\ell \ge 2$ groups, where for every cluster $C$ and every group $i \in [\ell]$, the number of points in $C$ from group $i$ must be at most $t$ times the number of points in $C$ from any other group $j \in [\ell]$, for a given integer $t$. To the best of our knowledge, only bi-criteria approximation and exponential-time algorithms follow for this problem from the prior work on fair clustering problems when $\ell > 2$. In our work, focusing on the $\ell > 2$ case, we design the first polynomial-time $(t^{\ell}\cdot \ell\cdot k)^{O(\ell)}$-approximation for this problem with $k$-median cost that does not violate the fairness constraints. We complement our algorithmic result by providing hardness of approximation results, which show that our problem even when $\ell=2$ is almost as hard as the popular uniform capacitated $k$-median, for which no polynomial-time algorithm with an approximation factor of $o(\log k)$ is known.

Fair Representation Clustering with Several Protected Classes

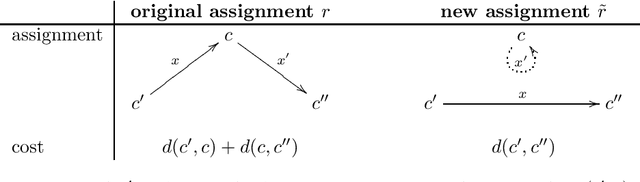
We study the problem of fair $k$-median where each cluster is required to have a fair representation of individuals from different groups. In the fair representation $k$-median problem, we are given a set of points $X$ in a metric space. Each point $x\in X$ belongs to one of $\ell$ groups. Further, we are given fair representation parameters $\alpha_j$ and $\beta_j$ for each group $j\in [\ell]$. We say that a $k$-clustering $C_1, \cdots, C_k$ fairly represents all groups if the number of points from group $j$ in cluster $C_i$ is between $\alpha_j |C_i|$ and $\beta_j |C_i|$ for every $j\in[\ell]$ and $i\in [k]$. The goal is to find a set $\mathcal{C}$ of $k$ centers and an assignment $\phi: X\rightarrow \mathcal{C}$ such that the clustering defined by $(\mathcal{C}, \phi)$ fairly represents all groups and minimizes the $\ell_1$-objective $\sum_{x\in X} d(x, \phi(x))$. We present an $O(\log k)$-approximation algorithm that runs in time $n^{O(\ell)}$. Note that the known algorithms for the problem either (i) violate the fairness constraints by an additive term or (ii) run in time that is exponential in both $k$ and $\ell$. We also consider an important special case of the problem where $\alpha_j = \beta_j = \frac{f_j}{f}$ and $f_j, f \in \mathbb{N}$ for all $j\in [\ell]$. For this special case, we present an $O(\log k)$-approximation algorithm that runs in $(kf)^{O(\ell)}\log n + poly(n)$ time.

Approximating Fair Clustering with Cascaded Norm Objectives

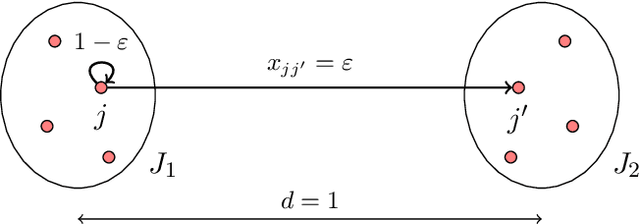
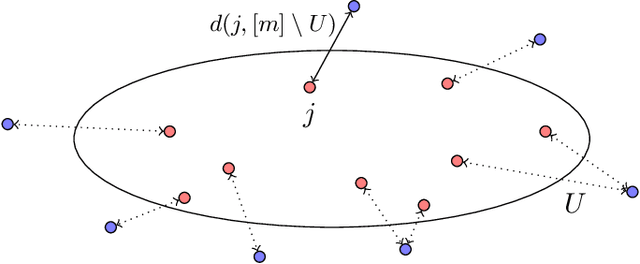
We introduce the $(p,q)$-Fair Clustering problem. In this problem, we are given a set of points $P$ and a collection of different weight functions $W$. We would like to find a clustering which minimizes the $\ell_q$-norm of the vector over $W$ of the $\ell_p$-norms of the weighted distances of points in $P$ from the centers. This generalizes various clustering problems, including Socially Fair $k$-Median and $k$-Means, and is closely connected to other problems such as Densest $k$-Subgraph and Min $k$-Union. We utilize convex programming techniques to approximate the $(p,q)$-Fair Clustering problem for different values of $p$ and $q$. When $p\geq q$, we get an $O(k^{(p-q)/(2pq)})$, which nearly matches a $k^{\Omega((p-q)/(pq))}$ lower bound based on conjectured hardness of Min $k$-Union and other problems. When $q\geq p$, we get an approximation which is independent of the size of the input for bounded $p,q$, and also matches the recent $O((\log n/(\log\log n))^{1/p})$-approximation for $(p, \infty)$-Fair Clustering by Makarychev and Vakilian (COLT 2021).

Local Correlation Clustering with Asymmetric Classification Errors

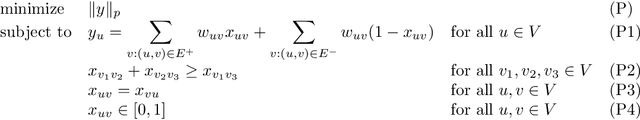
In the Correlation Clustering problem, we are given a complete weighted graph $G$ with its edges labeled as "similar" and "dissimilar" by a noisy binary classifier. For a clustering $\mathcal{C}$ of graph $G$, a similar edge is in disagreement with $\mathcal{C}$, if its endpoints belong to distinct clusters; and a dissimilar edge is in disagreement with $\mathcal{C}$ if its endpoints belong to the same cluster. The disagreements vector, $\text{dis}$, is a vector indexed by the vertices of $G$ such that the $v$-th coordinate $\text{dis}_v$ equals the weight of all disagreeing edges incident on $v$. The goal is to produce a clustering that minimizes the $\ell_p$ norm of the disagreements vector for $p\geq 1$. We study the $\ell_p$ objective in Correlation Clustering under the following assumption: Every similar edge has weight in the range of $[\alpha\mathbf{w},\mathbf{w}]$ and every dissimilar edge has weight at least $\alpha\mathbf{w}$ (where $\alpha \leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give an $O\left((\frac{1}{\alpha})^{\frac{1}{2}-\frac{1}{2p}}\cdot \log\frac{1}{\alpha}\right)$ approximation algorithm for this problem. Furthermore, we show an almost matching convex programming integrality gap.

Correlation Clustering with Asymmetric Classification Errors

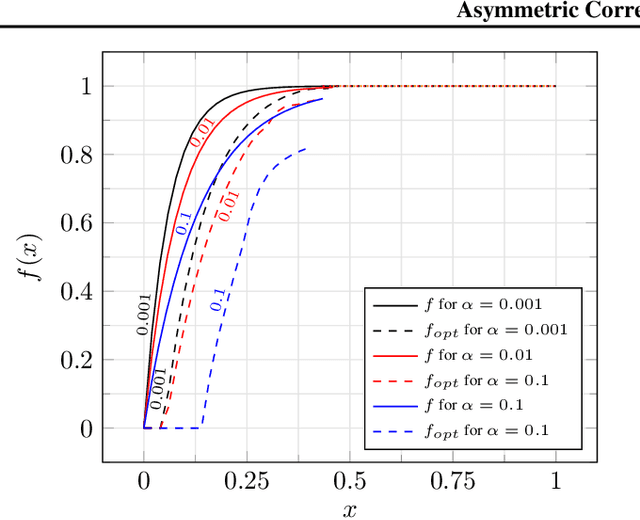
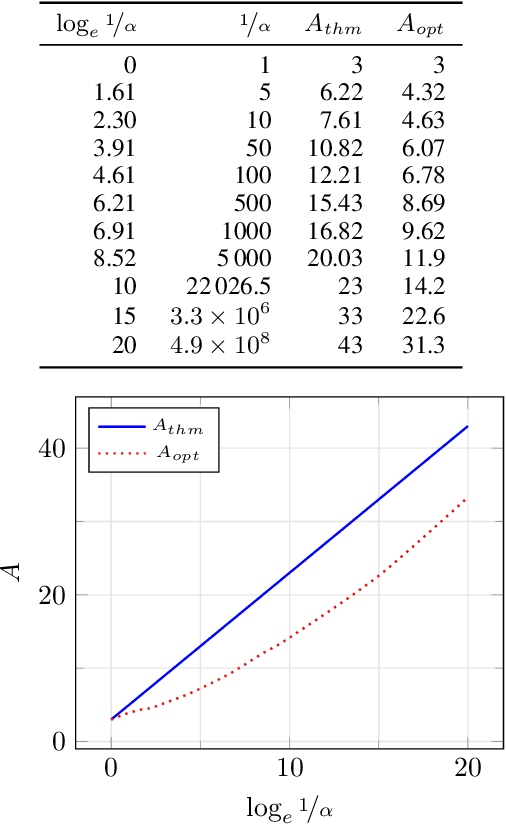
In the Correlation Clustering problem, we are given a weighted graph $G$ with its edges labeled as "similar" or "dissimilar" by a binary classifier. The goal is to produce a clustering that minimizes the weight of "disagreements": the sum of the weights of "similar" edges across clusters and "dissimilar" edges within clusters. We study the correlation clustering problem under the following assumption: Every "similar" edge $e$ has weight $\mathbf{w}_e\in[\alpha \mathbf{w}, \mathbf{w}]$ and every "dissimilar" edge $e$ has weight $\mathbf{w}_e\geq \alpha \mathbf{w}$ (where $\alpha\leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give a $(3 + 2 \log_e (1/\alpha))$ approximation algorithm for this problem. This assumption captures well the scenario when classification errors are asymmetric. Additionally, we show an asymptotically matching Linear Programming integrality gap of $\Omega(\log 1/\alpha)$.

Approximation Algorithms for Socially Fair Clustering

We present an $(e^{O(p)} \frac{\log \ell}{\log\log\ell})$-approximation algorithm for socially fair clustering with the $\ell_p$-objective. In this problem, we are given a set of points in a metric space. Each point belongs to one (or several) of $\ell$ groups. The goal is to find a $k$-medians, $k$-means, or, more generally, $\ell_p$-clustering that is simultaneously good for all of the groups. More precisely, we need to find a set of $k$ centers $C$ so as to minimize the maximum over all groups $j$ of $\sum_{u \text{ in group }j} d(u,C)^p$. The socially fair clustering problem was independently proposed by Abbasi, Bhaskara, and Venkatasubramanian [2021] and Ghadiri, Samadi, and Vempala [2021]. Our algorithm improves and generalizes their $O(\ell)$-approximation algorithms for the problem. The natural LP relaxation for the problem has an integrality gap of $\Omega(\ell)$. In order to obtain our result, we introduce a strengthened LP relaxation and show that it has an integrality gap of $\Theta(\frac{\log \ell}{\log\log\ell})$ for a fixed $p$. Additionally, we present a bicriteria approximation algorithm, which generalizes the bicriteria approximation of Abbasi et al. [2021].

Regression via Kirszbraun Extension with Applications to Imitation Learning

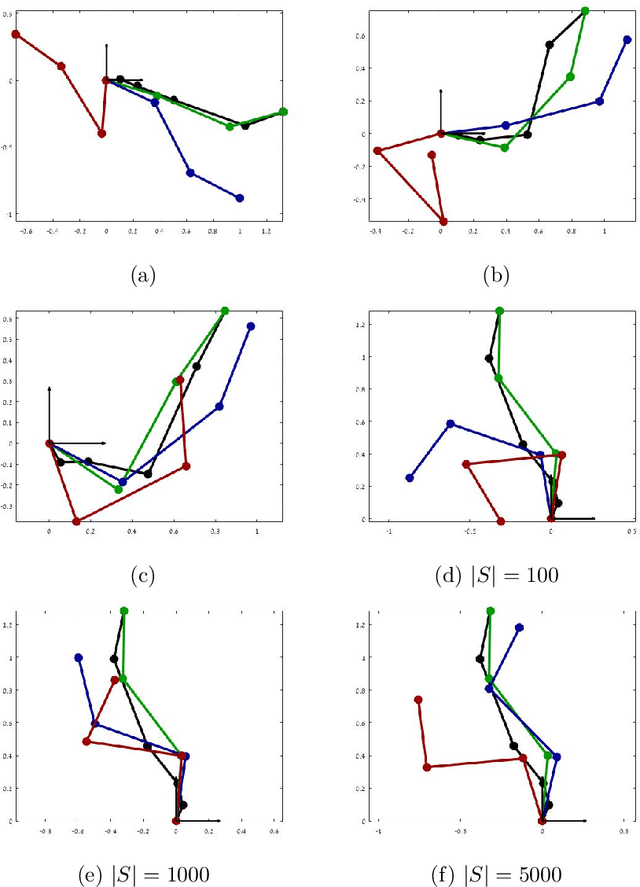
Learning by demonstration is a versatile and rapid mechanism for transferring motor skills from a teacher to a learner. A particular challenge in imitation learning is the so-called correspondence problem, which involves mapping actions between a teacher and a learner having substantially different embodiments (say, human to robot). We present a general, model free and non-parametric imitation learning algorithm based on regression between two Hilbert spaces. We accomplish this via Kirszbraun's extension theorem --- apparently the first application of this technique to supervised learning --- and analyze its statistical and computational aspects. We begin by formulating the correspondence problem in terms of quadratically constrained quadratic program (QCQP) regression. Then we describe a procedure for smoothing the training data, which amounts to regularizing hypothesis complexity via its Lipschitz constant. The Lipschitz constant is tuned via a Structural Risk Minimization (SRM) procedure, based on the covering-number risk bounds we derive. We apply our technique to a static posture imitation task between two robotic manipulators with different embodiments, and report promising results.

Nonlinear Dimension Reduction via Outer Bi-Lipschitz Extensions

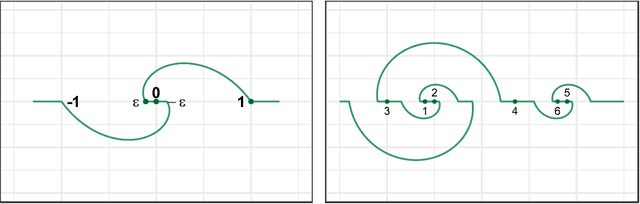
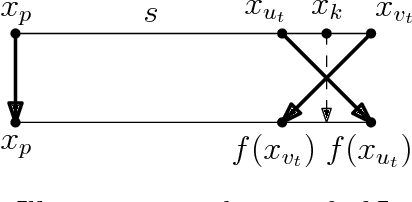
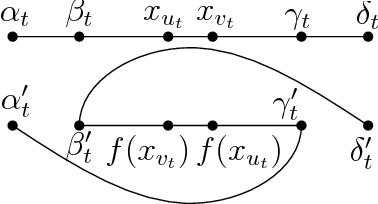
We introduce and study the notion of an outer bi-Lipschitz extension of a map between Euclidean spaces. The notion is a natural analogue of the notion of a Lipschitz extension of a Lipschitz map. We show that for every map $f$ there exists an outer bi-Lipschitz extension $f'$ whose distortion is greater than that of $f$ by at most a constant factor. This result can be seen as a counterpart of the classic Kirszbraun theorem for outer bi-Lipschitz extensions. We also study outer bi-Lipschitz extensions of near-isometric maps and show upper and lower bounds for them. Then, we present applications of our results to prioritized and terminal dimension reduction problems. * We prove a prioritized variant of the Johnson-Lindenstrauss lemma: given a set of points $X\subset \mathbb{R}^d$ of size $N$ and a permutation ("priority ranking") of $X$, there exists an embedding $f$ of $X$ into $\mathbb{R}^{O(\log N)}$ with distortion $O(\log \log N)$ such that the point of rank $j$ has only $O(\log^{3 + \varepsilon} j)$ non-zero coordinates - more specifically, all but the first $O(\log^{3+\varepsilon} j)$ coordinates are equal to $0$; the distortion of $f$ restricted to the first $j$ points (according to the ranking) is at most $O(\log\log j)$. The result makes a progress towards answering an open question by Elkin, Filtser, and Neiman about prioritized dimension reductions. * We prove that given a set $X$ of $N$ points in $\mathbb{R}^d$, there exists a terminal dimension reduction embedding of $\mathbb{R}^d$ into $\mathbb{R}^{d'}$, where $d' = O\left(\frac{\log N}{\varepsilon^4}\right)$, which preserves distances $\|x-y\|$ between points $x\in X$ and $y \in \mathbb{R}^{d}$, up to a multiplicative factor of $1 \pm \varepsilon$. This improves a recent result by Elkin, Filtser, and Neiman. The dimension reductions that we obtain are nonlinear, and this nonlinearity is necessary.

Performance of Johnson-Lindenstrauss Transform for k-Means and k-Medians Clustering

Consider an instance of Euclidean $k$-means or $k$-medians clustering. We show that the cost of the optimal solution is preserved up to a factor of $(1+\varepsilon)$ under a projection onto a random $O(\log(k / \varepsilon) / \varepsilon^2)$-dimensional subspace. Further, the cost of every clustering is preserved within $(1+\varepsilon)$. More generally, our result applies to any dimension reduction map satisfying a mild sub-Gaussian-tail condition. Our bound on the dimension is nearly optimal. Additionally, our result applies to Euclidean $k$-clustering with the distances raised to the $p$-th power for any constant $p$. For $k$-means, our result resolves an open problem posed by Cohen, Elder, Musco, Musco, and Persu (STOC 2015); for $k$-medians, it answers a question raised by Kannan.

Learning Communities in the Presence of Errors

We study the problem of learning communities in the presence of modeling errors and give robust recovery algorithms for the Stochastic Block Model (SBM). This model, which is also known as the Planted Partition Model, is widely used for community detection and graph partitioning in various fields, including machine learning, statistics, and social sciences. Many algorithms exist for learning communities in the Stochastic Block Model, but they do not work well in the presence of errors. In this paper, we initiate the study of robust algorithms for partial recovery in SBM with modeling errors or noise. We consider graphs generated according to the Stochastic Block Model and then modified by an adversary. We allow two types of adversarial errors, Feige---Kilian or monotone errors, and edge outlier errors. Mossel, Neeman and Sly (STOC 2015) posed an open question about whether an almost exact recovery is possible when the adversary is allowed to add $o(n)$ edges. Our work answers this question affirmatively even in the case of $k>2$ communities. We then show that our algorithms work not only when the instances come from SBM, but also work when the instances come from any distribution of graphs that is $\epsilon m$ close to SBM in the Kullback---Leibler divergence. This result also works in the presence of adversarial errors. Finally, we present almost tight lower bounds for two communities.