Four Algorithms for Correlation Clustering: A Survey

In the Correlation Clustering problem, we are given a set of objects with pairwise similarity information. Our aim is to partition these objects into clusters that match this information as closely as possible. More specifically, the pairwise information is given as a weighted graph $G$ with its edges labelled as ``similar" or ``dissimilar" by a binary classifier. The goal is to produce a clustering that minimizes the weight of ``disagreements": the sum of the weights of similar edges across clusters and dissimilar edges within clusters. In this exposition we focus on the case when $G$ is complete and unweighted. We explore four approximation algorithms for the Correlation Clustering problem under this assumption. In particular, we describe the following algorithms: (i) the $17429-$approximation algorithm by Bansal, Blum, and Chawla, (ii) the $4-$approximation algorithm by Charikar, Guruswami, and Wirth (iii) the $3-$approximation algorithm by Ailon, Charikar, and Newman (iv) the $2.06-$approximation algorithm by Chawla, Makarychev, Schramm, and Yaroslavtsev.

Matrix Completion with Sparse Noisy Rows

Exact matrix completion and low rank matrix estimation problems has been studied in different underlying conditions. In this work we study exact low-rank completion under non-degenerate noise model. Non-degenerate random noise model has been previously studied by many researchers under given condition that the noise is sparse and existing in some of the columns. In this paper, we assume that each row can receive random noise instead of columns and propose an interactive algorithm that is robust to this noise. We show that we use a parametrization technique to give a condition when the underlying matrix could be recoverable and suggest an algorithm which recovers the underlying matrix.

Survey of Matrix Completion Algorithms

Matrix completion problem has been investigated under many different conditions since Netflix announced the Netflix Prize problem. Many research work has been done in the field once it has been discovered that many real life dataset could be estimated with a low-rank matrix. Since then compressed sensing, adaptive signal detection has gained the attention of many researchers. In this survey paper we are going to visit some of the matrix completion methods, mainly in the direction of passive and adaptive directions. First, we discuss passive matrix completion methods with convex optimization, and the second active matrix completion techniques with adaptive signal detection methods. Traditionally many machine learning problems are solved in passive environment. However, later it has been observed that adaptive sensing algorithms many times performs more efficiently than former algorithms. Hence algorithms in this setting has been extensively studied. Therefore, we are going to present some of the latest adaptive matrix completion algorithms in this paper meanwhile providing passive methods.

Local Correlation Clustering with Asymmetric Classification Errors

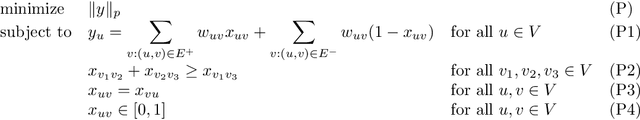
In the Correlation Clustering problem, we are given a complete weighted graph $G$ with its edges labeled as "similar" and "dissimilar" by a noisy binary classifier. For a clustering $\mathcal{C}$ of graph $G$, a similar edge is in disagreement with $\mathcal{C}$, if its endpoints belong to distinct clusters; and a dissimilar edge is in disagreement with $\mathcal{C}$ if its endpoints belong to the same cluster. The disagreements vector, $\text{dis}$, is a vector indexed by the vertices of $G$ such that the $v$-th coordinate $\text{dis}_v$ equals the weight of all disagreeing edges incident on $v$. The goal is to produce a clustering that minimizes the $\ell_p$ norm of the disagreements vector for $p\geq 1$. We study the $\ell_p$ objective in Correlation Clustering under the following assumption: Every similar edge has weight in the range of $[\alpha\mathbf{w},\mathbf{w}]$ and every dissimilar edge has weight at least $\alpha\mathbf{w}$ (where $\alpha \leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give an $O\left((\frac{1}{\alpha})^{\frac{1}{2}-\frac{1}{2p}}\cdot \log\frac{1}{\alpha}\right)$ approximation algorithm for this problem. Furthermore, we show an almost matching convex programming integrality gap.

Correlation Clustering with Asymmetric Classification Errors

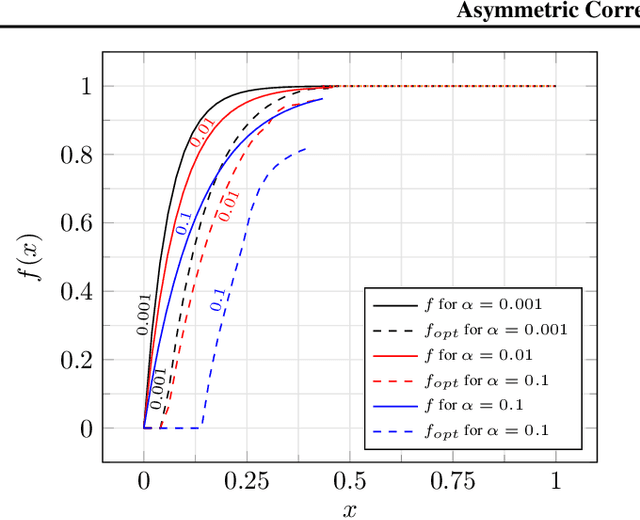
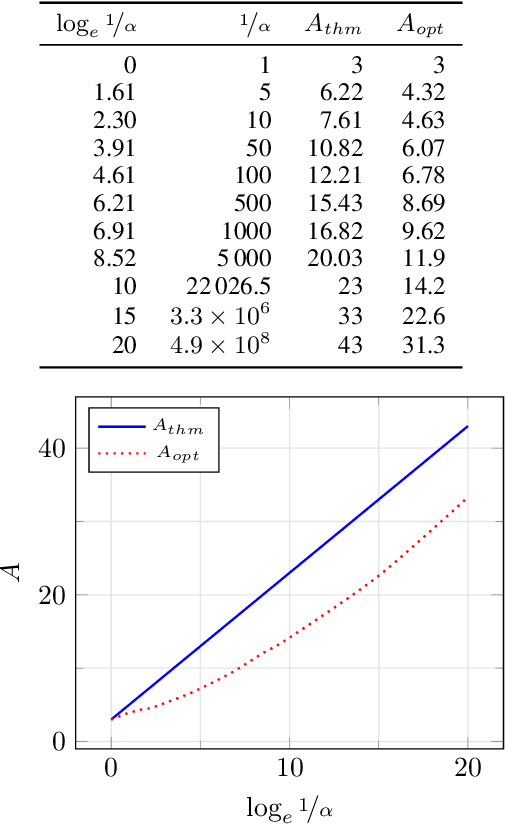
In the Correlation Clustering problem, we are given a weighted graph $G$ with its edges labeled as "similar" or "dissimilar" by a binary classifier. The goal is to produce a clustering that minimizes the weight of "disagreements": the sum of the weights of "similar" edges across clusters and "dissimilar" edges within clusters. We study the correlation clustering problem under the following assumption: Every "similar" edge $e$ has weight $\mathbf{w}_e\in[\alpha \mathbf{w}, \mathbf{w}]$ and every "dissimilar" edge $e$ has weight $\mathbf{w}_e\geq \alpha \mathbf{w}$ (where $\alpha\leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give a $(3 + 2 \log_e (1/\alpha))$ approximation algorithm for this problem. This assumption captures well the scenario when classification errors are asymmetric. Additionally, we show an asymptotically matching Linear Programming integrality gap of $\Omega(\log 1/\alpha)$.