Correlation Clustering with Asymmetric Classification Errors
Paper and Code
Aug 11, 2021
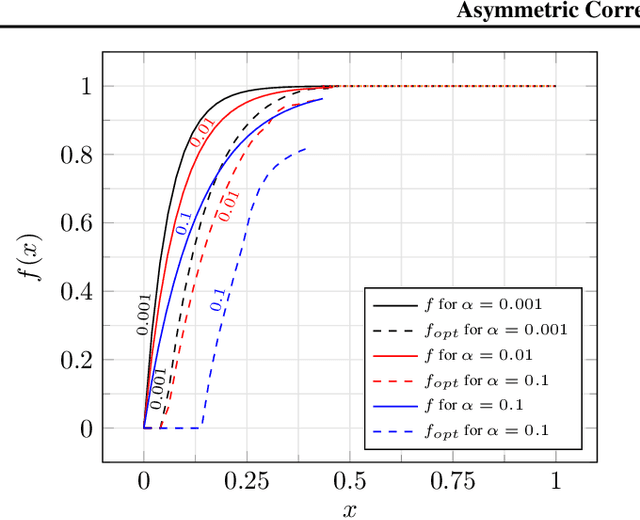
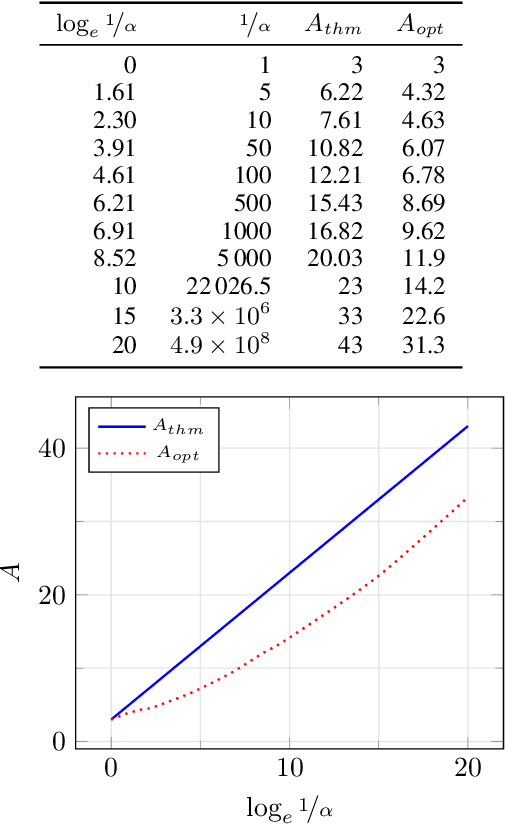
In the Correlation Clustering problem, we are given a weighted graph $G$ with its edges labeled as "similar" or "dissimilar" by a binary classifier. The goal is to produce a clustering that minimizes the weight of "disagreements": the sum of the weights of "similar" edges across clusters and "dissimilar" edges within clusters. We study the correlation clustering problem under the following assumption: Every "similar" edge $e$ has weight $\mathbf{w}_e\in[\alpha \mathbf{w}, \mathbf{w}]$ and every "dissimilar" edge $e$ has weight $\mathbf{w}_e\geq \alpha \mathbf{w}$ (where $\alpha\leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give a $(3 + 2 \log_e (1/\alpha))$ approximation algorithm for this problem. This assumption captures well the scenario when classification errors are asymmetric. Additionally, we show an asymptotically matching Linear Programming integrality gap of $\Omega(\log 1/\alpha)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge