A Polynomial-Time Approximation for Pairwise Fair $k$-Median Clustering
Paper and Code
May 16, 2024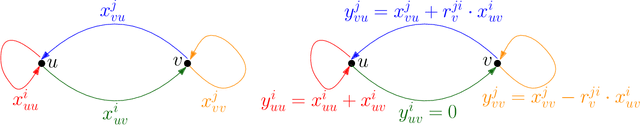
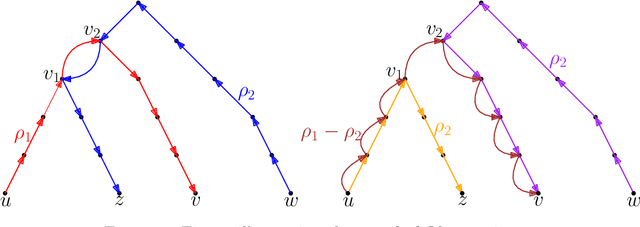
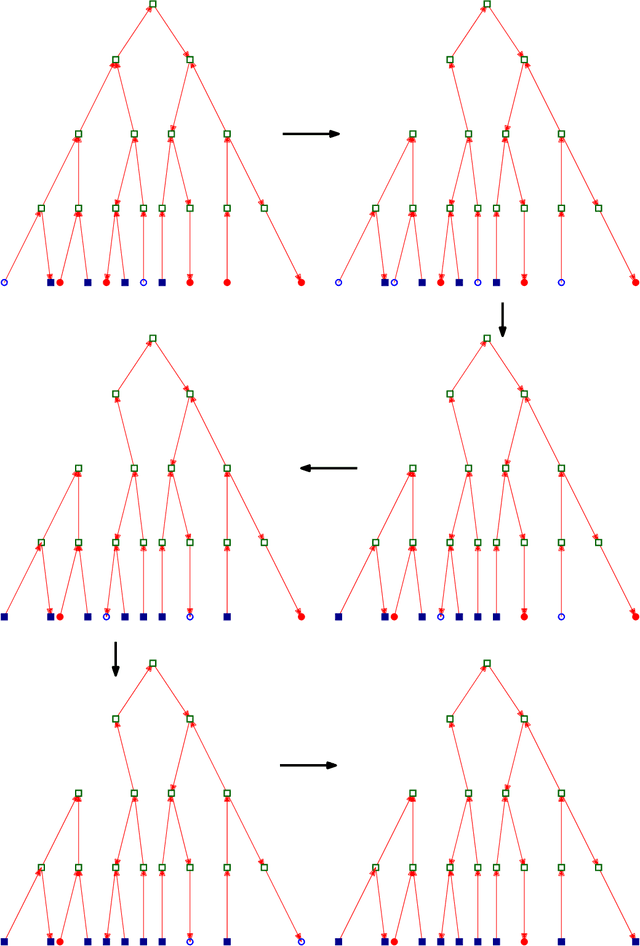
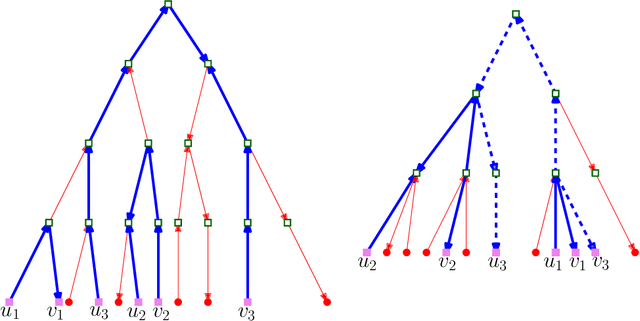
In this work, we study pairwise fair clustering with $\ell \ge 2$ groups, where for every cluster $C$ and every group $i \in [\ell]$, the number of points in $C$ from group $i$ must be at most $t$ times the number of points in $C$ from any other group $j \in [\ell]$, for a given integer $t$. To the best of our knowledge, only bi-criteria approximation and exponential-time algorithms follow for this problem from the prior work on fair clustering problems when $\ell > 2$. In our work, focusing on the $\ell > 2$ case, we design the first polynomial-time $(t^{\ell}\cdot \ell\cdot k)^{O(\ell)}$-approximation for this problem with $k$-median cost that does not violate the fairness constraints. We complement our algorithmic result by providing hardness of approximation results, which show that our problem even when $\ell=2$ is almost as hard as the popular uniform capacitated $k$-median, for which no polynomial-time algorithm with an approximation factor of $o(\log k)$ is known.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge