Fair Summarization: Bridging Quality and Diversity in Extractive Summaries

Fairness in multi-document summarization of user-generated content remains a critical challenge in natural language processing (NLP). Existing summarization methods often fail to ensure equitable representation across different social groups, leading to biased outputs. In this paper, we introduce two novel methods for fair extractive summarization: FairExtract, a clustering-based approach, and FairGPT, which leverages GPT-3.5-turbo with fairness constraints. We evaluate these methods using Divsumm summarization dataset of White-aligned, Hispanic, and African-American dialect tweets and compare them against relevant baselines. The results obtained using a comprehensive set of summarization quality metrics such as SUPERT, BLANC, SummaQA, BARTScore, and UniEval, as well as a fairness metric F, demonstrate that FairExtract and FairGPT achieve superior fairness while maintaining competitive summarization quality. Additionally, we introduce composite metrics (e.g., SUPERT+F, BLANC+F) that integrate quality and fairness into a single evaluation framework, offering a more nuanced understanding of the trade-offs between these objectives. This work highlights the importance of fairness in summarization and sets a benchmark for future research in fairness-aware NLP models.

A Polynomial-Time Approximation for Pairwise Fair $k$-Median Clustering

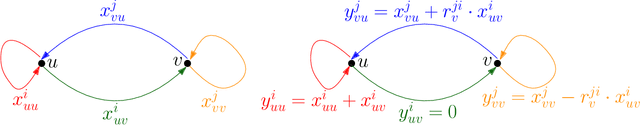
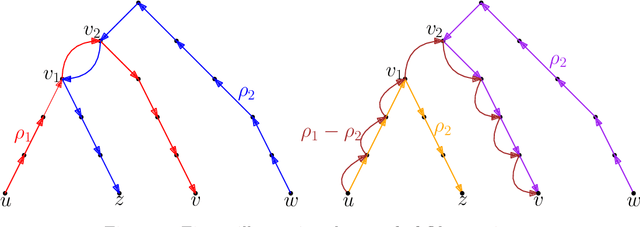
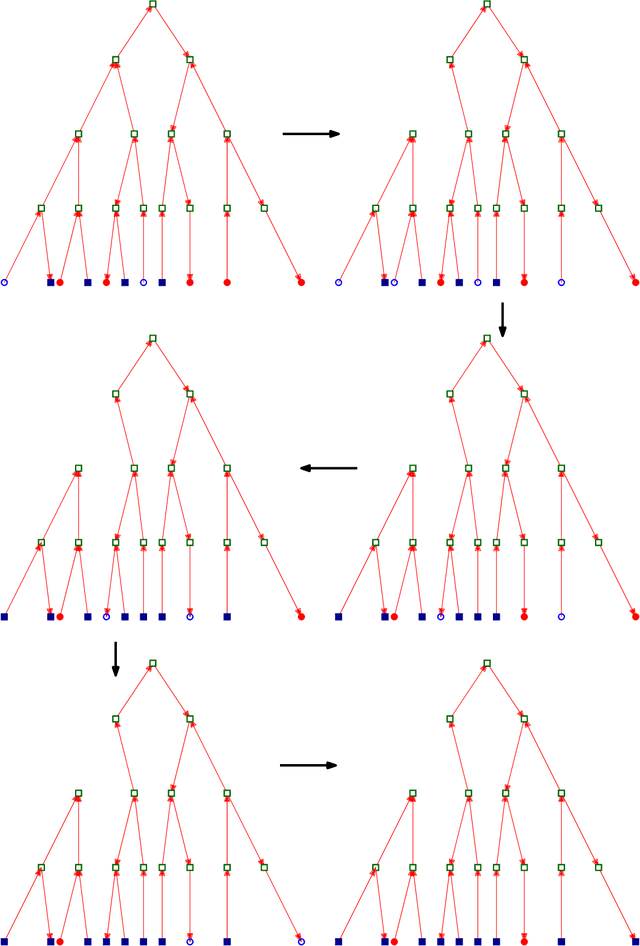
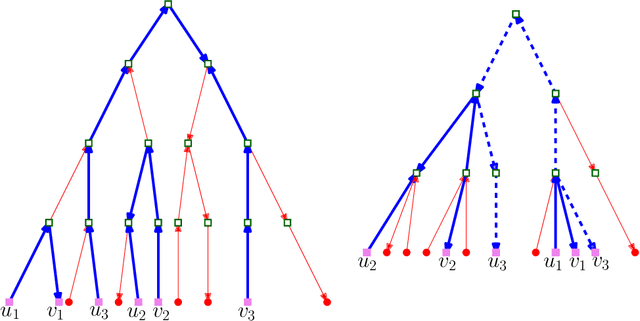
In this work, we study pairwise fair clustering with $\ell \ge 2$ groups, where for every cluster $C$ and every group $i \in [\ell]$, the number of points in $C$ from group $i$ must be at most $t$ times the number of points in $C$ from any other group $j \in [\ell]$, for a given integer $t$. To the best of our knowledge, only bi-criteria approximation and exponential-time algorithms follow for this problem from the prior work on fair clustering problems when $\ell > 2$. In our work, focusing on the $\ell > 2$ case, we design the first polynomial-time $(t^{\ell}\cdot \ell\cdot k)^{O(\ell)}$-approximation for this problem with $k$-median cost that does not violate the fairness constraints. We complement our algorithmic result by providing hardness of approximation results, which show that our problem even when $\ell=2$ is almost as hard as the popular uniform capacitated $k$-median, for which no polynomial-time algorithm with an approximation factor of $o(\log k)$ is known.

How to Find a Good Explanation for Clustering?

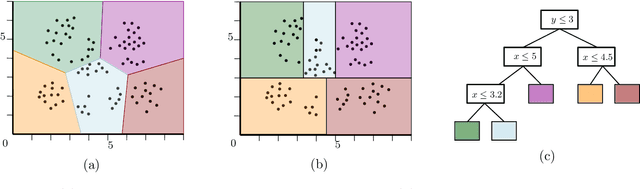
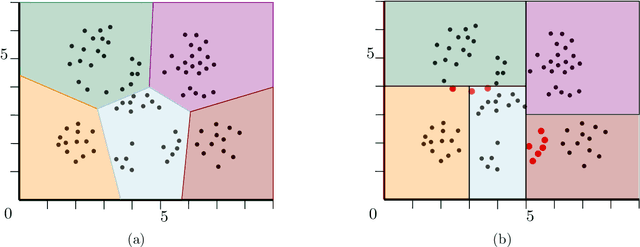
$k$-means and $k$-median clustering are powerful unsupervised machine learning techniques. However, due to complicated dependences on all the features, it is challenging to interpret the resulting cluster assignments. Moshkovitz, Dasgupta, Rashtchian, and Frost [ICML 2020] proposed an elegant model of explainable $k$-means and $k$-median clustering. In this model, a decision tree with $k$ leaves provides a straightforward characterization of the data set into clusters. We study two natural algorithmic questions about explainable clustering. (1) For a given clustering, how to find the "best explanation" by using a decision tree with $k$ leaves? (2) For a given set of points, how to find a decision tree with $k$ leaves minimizing the $k$-means/median objective of the resulting explainable clustering? To address the first question, we introduce a new model of explainable clustering. Our model, inspired by the notion of outliers in robust statistics, is the following. We are seeking a small number of points (outliers) whose removal makes the existing clustering well-explainable. For addressing the second question, we initiate the study of the model of Moshkovitz et al. from the perspective of multivariate complexity. Our rigorous algorithmic analysis sheds some light on the influence of parameters like the input size, dimension of the data, the number of outliers, the number of clusters, and the approximation ratio, on the computational complexity of explainable clustering.

On Coresets for Fair Clustering in Metric and Euclidean Spaces and Their Applications

Fair clustering is a constrained variant of clustering where the goal is to partition a set of colored points, such that the fraction of points of any color in every cluster is more or less equal to the fraction of points of this color in the dataset. This variant was recently introduced by Chierichetti et al. [NeurIPS, 2017] in a seminal work and became widely popular in the clustering literature. In this paper, we propose a new construction of coresets for fair clustering based on random sampling. The new construction allows us to obtain the first coreset for fair clustering in general metric spaces. For Euclidean spaces, we obtain the first coreset whose size does not depend exponentially on the dimension. Our coreset results solve open questions proposed by Schmidt et al. [WAOA, 2019] and Huang et al. [NeurIPS, 2019]. The new coreset construction helps to design several new approximation and streaming algorithms. In particular, we obtain the first true constant-approximation algorithm for metric fair clustering, whose running time is fixed-parameter tractable (FPT). In the Euclidean case, we derive the first $(1+\epsilon)$-approximation algorithm for fair clustering whose time complexity is near-linear and does not depend exponentially on the dimension of the space. Besides, our coreset construction scheme is fairly general and gives rise to coresets for a wide range of constrained clustering problems. This leads to improved constant-approximations for these problems in general metrics and near-linear time $(1+\epsilon)$-approximations in the Euclidean metric.