How to Find a Good Explanation for Clustering?

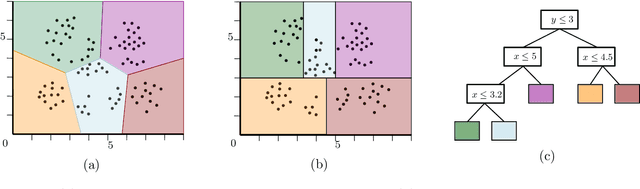
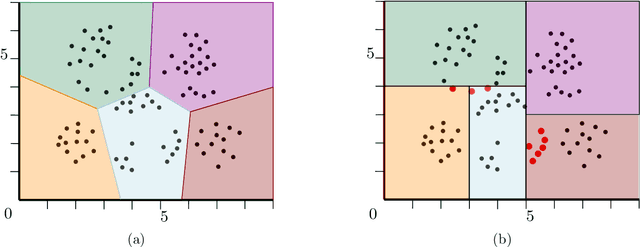
$k$-means and $k$-median clustering are powerful unsupervised machine learning techniques. However, due to complicated dependences on all the features, it is challenging to interpret the resulting cluster assignments. Moshkovitz, Dasgupta, Rashtchian, and Frost [ICML 2020] proposed an elegant model of explainable $k$-means and $k$-median clustering. In this model, a decision tree with $k$ leaves provides a straightforward characterization of the data set into clusters. We study two natural algorithmic questions about explainable clustering. (1) For a given clustering, how to find the "best explanation" by using a decision tree with $k$ leaves? (2) For a given set of points, how to find a decision tree with $k$ leaves minimizing the $k$-means/median objective of the resulting explainable clustering? To address the first question, we introduce a new model of explainable clustering. Our model, inspired by the notion of outliers in robust statistics, is the following. We are seeking a small number of points (outliers) whose removal makes the existing clustering well-explainable. For addressing the second question, we initiate the study of the model of Moshkovitz et al. from the perspective of multivariate complexity. Our rigorous algorithmic analysis sheds some light on the influence of parameters like the input size, dimension of the data, the number of outliers, the number of clusters, and the approximation ratio, on the computational complexity of explainable clustering.

Present-Biased Optimization

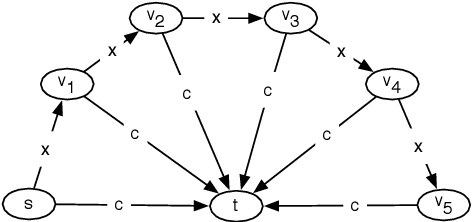
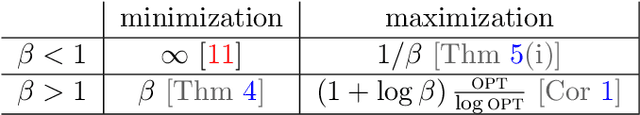
This paper explores the behavior of present-biased agents, that is, agents who erroneously anticipate the costs of future actions compared to their real costs. Specifically, the paper extends the original framework proposed by Akerlof (1991) for studying various aspects of human behavior related to time-inconsistent planning, including procrastination, and abandonment, as well as the elegant graph-theoretic model encapsulating this framework recently proposed by Kleinberg and Oren (2014). The benefit of this extension is twofold. First, it enables to perform fine grained analysis of the behavior of present-biased agents depending on the optimisation task they have to perform. In particular, we study covering tasks vs. hitting tasks, and show that the ratio between the cost of the solutions computed by present-biased agents and the cost of the optimal solutions may differ significantly depending on the problem constraints. Second, our extension enables to study not only underestimation of future costs, coupled with minimization problems, but also all combinations of minimization/maximization, and underestimation/overestimation. We study the four scenarios, and we establish upper bounds on the cost ratio for three of them (the cost ratio for the original scenario was known to be unbounded), providing a complete global picture of the behavior of present-biased agents, as far as optimisation tasks are concerned.

EPTAS for $k$-means Clustering of Affine Subspaces

We consider a generalization of the fundamental $k$-means clustering for data with incomplete or corrupted entries. When data objects are represented by points in $\mathbb{R}^d$, a data point is said to be incomplete when some of its entries are missing or unspecified. An incomplete data point with at most $\Delta$ unspecified entries corresponds to an axis-parallel affine subspace of dimension at most $\Delta$, called a $\Delta$-point. Thus we seek a partition of $n$ input $\Delta$-points into $k$ clusters minimizing the $k$-means objective. For $\Delta=0$, when all coordinates of each point are specified, this is the usual $k$-means clustering. We give an algorithm that finds an $(1+ \epsilon)$-approximate solution in time $f(k,\epsilon, \Delta) \cdot n^2 \cdot d$ for some function $f$ of $k,\epsilon$, and $\Delta$ only.

Refined Complexity of PCA with Outliers

Principal component analysis (PCA) is one of the most fundamental procedures in exploratory data analysis and is the basic step in applications ranging from quantitative finance and bioinformatics to image analysis and neuroscience. However, it is well-documented that the applicability of PCA in many real scenarios could be constrained by an "immune deficiency" to outliers such as corrupted observations. We consider the following algorithmic question about the PCA with outliers. For a set of $n$ points in $\mathbb{R}^{d}$, how to learn a subset of points, say 1% of the total number of points, such that the remaining part of the points is best fit into some unknown $r$-dimensional subspace? We provide a rigorous algorithmic analysis of the problem. We show that the problem is solvable in time $n^{O(d^2)}$. In particular, for constant dimension the problem is solvable in polynomial time. We complement the algorithmic result by the lower bound, showing that unless Exponential Time Hypothesis fails, in time $f(d)n^{o(d)}$, for any function $f$ of $d$, it is impossible not only to solve the problem exactly but even to approximate it within a constant factor.

Approximation Schemes for Low-Rank Binary Matrix Approximation Problems

We provide a randomized linear time approximation scheme for a generic problem about clustering of binary vectors subject to additional constrains. The new constrained clustering problem encompasses a number of problems and by solving it, we obtain the first linear time-approximation schemes for a number of well-studied fundamental problems concerning clustering of binary vectors and low-rank approximation of binary matrices. Among the problems solvable by our approach are \textsc{Low GF(2)-Rank Approximation}, \textsc{Low Boolean-Rank Approximation}, and various versions of \textsc{Binary Clustering}. For example, for \textsc{Low GF(2)-Rank Approximation} problem, where for an $m\times n$ binary matrix $A$ and integer $r>0$, we seek for a binary matrix $B$ of $GF_2$ rank at most $r$ such that $\ell_0$ norm of matrix $A-B$ is minimum, our algorithm, for any $\epsilon>0$ in time $ f(r,\epsilon)\cdot n\cdot m$, where $f$ is some computable function, outputs a $(1+\epsilon)$-approximate solution with probability at least $(1-\frac{1}{e})$. Our approximation algorithms substantially improve the running times and approximation factors of previous works. We also give (deterministic) PTASes for these problems running in time $n^{f(r)\frac{1}{\epsilon^2}\log \frac{1}{\epsilon}}$, where $f$ is some function depending on the problem. Our algorithm for the constrained clustering problem is based on a novel sampling lemma, which is interesting in its own.