Solving Quantified Boolean Formulas with Few Existential Variables

The quantified Boolean formula (QBF) problem is an important decision problem generally viewed as the archetype for PSPACE-completeness. Many problems of central interest in AI are in general not included in NP, e.g., planning, model checking, and non-monotonic reasoning, and for such problems QBF has successfully been used as a modelling tool. However, solvers for QBF are not as advanced as state of the art SAT solvers, which has prevented QBF from becoming a universal modelling language for PSPACE-complete problems. A theoretical explanation is that QBF (as well as many other PSPACE-complete problems) lacks natural parameters} guaranteeing fixed-parameter tractability (FPT). In this paper we tackle this problem and consider a simple but overlooked parameter: the number of existentially quantified variables. This natural parameter is virtually unexplored in the literature which one might find surprising given the general scarcity of FPT algorithms for QBF. Via this parameterization we then develop a novel FPT algorithm applicable to QBF instances in conjunctive normal form (CNF) of bounded clause length. We complement this by a W[1]-hardness result for QBF in CNF of unbounded clause length as well as sharper lower bounds for the bounded arity case under the (strong) exponential-time hypothesis.

Boolean and $\mathbb{F}_p$-Matrix Factorization: From Theory to Practice

Boolean Matrix Factorization (BMF) aims to find an approximation of a given binary matrix as the Boolean product of two low-rank binary matrices. Binary data is ubiquitous in many fields, and representing data by binary matrices is common in medicine, natural language processing, bioinformatics, computer graphics, among many others. Unfortunately, BMF is computationally hard and heuristic algorithms are used to compute Boolean factorizations. Very recently, the theoretical breakthrough was obtained independently by two research groups. Ban et al. (SODA 2019) and Fomin et al. (Trans. Algorithms 2020) show that BMF admits an efficient polynomial-time approximation scheme (EPTAS). However, despite the theoretical importance, the high double-exponential dependence of the running times from the rank makes these algorithms unimplementable in practice. The primary research question motivating our work is whether the theoretical advances on BMF could lead to practical algorithms. The main conceptional contribution of our work is the following. While EPTAS for BMF is a purely theoretical advance, the general approach behind these algorithms could serve as the basis in designing better heuristics. We also use this strategy to develop new algorithms for related $\mathbb{F}_p$-Matrix Factorization. Here, given a matrix $A$ over a finite field GF($p$) where $p$ is a prime, and an integer $r$, our objective is to find a matrix $B$ over the same field with GF($p$)-rank at most $r$ minimizing some norm of $A-B$. Our empirical research on synthetic and real-world data demonstrates the advantage of the new algorithms over previous works on BMF and $\mathbb{F}_p$-Matrix Factorization.

EPTAS for $k$-means Clustering of Affine Subspaces

We consider a generalization of the fundamental $k$-means clustering for data with incomplete or corrupted entries. When data objects are represented by points in $\mathbb{R}^d$, a data point is said to be incomplete when some of its entries are missing or unspecified. An incomplete data point with at most $\Delta$ unspecified entries corresponds to an axis-parallel affine subspace of dimension at most $\Delta$, called a $\Delta$-point. Thus we seek a partition of $n$ input $\Delta$-points into $k$ clusters minimizing the $k$-means objective. For $\Delta=0$, when all coordinates of each point are specified, this is the usual $k$-means clustering. We give an algorithm that finds an $(1+ \epsilon)$-approximate solution in time $f(k,\epsilon, \Delta) \cdot n^2 \cdot d$ for some function $f$ of $k,\epsilon$, and $\Delta$ only.

Refined Complexity of PCA with Outliers

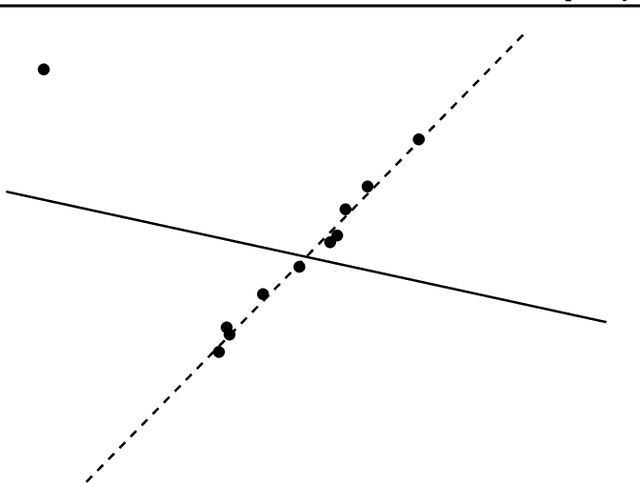
Principal component analysis (PCA) is one of the most fundamental procedures in exploratory data analysis and is the basic step in applications ranging from quantitative finance and bioinformatics to image analysis and neuroscience. However, it is well-documented that the applicability of PCA in many real scenarios could be constrained by an "immune deficiency" to outliers such as corrupted observations. We consider the following algorithmic question about the PCA with outliers. For a set of $n$ points in $\mathbb{R}^{d}$, how to learn a subset of points, say 1% of the total number of points, such that the remaining part of the points is best fit into some unknown $r$-dimensional subspace? We provide a rigorous algorithmic analysis of the problem. We show that the problem is solvable in time $n^{O(d^2)}$. In particular, for constant dimension the problem is solvable in polynomial time. We complement the algorithmic result by the lower bound, showing that unless Exponential Time Hypothesis fails, in time $f(d)n^{o(d)}$, for any function $f$ of $d$, it is impossible not only to solve the problem exactly but even to approximate it within a constant factor.

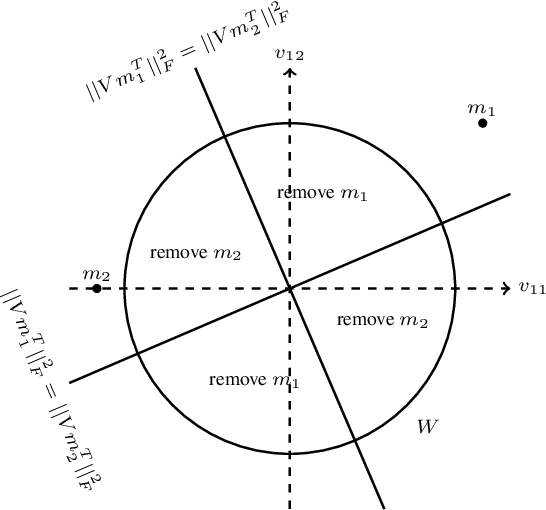
Approximation Schemes for Low-Rank Binary Matrix Approximation Problems

We provide a randomized linear time approximation scheme for a generic problem about clustering of binary vectors subject to additional constrains. The new constrained clustering problem encompasses a number of problems and by solving it, we obtain the first linear time-approximation schemes for a number of well-studied fundamental problems concerning clustering of binary vectors and low-rank approximation of binary matrices. Among the problems solvable by our approach are \textsc{Low GF(2)-Rank Approximation}, \textsc{Low Boolean-Rank Approximation}, and various versions of \textsc{Binary Clustering}. For example, for \textsc{Low GF(2)-Rank Approximation} problem, where for an $m\times n$ binary matrix $A$ and integer $r>0$, we seek for a binary matrix $B$ of $GF_2$ rank at most $r$ such that $\ell_0$ norm of matrix $A-B$ is minimum, our algorithm, for any $\epsilon>0$ in time $ f(r,\epsilon)\cdot n\cdot m$, where $f$ is some computable function, outputs a $(1+\epsilon)$-approximate solution with probability at least $(1-\frac{1}{e})$. Our approximation algorithms substantially improve the running times and approximation factors of previous works. We also give (deterministic) PTASes for these problems running in time $n^{f(r)\frac{1}{\epsilon^2}\log \frac{1}{\epsilon}}$, where $f$ is some function depending on the problem. Our algorithm for the constrained clustering problem is based on a novel sampling lemma, which is interesting in its own.