CSPs with Few Alien Constraints

The constraint satisfaction problem asks to decide if a set of constraints over a relational structure $\mathcal{A}$ is satisfiable (CSP$(\mathcal{A})$). We consider CSP$(\mathcal{A} \cup \mathcal{B})$ where $\mathcal{A}$ is a structure and $\mathcal{B}$ is an alien structure, and analyse its (parameterized) complexity when at most $k$ alien constraints are allowed. We establish connections and obtain transferable complexity results to several well-studied problems that previously escaped classification attempts. Our novel approach, utilizing logical and algebraic methods, yields an FPT versus pNP dichotomy for arbitrary finite structures and sharper dichotomies for Boolean structures and first-order reducts of $(\mathbb{N},=)$ (equality CSPs), together with many partial results for general $\omega$-categorical structures.

Solving Quantified Boolean Formulas with Few Existential Variables

The quantified Boolean formula (QBF) problem is an important decision problem generally viewed as the archetype for PSPACE-completeness. Many problems of central interest in AI are in general not included in NP, e.g., planning, model checking, and non-monotonic reasoning, and for such problems QBF has successfully been used as a modelling tool. However, solvers for QBF are not as advanced as state of the art SAT solvers, which has prevented QBF from becoming a universal modelling language for PSPACE-complete problems. A theoretical explanation is that QBF (as well as many other PSPACE-complete problems) lacks natural parameters} guaranteeing fixed-parameter tractability (FPT). In this paper we tackle this problem and consider a simple but overlooked parameter: the number of existentially quantified variables. This natural parameter is virtually unexplored in the literature which one might find surprising given the general scarcity of FPT algorithms for QBF. Via this parameterization we then develop a novel FPT algorithm applicable to QBF instances in conjunctive normal form (CNF) of bounded clause length. We complement this by a W[1]-hardness result for QBF in CNF of unbounded clause length as well as sharper lower bounds for the bounded arity case under the (strong) exponential-time hypothesis.

Improved Algorithms for Allen's Interval Algebra by Dynamic Programming with Sublinear Partitioning

Allen's interval algebra is one of the most well-known calculi in qualitative temporal reasoning with numerous applications in artificial intelligence. Recently, there has been a surge of improvements in the fine-grained complexity of NP-hard reasoning tasks, improving the running time from the naive $2^{O(n^2)}$ to $O^*((1.0615n)^{n})$, with even faster algorithms for unit intervals a bounded number of overlapping intervals (the $O^*(\cdot)$ notation suppresses polynomial factors). Despite these improvements the best known lower bound is still only $2^{o(n)}$ (under the exponential-time hypothesis) and major improvements in either direction seemingly require fundamental advances in computational complexity. In this paper we propose a novel framework for solving NP-hard qualitative reasoning problems which we refer to as dynamic programming with sublinear partitioning. Using this technique we obtain a major improvement of $O^*((\frac{cn}{\log{n}})^{n})$ for Allen's interval algebra. To demonstrate that the technique is applicable to more domains we apply it to a problem in qualitative spatial reasoning, the cardinal direction point algebra, and solve it in $O^*((\frac{cn}{\log{n}})^{2n/3})$ time. Hence, not only do we significantly advance the state-of-the-art for NP-hard qualitative reasoning problems, but obtain a novel algorithmic technique that is likely applicable to many problems where $2^{O(n)}$ time algorithms are unlikely.

A Fast Algorithm for Consistency Checking Partially Ordered Time

Partially ordered models of time occur naturally in applications where agents or processes cannot perfectly communicate with each other, and can be traced back to the seminal work of Lamport. In this paper we consider the problem of deciding if a (likely incomplete) description of a system of events is consistent, the network consistency problem for the point algebra of partially ordered time (POT). While the classical complexity of this problem has been fully settled, comparably little is known of the fine-grained complexity of POT except that it can be solved in $O^*((0.368n)^n)$ time by enumerating ordered partitions. We construct a much faster algorithm with a run-time bounded by $O^*((0.26n)^n)$. This is achieved by a sophisticated enumeration of structures similar to total orders, which are then greedily expanded toward a solution. While similar ideas have been explored earlier for related problems it turns out that the analysis for POT is non-trivial and requires significant new ideas.

Computational Short Cuts in Infinite Domain Constraint Satisfaction

A backdoor in a finite-domain CSP instance is a set of variables where each possible instantiation moves the instance into a polynomial-time solvable class. Backdoors have found many applications in artificial intelligence and elsewhere, and the algorithmic problem of finding such backdoors has consequently been intensively studied. Sioutis and Janhunen (Proc. 42nd German Conference on AI (KI-2019)) have proposed a generalised backdoor concept suitable for infinite-domain CSP instances over binary constraints. We generalise their concept into a large class of CSPs that allow for higher-arity constraints. We show that this kind of infinite-domain backdoors have many of the positive computational properties that finite-domain backdoors have: the associated computational problems are fixed-parameter tractable whenever the underlying constraint language is finite. On the other hand, we show that infinite languages make the problems considerably harder: the general backdoor detection problem is W[2]-hard and fixed-parameter tractability is ruled out under standard complexity-theoretic assumptions. We demonstrate that backdoors may have suboptimal behaviour on binary constraints -- this is detrimental from an AI perspective where binary constraints are predominant in, for instance, spatiotemporal applications. In response to this, we introduce sidedoors as an alternative to backdoors. The fundamental computational problems for sidedoors remain fixed-parameter tractable for finite constraint language (possibly also containing non-binary relations). Moreover, the sidedoor approach has appealing computational properties that sometimes leads to faster algorithms than the backdoor approach.

A Multivariate Complexity Analysis of Qualitative Reasoning Problems

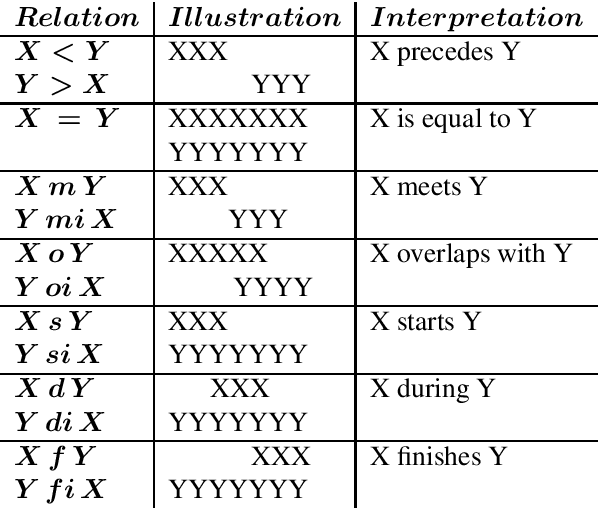
Qualitative reasoning is an important subfield of artificial intelligence where one describes relationships with qualitative, rather than numerical, relations. Many such reasoning tasks, e.g., Allen's interval algebra, can be solved in $2^{O(n \cdot \log n)}$ time, but single-exponential running times $2^{O(n)}$ are currently far out of reach. In this paper we consider single-exponential algorithms via a multivariate analysis consisting of a fine-grained parameter $n$ (e.g., the number of variables) and a coarse-grained parameter $k$ expected to be relatively small. We introduce the classes FPE and XE of problems solvable in $f(k) \cdot 2^{O(n)}$, respectively $f(k)^n$, time, and prove several fundamental properties of these classes. We proceed by studying temporal reasoning problems and (1) show that the Partially Ordered Time problem of effective width $k$ is solvable in $16^{kn}$ time and is thus included in XE, and (2) that the network consistency problem for Allen's interval algebra with no interval overlapping with more than $k$ others is solvable in $(2nk)^{2k} \cdot 2^{n}$ time and is included in FPE. Our multivariate approach is in no way limited to these to specific problems and may be a generally useful approach for obtaining single-exponential algorithms.