Can You Tell the Difference? Contrastive Explanations for ABox Entailments

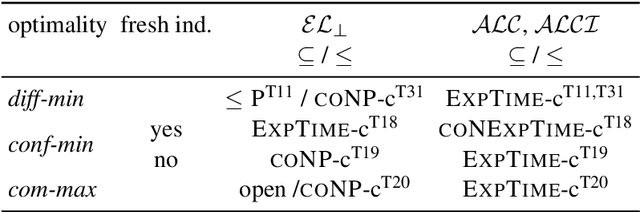
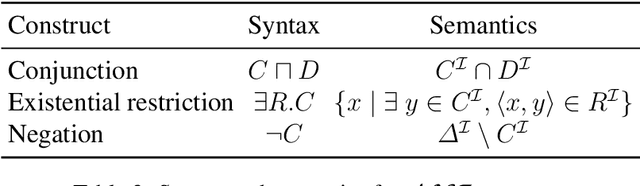
We introduce the notion of contrastive ABox explanations to answer questions of the type "Why is a an instance of C, but b is not?". While there are various approaches for explaining positive entailments (why is C(a) entailed by the knowledge base) as well as missing entailments (why is C(b) not entailed) in isolation, contrastive explanations consider both at the same time, which allows them to focus on the relevant commonalities and differences between a and b. We develop an appropriate notion of contrastive explanations for the special case of ABox reasoning with description logic ontologies, and analyze the computational complexity for different variants under different optimality criteria, considering lightweight as well as more expressive description logics. We implemented a first method for computing one variant of contrastive explanations, and evaluated it on generated problems for realistic knowledge bases.

Structure-Aware Encodings of Argumentation Properties for Clique-width

Structural measures of graphs, such as treewidth, are central tools in computational complexity resulting in efficient algorithms when exploiting the parameter. It is even known that modern SAT solvers work efficiently on instances of small treewidth. Since these solvers are widely applied, research interests in compact encodings into (Q)SAT for solving and to understand encoding limitations. Even more general is the graph parameter clique-width, which unlike treewidth can be small for dense graphs. Although algorithms are available for clique-width, little is known about encodings. We initiate the quest to understand encoding capabilities with clique-width by considering abstract argumentation, which is a robust framework for reasoning with conflicting arguments. It is based on directed graphs and asks for computationally challenging properties, making it a natural candidate to study computational properties. We design novel reductions from argumentation problems to (Q)SAT. Our reductions linearly preserve the clique-width, resulting in directed decomposition-guided (DDG) reductions. We establish novel results for all argumentation semantics, including counting. Notably, the overhead caused by our DDG reductions cannot be significantly improved under reasonable assumptions.

Neural Reasoning for Robust Instance Retrieval in $\mathcal{SHOIQ}$

Concept learning exploits background knowledge in the form of description logic axioms to learn explainable classification models from knowledge bases. Despite recent breakthroughs in neuro-symbolic concept learning, most approaches still cannot be deployed on real-world knowledge bases. This is due to their use of description logic reasoners, which are not robust against inconsistencies nor erroneous data. We address this challenge by presenting a novel neural reasoner dubbed EBR. Our reasoner relies on embeddings to approximate the results of a symbolic reasoner. We show that EBR solely requires retrieving instances for atomic concepts and existential restrictions to retrieve or approximate the set of instances of any concept in the description logic $\mathcal{SHOIQ}$. In our experiments, we compare EBR with state-of-the-art reasoners. Our results suggest that EBR is robust against missing and erroneous data in contrast to existing reasoners.

Facets in Argumentation: A Formal Approach to Argument Significance

Argumentation is a central subarea of Artificial Intelligence (AI) for modeling and reasoning about arguments. The semantics of abstract argumentation frameworks (AFs) is given by sets of arguments (extensions) and conditions on the relationship between them, such as stable or admissible. Today's solvers implement tasks such as finding extensions, deciding credulous or skeptical acceptance, counting, or enumerating extensions. While these tasks are well charted, the area between decision, counting/enumeration and fine-grained reasoning requires expensive reasoning so far. We introduce a novel concept (facets) for reasoning between decision and enumeration. Facets are arguments that belong to some extensions (credulous) but not to all extensions (skeptical). They are most natural when a user aims to navigate, filter, or comprehend the significance of specific arguments, according to their needs. We study the complexity and show that tasks involving facets are much easier than counting extensions. Finally, we provide an implementation, and conduct experiments to demonstrate feasibility.

Loss Functions in Deep Learning: A Comprehensive Review

Loss functions are at the heart of deep learning, shaping how models learn and perform across diverse tasks. They are used to quantify the difference between predicted outputs and ground truth labels, guiding the optimization process to minimize errors. Selecting the right loss function is critical, as it directly impacts model convergence, generalization, and overall performance across various applications, from computer vision to time series forecasting. This paper presents a comprehensive review of loss functions, covering fundamental metrics like Mean Squared Error and Cross-Entropy to advanced functions such as Adversarial and Diffusion losses. We explore their mathematical foundations, impact on model training, and strategic selection for various applications, including computer vision (Discriminative and generative), tabular data prediction, and time series forecasting. For each of these categories, we discuss the most used loss functions in the recent advancements of deep learning techniques. Also, this review explore the historical evolution, computational efficiency, and ongoing challenges in loss function design, underlining the need for more adaptive and robust solutions. Emphasis is placed on complex scenarios involving multi-modal data, class imbalances, and real-world constraints. Finally, we identify key future directions, advocating for loss functions that enhance interpretability, scalability, and generalization, leading to more effective and resilient deep learning models.

Rejection in Abstract Argumentation: Harder Than Acceptance?

Abstract argumentation is a popular toolkit for modeling, evaluating, and comparing arguments. Relationships between arguments are specified in argumentation frameworks (AFs), and conditions are placed on sets (extensions) of arguments that allow AFs to be evaluated. For more expressiveness, AFs are augmented with \emph{acceptance conditions} on directly interacting arguments or a constraint on the admissible sets of arguments, resulting in dialectic frameworks or constrained argumentation frameworks. In this paper, we consider flexible conditions for \emph{rejecting} an argument from an extension, which we call rejection conditions (RCs). On the technical level, we associate each argument with a specific logic program. We analyze the resulting complexity, including the structural parameter treewidth. Rejection AFs are highly expressive, giving rise to natural problems on higher levels of the polynomial hierarchy.

Parameterized Complexity of Logic-Based Argumentation in Schaefer's Framework

Logic-based argumentation is a well-established formalism modelling nonmonotonic reasoning. It has been playing a major role in AI for decades, now. Informally, a set of formulas is the support for a given claim if it is consistent, subset-minimal, and implies the claim. In such a case, the pair of the support and the claim together is called an argument. In this paper, we study the propositional variants of the following three computational tasks studied in argumentation: ARG (exists a support for a given claim with respect to a given set of formulas), ARG-Check (is a given set a support for a given claim), and ARG-Rel (similarly as ARG plus requiring an additionally given formula to be contained in the support). ARG-Check is complete for the complexity class DP, and the other two problems are known to be complete for the second level of the polynomial hierarchy (Parson et al., J. Log. Comput., 2003) and, accordingly, are highly intractable. Analyzing the reason for this intractability, we perform a two-dimensional classification: first, we consider all possible propositional fragments of the problem within Schaefer's framework (STOC 1978), and then study different parameterizations for each of the fragment. We identify a list of reasonable structural parameters (size of the claim, support, knowledge-base) that are connected to the aforementioned decision problems. Eventually, we thoroughly draw a fine border of parameterized intractability for each of the problems showing where the problems are fixed-parameter tractable and when this exactly stops. Surprisingly, several cases are of very high intractability (paraNP and beyond).