Explaining Decisions in ML Models: a Parameterized Complexity Analysis

This paper presents a comprehensive theoretical investigation into the parameterized complexity of explanation problems in various machine learning (ML) models. Contrary to the prevalent black-box perception, our study focuses on models with transparent internal mechanisms. We address two principal types of explanation problems: abductive and contrastive, both in their local and global variants. Our analysis encompasses diverse ML models, including Decision Trees, Decision Sets, Decision Lists, Ordered Binary Decision Diagrams, Random Forests, and Boolean Circuits, and ensembles thereof, each offering unique explanatory challenges. This research fills a significant gap in explainable AI (XAI) by providing a foundational understanding of the complexities of generating explanations for these models. This work provides insights vital for further research in the domain of XAI, contributing to the broader discourse on the necessity of transparency and accountability in AI systems.

Solving Quantified Boolean Formulas with Few Existential Variables

The quantified Boolean formula (QBF) problem is an important decision problem generally viewed as the archetype for PSPACE-completeness. Many problems of central interest in AI are in general not included in NP, e.g., planning, model checking, and non-monotonic reasoning, and for such problems QBF has successfully been used as a modelling tool. However, solvers for QBF are not as advanced as state of the art SAT solvers, which has prevented QBF from becoming a universal modelling language for PSPACE-complete problems. A theoretical explanation is that QBF (as well as many other PSPACE-complete problems) lacks natural parameters} guaranteeing fixed-parameter tractability (FPT). In this paper we tackle this problem and consider a simple but overlooked parameter: the number of existentially quantified variables. This natural parameter is virtually unexplored in the literature which one might find surprising given the general scarcity of FPT algorithms for QBF. Via this parameterization we then develop a novel FPT algorithm applicable to QBF instances in conjunctive normal form (CNF) of bounded clause length. We complement this by a W[1]-hardness result for QBF in CNF of unbounded clause length as well as sharper lower bounds for the bounded arity case under the (strong) exponential-time hypothesis.

The Computational Complexity of Concise Hypersphere Classification

Hypersphere classification is a classical and foundational method that can provide easy-to-process explanations for the classification of real-valued and binary data. However, obtaining an (ideally concise) explanation via hypersphere classification is much more difficult when dealing with binary data than real-valued data. In this paper, we perform the first complexity-theoretic study of the hypersphere classification problem for binary data. We use the fine-grained parameterized complexity paradigm to analyze the impact of structural properties that may be present in the input data as well as potential conciseness constraints. Our results include stronger lower bounds and new fixed-parameter algorithms for hypersphere classification of binary data, which can find an exact and concise explanation when one exists.

The Complexity of Envy-Free Graph Cutting

We consider the problem of fairly dividing a set of heterogeneous divisible resources among agents with different preferences. We focus on the setting where the resources correspond to the edges of a connected graph, every agent must be assigned a connected piece of this graph, and the fairness notion considered is the classical envy freeness. The problem is NP-complete, and we analyze its complexity with respect to two natural complexity measures: the number of agents and the number of edges in the graph. While the problem remains NP-hard even for instances with 2 agents, we provide a dichotomy characterizing the complexity of the problem when the number of agents is constant based on structural properties of the graph. For the latter case, we design a polynomial-time algorithm when the graph has a constant number of edges.

Computational Short Cuts in Infinite Domain Constraint Satisfaction

A backdoor in a finite-domain CSP instance is a set of variables where each possible instantiation moves the instance into a polynomial-time solvable class. Backdoors have found many applications in artificial intelligence and elsewhere, and the algorithmic problem of finding such backdoors has consequently been intensively studied. Sioutis and Janhunen (Proc. 42nd German Conference on AI (KI-2019)) have proposed a generalised backdoor concept suitable for infinite-domain CSP instances over binary constraints. We generalise their concept into a large class of CSPs that allow for higher-arity constraints. We show that this kind of infinite-domain backdoors have many of the positive computational properties that finite-domain backdoors have: the associated computational problems are fixed-parameter tractable whenever the underlying constraint language is finite. On the other hand, we show that infinite languages make the problems considerably harder: the general backdoor detection problem is W[2]-hard and fixed-parameter tractability is ruled out under standard complexity-theoretic assumptions. We demonstrate that backdoors may have suboptimal behaviour on binary constraints -- this is detrimental from an AI perspective where binary constraints are predominant in, for instance, spatiotemporal applications. In response to this, we introduce sidedoors as an alternative to backdoors. The fundamental computational problems for sidedoors remain fixed-parameter tractable for finite constraint language (possibly also containing non-binary relations). Moreover, the sidedoor approach has appealing computational properties that sometimes leads to faster algorithms than the backdoor approach.

Solving Infinite-Domain CSPs Using the Patchwork Property

The constraint satisfaction problem (CSP) has important applications in computer science and AI. In particular, infinite-domain CSPs have been intensively used in subareas of AI such as spatio-temporal reasoning. Since constraint satisfaction is a computationally hard problem, much work has been devoted to identifying restricted problems that are efficiently solvable. One way of doing this is to restrict the interactions of variables and constraints, and a highly successful approach is to bound the treewidth of the underlying primal graph. Bodirsky & Dalmau [J. Comput. System. Sci. 79(1), 2013] and Huang et al. [Artif. Intell. 195, 2013] proved that CSP$(\Gamma)$ can be solved in $n^{f(w)}$ time (where $n$ is the size of the instance, $w$ is the treewidth of the primal graph and $f$ is a computable function) for certain classes of constraint languages $\Gamma$. We improve this bound to $f(w) \cdot n^{O(1)}$, where the function $f$ only depends on the language $\Gamma$, for CSPs whose basic relations have the patchwork property. Hence, such problems are fixed-parameter tractable and our algorithm is asymptotically faster than the previous ones. Additionally, our approach is not restricted to binary constraints, so it is applicable to a strictly larger class of problems than that of Huang et al. However, there exist natural problems that are covered by Bodirsky & Dalmau's algorithm but not by ours, and we begin investigating ways of generalising our results to larger families of languages. We also analyse our algorithm with respect to its running time and show that it is optimal (under the Exponential Time Hypothesis) for certain languages such as Allen's Interval Algebra.

Clique-Width and Directed Width Measures for Answer-Set Programming

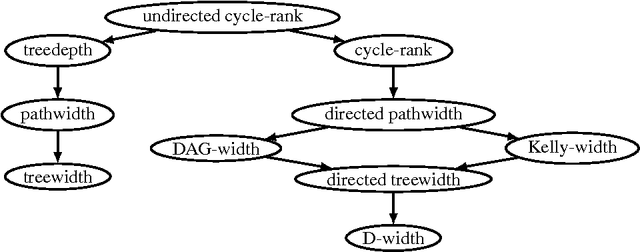
Disjunctive Answer Set Programming (ASP) is a powerful declarative programming paradigm whose main decision problems are located on the second level of the polynomial hierarchy. Identifying tractable fragments and developing efficient algorithms for such fragments are thus important objectives in order to complement the sophisticated ASP systems available to date. Hard problems can become tractable if some problem parameter is bounded by a fixed constant; such problems are then called fixed-parameter tractable (FPT). While several FPT results for ASP exist, parameters that relate to directed or signed graphs representing the program at hand have been neglected so far. In this paper, we first give some negative observations showing that directed width measures on the dependency graph of a program do not lead to FPT results. We then consider the graph parameter of signed clique-width and present a novel dynamic programming algorithm that is FPT w.r.t. this parameter. Clique-width is more general than the well-known treewidth, and, to the best of our knowledge, ours is the first FPT algorithm for bounded clique-width for reasoning problems beyond SAT.

Backdoors into Heterogeneous Classes of SAT and CSP

In this paper we extend the classical notion of strong and weak backdoor sets for SAT and CSP by allowing that different instantiations of the backdoor variables result in instances that belong to different base classes; the union of the base classes forms a heterogeneous base class. Backdoor sets to heterogeneous base classes can be much smaller than backdoor sets to homogeneous ones, hence they are much more desirable but possibly harder to find. We draw a detailed complexity landscape for the problem of detecting strong and weak backdoor sets into heterogeneous base classes for SAT and CSP.

The Complexity of Repairing, Adjusting, and Aggregating of Extensions in Abstract Argumentation

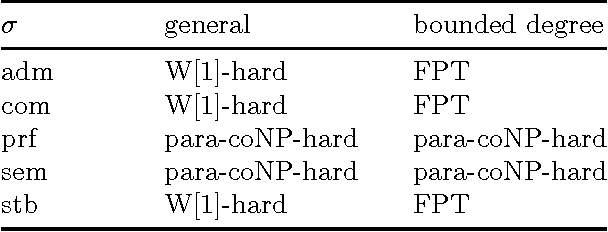
We study the computational complexity of problems that arise in abstract argumentation in the context of dynamic argumentation, minimal change, and aggregation. In particular, we consider the following problems where always an argumentation framework F and a small positive integer k are given. - The Repair problem asks whether a given set of arguments can be modified into an extension by at most k elementary changes (i.e., the extension is of distance k from the given set). - The Adjust problem asks whether a given extension can be modified by at most k elementary changes into an extension that contains a specified argument. - The Center problem asks whether, given two extensions of distance k, whether there is a "center" extension that is a distance at most (k-1) from both given extensions. We study these problems in the framework of parameterized complexity, and take the distance k as the parameter. Our results covers several different semantics, including admissible, complete, preferred, semi-stable and stable semantics.

Parameterized Complexity Results for Exact Bayesian Network Structure Learning

Bayesian network structure learning is the notoriously difficult problem of discovering a Bayesian network that optimally represents a given set of training data. In this paper we study the computational worst-case complexity of exact Bayesian network structure learning under graph theoretic restrictions on the (directed) super-structure. The super-structure is an undirected graph that contains as subgraphs the skeletons of solution networks. We introduce the directed super-structure as a natural generalization of its undirected counterpart. Our results apply to several variants of score-based Bayesian network structure learning where the score of a network decomposes into local scores of its nodes. Results: We show that exact Bayesian network structure learning can be carried out in non-uniform polynomial time if the super-structure has bounded treewidth, and in linear time if in addition the super-structure has bounded maximum degree. Furthermore, we show that if the directed super-structure is acyclic, then exact Bayesian network structure learning can be carried out in quadratic time. We complement these positive results with a number of hardness results. We show that both restrictions (treewidth and degree) are essential and cannot be dropped without loosing uniform polynomial time tractability (subject to a complexity-theoretic assumption). Similarly, exact Bayesian network structure learning remains NP-hard for "almost acyclic" directed super-structures. Furthermore, we show that the restrictions remain essential if we do not search for a globally optimal network but aim to improve a given network by means of at most k arc additions, arc deletions, or arc reversals (k-neighborhood local search).