The Power of Arc Consistency for CSPs Defined by Partially-Ordered Forbidden Patterns

Characterising tractable fragments of the constraint satisfaction problem (CSP) is an important challenge in theoretical computer science and artificial intelligence. Forbidding patterns (generic sub-instances) provides a means of defining CSP fragments which are neither exclusively language-based nor exclusively structure-based. It is known that the class of binary CSP instances in which the broken-triangle pattern (BTP) does not occur, a class which includes all tree-structured instances, are decided by arc consistency (AC), a ubiquitous reduction operation in constraint solvers. We provide a characterisation of simple partially-ordered forbidden patterns which have this AC-solvability property. It turns out that BTP is just one of five such AC-solvable patterns. The four other patterns allow us to exhibit new tractable classes.

Backdoors into Heterogeneous Classes of SAT and CSP

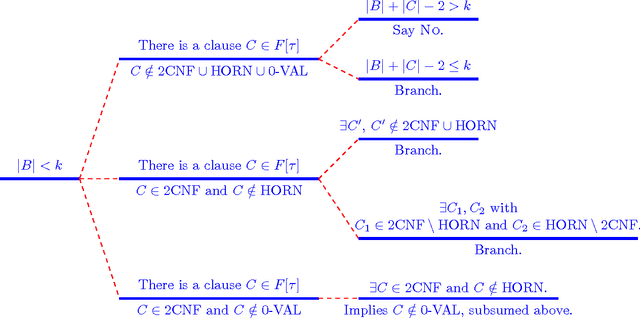
In this paper we extend the classical notion of strong and weak backdoor sets for SAT and CSP by allowing that different instantiations of the backdoor variables result in instances that belong to different base classes; the union of the base classes forms a heterogeneous base class. Backdoor sets to heterogeneous base classes can be much smaller than backdoor sets to homogeneous ones, hence they are much more desirable but possibly harder to find. We draw a detailed complexity landscape for the problem of detecting strong and weak backdoor sets into heterogeneous base classes for SAT and CSP.

Tractable Triangles and Cross-Free Convexity in Discrete Optimisation

The minimisation problem of a sum of unary and pairwise functions of discrete variables is a general NP-hard problem with wide applications such as computing MAP configurations in Markov Random Fields (MRF), minimising Gibbs energy, or solving binary Valued Constraint Satisfaction Problems (VCSPs). We study the computational complexity of classes of discrete optimisation problems given by allowing only certain types of costs in every triangle of variable-value assignments to three distinct variables. We show that for several computational problems, the only non- trivial tractable classes are the well known maximum matching problem and the recently discovered joint-winner property. Our results, apart from giving complete classifications in the studied cases, provide guidance in the search for hybrid tractable classes; that is, classes of problems that are not captured by restrictions on the functions (such as submodularity) or the structure of the problem graph (such as bounded treewidth). Furthermore, we introduce a class of problems with convex cardinality functions on cross-free sets of assignments. We prove that while imposing only one of the two conditions renders the problem NP-hard, the conjunction of the two gives rise to a novel tractable class satisfying the cross-free convexity property, which generalises the joint-winner property to problems of unbounded arity.

Tractable Combinations of Global Constraints

We study the complexity of constraint satisfaction problems involving global constraints, i.e., special-purpose constraints provided by a solver and represented implicitly by a parametrised algorithm. Such constraints are widely used; indeed, they are one of the key reasons for the success of constraint programming in solving real-world problems. Previous work has focused on the development of efficient propagators for individual constraints. In this paper, we identify a new tractable class of constraint problems involving global constraints of unbounded arity. To do so, we combine structural restrictions with the observation that some important types of global constraint do not distinguish between large classes of equivalent solutions.