Axiomatic Characterisations of Sample-based Explainers

Explaining decisions of black-box classifiers is both important and computationally challenging. In this paper, we scrutinize explainers that generate feature-based explanations from samples or datasets. We start by presenting a set of desirable properties that explainers would ideally satisfy, delve into their relationships, and highlight incompatibilities of some of them. We identify the entire family of explainers that satisfy two key properties which are compatible with all the others. Its instances provide sufficient reasons, called weak abductive explanations.We then unravel its various subfamilies that satisfy subsets of compatible properties. Indeed, we fully characterize all the explainers that satisfy any subset of compatible properties. In particular, we introduce the first (broad family of) explainers that guarantee the existence of explanations and their global consistency.We discuss some of its instances including the irrefutable explainer and the surrogate explainer whose explanations can be found in polynomial time.

Backward explanations via redefinition of predicates

History eXplanation based on Predicates (HXP), studies the behavior of a Reinforcement Learning (RL) agent in a sequence of agent's interactions with the environment (a history), through the prism of an arbitrary predicate. To this end, an action importance score is computed for each action in the history. The explanation consists in displaying the most important actions to the user. As the calculation of an action's importance is #W[1]-hard, it is necessary for long histories to approximate the scores, at the expense of their quality. We therefore propose a new HXP method, called Backward-HXP, to provide explanations for these histories without having to approximate scores. Experiments show the ability of B-HXP to summarise long histories.

Homomorphisms and Embeddings of STRIPS Planning Models

Determining whether two STRIPS planning instances are isomorphic is the simplest form of comparison between planning instances. It is also a particular case of the problem concerned with finding an isomorphism between a planning instance $P$ and a sub-instance of another instance $P_0$ . One application of such a mapping is to efficiently produce a compiled form containing all solutions to P from a compiled form containing all solutions to $P_0$. We also introduce the notion of embedding from an instance $P$ to another instance $P_0$, which allows us to deduce that $P_0$ has no solution-plan if $P$ is unsolvable. In this paper, we study the complexity of these problems. We show that the first is GI-complete, and can thus be solved, in theory, in quasi-polynomial time. While we prove the remaining problems to be NP-complete, we propose an algorithm to build an isomorphism, when possible. We report extensive experimental trials on benchmark problems which demonstrate conclusively that applying constraint propagation in preprocessing can greatly improve the efficiency of a SAT solver.

On Computing Probabilistic Abductive Explanations

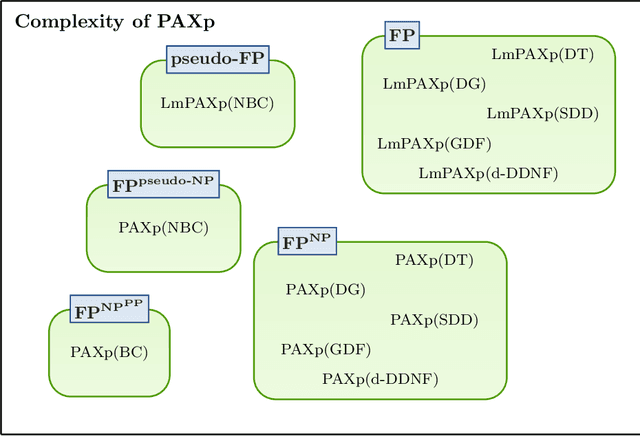
The most widely studied explainable AI (XAI) approaches are unsound. This is the case with well-known model-agnostic explanation approaches, and it is also the case with approaches based on saliency maps. One solution is to consider intrinsic interpretability, which does not exhibit the drawback of unsoundness. Unfortunately, intrinsic interpretability can display unwieldy explanation redundancy. Formal explainability represents the alternative to these non-rigorous approaches, with one example being PI-explanations. Unfortunately, PI-explanations also exhibit important drawbacks, the most visible of which is arguably their size. Recently, it has been observed that the (absolute) rigor of PI-explanations can be traded off for a smaller explanation size, by computing the so-called relevant sets. Given some positive {\delta}, a set S of features is {\delta}-relevant if, when the features in S are fixed, the probability of getting the target class exceeds {\delta}. However, even for very simple classifiers, the complexity of computing relevant sets of features is prohibitive, with the decision problem being NPPP-complete for circuit-based classifiers. In contrast with earlier negative results, this paper investigates practical approaches for computing relevant sets for a number of widely used classifiers that include Decision Trees (DTs), Naive Bayes Classifiers (NBCs), and several families of classifiers obtained from propositional languages. Moreover, the paper shows that, in practice, and for these families of classifiers, relevant sets are easy to compute. Furthermore, the experiments confirm that succinct sets of relevant features can be obtained for the families of classifiers considered.

Feature Necessity & Relevancy in ML Classifier Explanations

Given a machine learning (ML) model and a prediction, explanations can be defined as sets of features which are sufficient for the prediction. In some applications, and besides asking for an explanation, it is also critical to understand whether sensitive features can occur in some explanation, or whether a non-interesting feature must occur in all explanations. This paper starts by relating such queries respectively with the problems of relevancy and necessity in logic-based abduction. The paper then proves membership and hardness results for several families of ML classifiers. Afterwards the paper proposes concrete algorithms for two classes of classifiers. The experimental results confirm the scalability of the proposed algorithms.

Provably Precise, Succinct and Efficient Explanations for Decision Trees

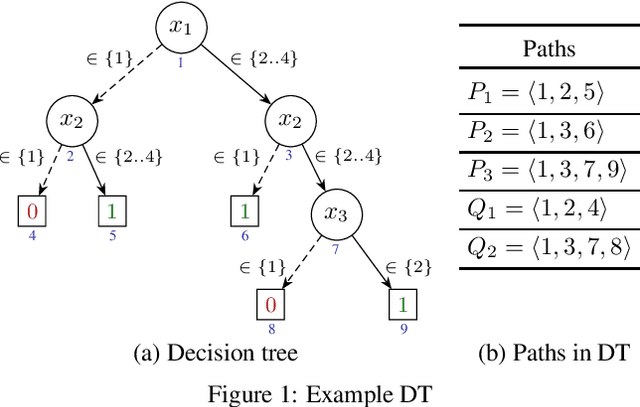
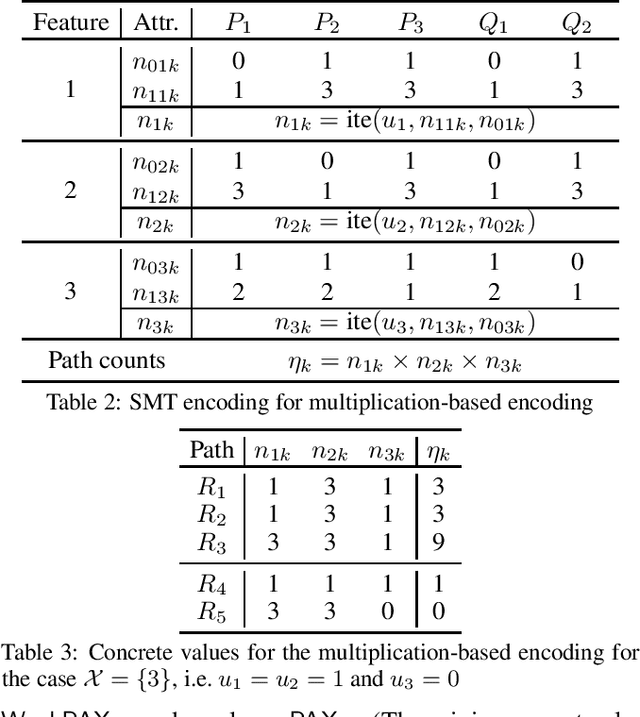
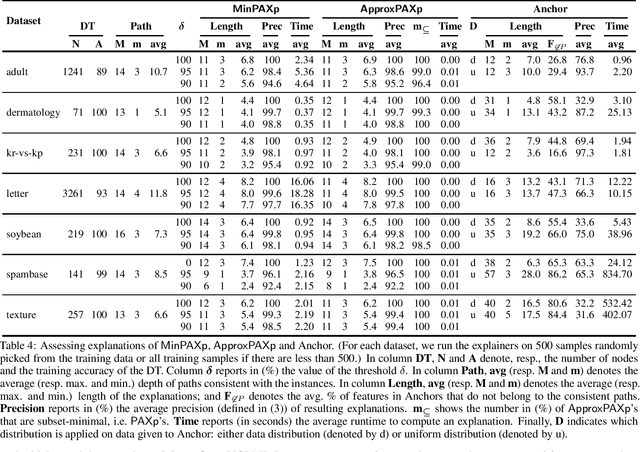
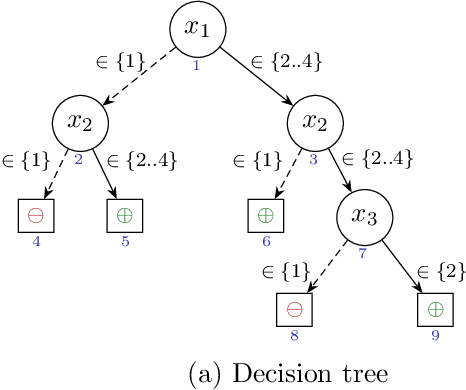
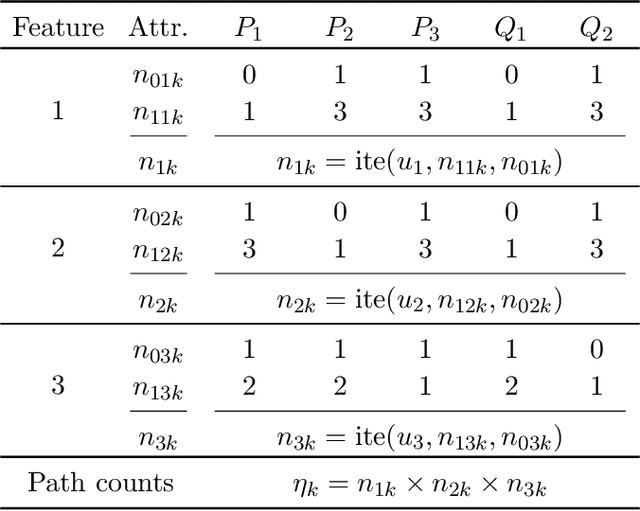
Decision trees (DTs) embody interpretable classifiers. DTs have been advocated for deployment in high-risk applications, but also for explaining other complex classifiers. Nevertheless, recent work has demonstrated that predictions in DTs ought to be explained with rigorous approaches. Although rigorous explanations can be computed in polynomial time for DTs, their size may be beyond the cognitive limits of human decision makers. This paper investigates the computation of {\delta}-relevant sets for DTs. {\delta}-relevant sets denote explanations that are succinct and provably precise. These sets represent generalizations of rigorous explanations, which are precise with probability one, and so they enable trading off explanation size for precision. The paper proposes two logic encodings for computing smallest {\delta}-relevant sets for DTs. The paper further devises a polynomial-time algorithm for computing {\delta}-relevant sets which are not guaranteed to be subset-minimal, but for which the experiments show to be most often subset-minimal in practice. The experimental results also demonstrate the practical efficiency of computing smallest {\delta}-relevant sets.

Efficient Explanations for Knowledge Compilation Languages

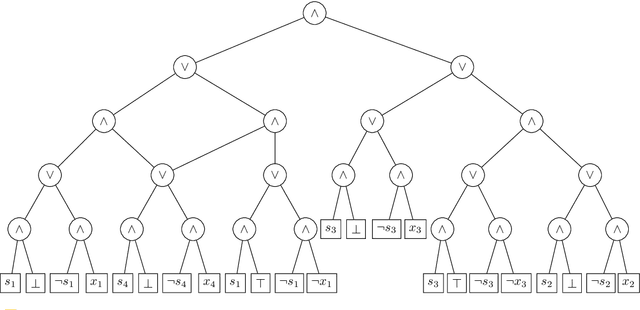
Knowledge compilation (KC) languages find a growing number of practical uses, including in Constraint Programming (CP) and in Machine Learning (ML). In most applications, one natural question is how to explain the decisions made by models represented by a KC language. This paper shows that for many of the best known KC languages, well-known classes of explanations can be computed in polynomial time. These classes include deterministic decomposable negation normal form (d-DNNF), and so any KC language that is strictly less succinct than d-DNNF. Furthermore, the paper also investigates the conditions under which polynomial time computation of explanations can be extended to KC languages more succinct than d-DNNF.

Efficient Explanations With Relevant Sets

Recent work proposed $\delta$-relevant inputs (or sets) as a probabilistic explanation for the predictions made by a classifier on a given input. $\delta$-relevant sets are significant because they serve to relate (model-agnostic) Anchors with (model-accurate) PI- explanations, among other explanation approaches. Unfortunately, the computation of smallest size $\delta$-relevant sets is complete for ${NP}^{PP}$, rendering their computation largely infeasible in practice. This paper investigates solutions for tackling the practical limitations of $\delta$-relevant sets. First, the paper alternatively considers the computation of subset-minimal sets. Second, the paper studies concrete families of classifiers, including decision trees among others. For these cases, the paper shows that the computation of subset-minimal $\delta$-relevant sets is in NP, and can be solved with a polynomial number of calls to an NP oracle. The experimental evaluation compares the proposed approach with heuristic explainers for the concrete case of the classifiers studied in the paper, and confirms the advantage of the proposed solution over the state of the art.

Explaining Naive Bayes and Other Linear Classifiers with Polynomial Time and Delay

Recent work proposed the computation of so-called PI-explanations of Naive Bayes Classifiers (NBCs). PI-explanations are subset-minimal sets of feature-value pairs that are sufficient for the prediction, and have been computed with state-of-the-art exact algorithms that are worst-case exponential in time and space. In contrast, we show that the computation of one PI-explanation for an NBC can be achieved in log-linear time, and that the same result also applies to the more general class of linear classifiers. Furthermore, we show that the enumeration of PI-explanations can be obtained with polynomial delay. Experimental results demonstrate the performance gains of the new algorithms when compared with earlier work. The experimental results also investigate ways to measure the quality of heuristic explanations

Strengthening neighbourhood substitution

Domain reduction is an essential tool for solving the constraint satisfaction problem (CSP). In the binary CSP, neighbourhood substitution consists in eliminating a value if there exists another value which can be substituted for it in each constraint. We show that the notion of neighbourhood substitution can be strengthened in two distinct ways without increasing time complexity. We also show the theoretical result that, unlike neighbourhood substitution, finding an optimal sequence of these new operations is NP-hard.