Distance-Restricted Explanations: Theoretical Underpinnings & Efficient Implementation

The uses of machine learning (ML) have snowballed in recent years. In many cases, ML models are highly complex, and their operation is beyond the understanding of human decision-makers. Nevertheless, some uses of ML models involve high-stakes and safety-critical applications. Explainable artificial intelligence (XAI) aims to help human decision-makers in understanding the operation of such complex ML models, thus eliciting trust in their operation. Unfortunately, the majority of past XAI work is based on informal approaches, that offer no guarantees of rigor. Unsurprisingly, there exists comprehensive experimental and theoretical evidence confirming that informal methods of XAI can provide human-decision makers with erroneous information. Logic-based XAI represents a rigorous approach to explainability; it is model-based and offers the strongest guarantees of rigor of computed explanations. However, a well-known drawback of logic-based XAI is the complexity of logic reasoning, especially for highly complex ML models. Recent work proposed distance-restricted explanations, i.e. explanations that are rigorous provided the distance to a given input is small enough. Distance-restricted explainability is tightly related with adversarial robustness, and it has been shown to scale for moderately complex ML models, but the number of inputs still represents a key limiting factor. This paper investigates novel algorithms for scaling up the performance of logic-based explainers when computing and enumerating ML model explanations with a large number of inputs.

Locally-Minimal Probabilistic Explanations

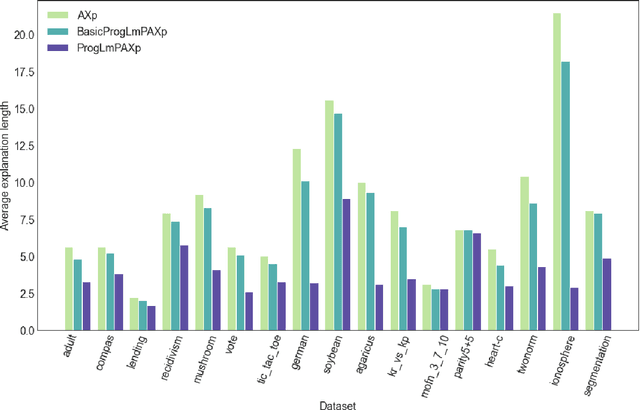
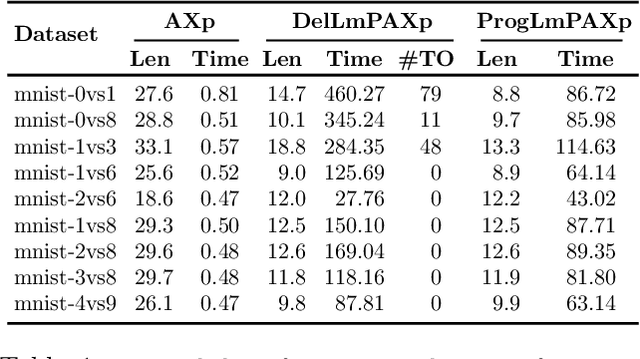
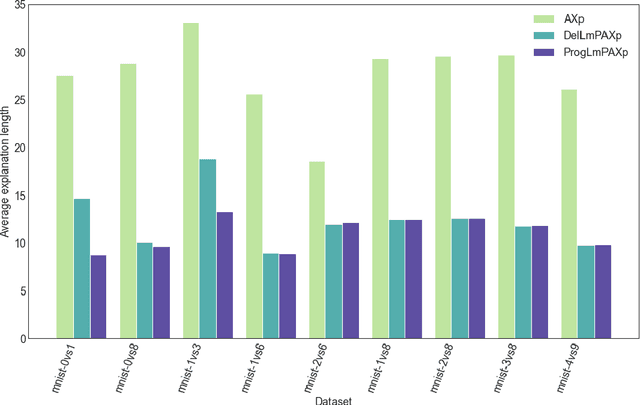
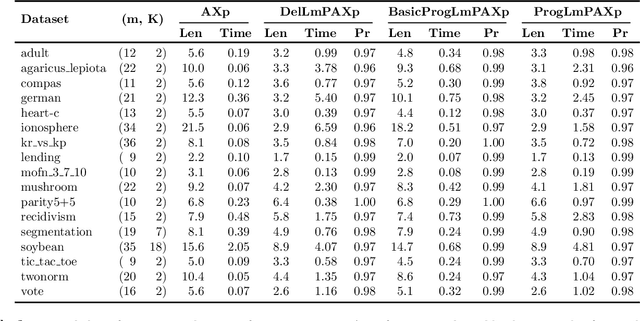
Formal abductive explanations offer crucial guarantees of rigor and so are of interest in high-stakes uses of machine learning (ML). One drawback of abductive explanations is explanation size, justified by the cognitive limits of human decision-makers. Probabilistic abductive explanations (PAXps) address this limitation, but their theoretical and practical complexity makes their exact computation most often unrealistic. This paper proposes novel efficient algorithms for the computation of locally-minimal PXAps, which offer high-quality approximations of PXAps in practice. The experimental results demonstrate the practical efficiency of the proposed algorithms.

The Pros and Cons of Adversarial Robustness

Robustness is widely regarded as a fundamental problem in the analysis of machine learning (ML) models. Most often robustness equates with deciding the non-existence of adversarial examples, where adversarial examples denote situations where small changes on some inputs cause a change in the prediction. The perceived importance of ML model robustness explains the continued progress observed for most of the last decade. Whereas robustness is often assessed locally, i.e. given some target point in feature space, robustness can also be defined globally, i.e. where any point in feature space can be considered. The importance of ML model robustness is illustrated for example by the existence of competitions evaluating the progress of robustness tools, namely in the case of neural networks (NNs) but also by efforts towards robustness certification. More recently, robustness tools have also been used for computing rigorous explanations of ML models. In contrast with the observed successes of robustness, this paper uncovers some limitations with existing definitions of robustness, both global and local, but also with efforts towards robustness certification. The paper also investigates uses of adversarial examples besides those related with robustness.

Axiomatic Aggregations of Abductive Explanations

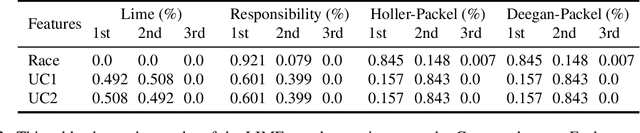
The recent criticisms of the robustness of post hoc model approximation explanation methods (like LIME and SHAP) have led to the rise of model-precise abductive explanations. For each data point, abductive explanations provide a minimal subset of features that are sufficient to generate the outcome. While theoretically sound and rigorous, abductive explanations suffer from a major issue -- there can be several valid abductive explanations for the same data point. In such cases, providing a single abductive explanation can be insufficient; on the other hand, providing all valid abductive explanations can be incomprehensible due to their size. In this work, we solve this issue by aggregating the many possible abductive explanations into feature importance scores. We propose three aggregation methods: two based on power indices from cooperative game theory and a third based on a well-known measure of causal strength. We characterize these three methods axiomatically, showing that each of them uniquely satisfies a set of desirable properties. We also evaluate them on multiple datasets and show that these explanations are robust to the attacks that fool SHAP and LIME.

Delivering Inflated Explanations

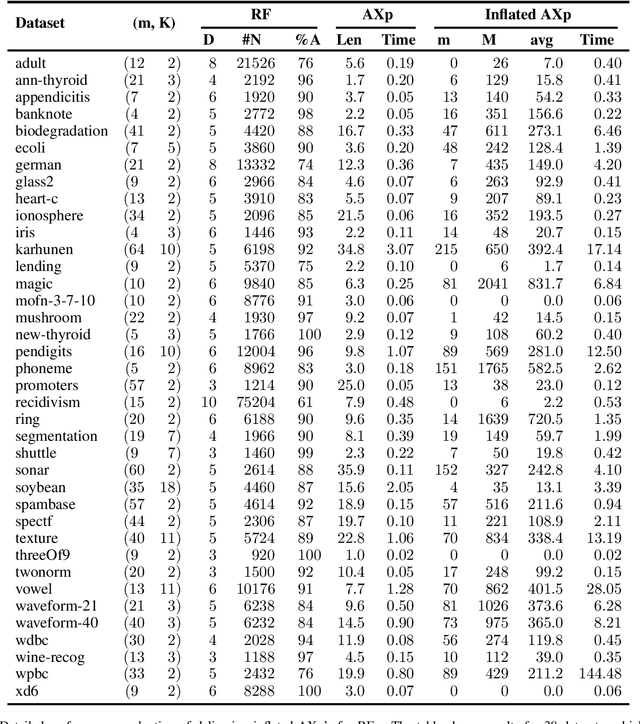
In the quest for Explainable Artificial Intelligence (XAI) one of the questions that frequently arises given a decision made by an AI system is, ``why was the decision made in this way?'' Formal approaches to explainability build a formal model of the AI system and use this to reason about the properties of the system. Given a set of feature values for an instance to be explained, and a resulting decision, a formal abductive explanation is a set of features, such that if they take the given value will always lead to the same decision. This explanation is useful, it shows that only some features were used in making the final decision. But it is narrow, it only shows that if the selected features take their given values the decision is unchanged. It's possible that some features may change values and still lead to the same decision. In this paper we formally define inflated explanations which is a set of features, and for each feature of set of values (always including the value of the instance being explained), such that the decision will remain unchanged. Inflated explanations are more informative than abductive explanations since e.g they allow us to see if the exact value of a feature is important, or it could be any nearby value. Overall they allow us to better understand the role of each feature in the decision. We show that we can compute inflated explanations for not that much greater cost than abductive explanations, and that we can extend duality results for abductive explanations also to inflated explanations.

On Computing Probabilistic Abductive Explanations

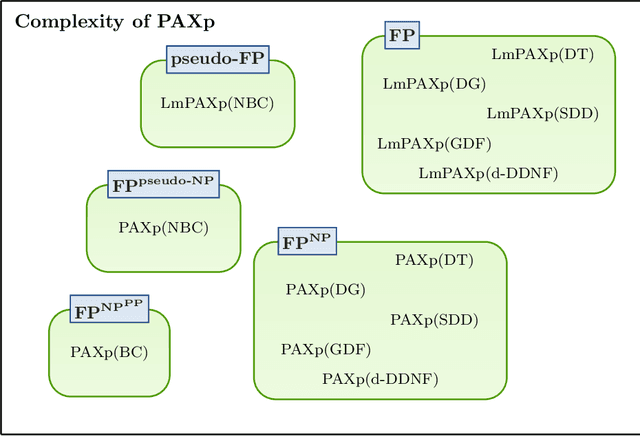
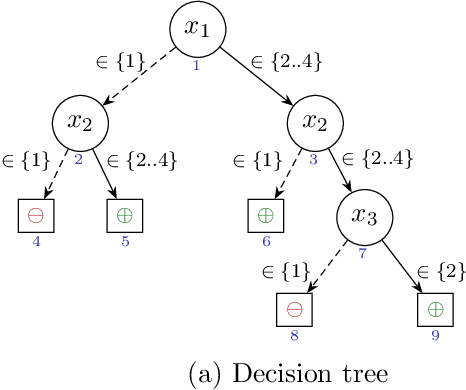
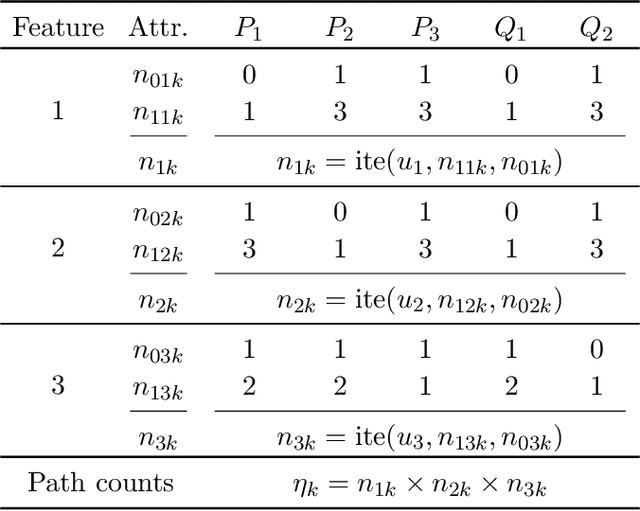
The most widely studied explainable AI (XAI) approaches are unsound. This is the case with well-known model-agnostic explanation approaches, and it is also the case with approaches based on saliency maps. One solution is to consider intrinsic interpretability, which does not exhibit the drawback of unsoundness. Unfortunately, intrinsic interpretability can display unwieldy explanation redundancy. Formal explainability represents the alternative to these non-rigorous approaches, with one example being PI-explanations. Unfortunately, PI-explanations also exhibit important drawbacks, the most visible of which is arguably their size. Recently, it has been observed that the (absolute) rigor of PI-explanations can be traded off for a smaller explanation size, by computing the so-called relevant sets. Given some positive {\delta}, a set S of features is {\delta}-relevant if, when the features in S are fixed, the probability of getting the target class exceeds {\delta}. However, even for very simple classifiers, the complexity of computing relevant sets of features is prohibitive, with the decision problem being NPPP-complete for circuit-based classifiers. In contrast with earlier negative results, this paper investigates practical approaches for computing relevant sets for a number of widely used classifiers that include Decision Trees (DTs), Naive Bayes Classifiers (NBCs), and several families of classifiers obtained from propositional languages. Moreover, the paper shows that, in practice, and for these families of classifiers, relevant sets are easy to compute. Furthermore, the experiments confirm that succinct sets of relevant features can be obtained for the families of classifiers considered.

On Computing Relevant Features for Explaining NBCs

Despite the progress observed with model-agnostic explainable AI (XAI), it is the case that model-agnostic XAI can produce incorrect explanations. One alternative are the so-called formal approaches to XAI, that include PI-explanations. Unfortunately, PI-explanations also exhibit important drawbacks, the most visible of which is arguably their size. The computation of relevant features serves to trade off probabilistic precision for the number of features in an explanation. However, even for very simple classifiers, the complexity of computing sets of relevant features is prohibitive. This paper investigates the computation of relevant sets for Naive Bayes Classifiers (NBCs), and shows that, in practice, these are easy to compute. Furthermore, the experiments confirm that succinct sets of relevant features can be obtained with NBCs.

On Tackling Explanation Redundancy in Decision Trees

Decision trees (DTs) epitomize the ideal of interpretability of machine learning (ML) models. The interpretability of decision trees motivates explainability approaches by so-called intrinsic interpretability, and it is at the core of recent proposals for applying interpretable ML models in high-risk applications. The belief in DT interpretability is justified by the fact that explanations for DT predictions are generally expected to be succinct. Indeed, in the case of DTs, explanations correspond to DT paths. Since decision trees are ideally shallow, and so paths contain far fewer features than the total number of features, explanations in DTs are expected to be succinct, and hence interpretable. This paper offers both theoretical and experimental arguments demonstrating that, as long as interpretability of decision trees equates with succinctness of explanations, then decision trees ought not be deemed interpretable. The paper introduces logically rigorous path explanations and path explanation redundancy, and proves that there exist functions for which decision trees must exhibit paths with arbitrarily large explanation redundancy. The paper also proves that only a very restricted class of functions can be represented with DTs that exhibit no explanation redundancy. In addition, the paper includes experimental results substantiating that path explanation redundancy is observed ubiquitously in decision trees, including those obtained using different tree learning algorithms, but also in a wide range of publicly available decision trees. The paper also proposes polynomial-time algorithms for eliminating path explanation redundancy, which in practice require negligible time to compute. Thus, these algorithms serve to indirectly attain irreducible, and so succinct, explanations for decision trees.

Provably Precise, Succinct and Efficient Explanations for Decision Trees

Decision trees (DTs) embody interpretable classifiers. DTs have been advocated for deployment in high-risk applications, but also for explaining other complex classifiers. Nevertheless, recent work has demonstrated that predictions in DTs ought to be explained with rigorous approaches. Although rigorous explanations can be computed in polynomial time for DTs, their size may be beyond the cognitive limits of human decision makers. This paper investigates the computation of {\delta}-relevant sets for DTs. {\delta}-relevant sets denote explanations that are succinct and provably precise. These sets represent generalizations of rigorous explanations, which are precise with probability one, and so they enable trading off explanation size for precision. The paper proposes two logic encodings for computing smallest {\delta}-relevant sets for DTs. The paper further devises a polynomial-time algorithm for computing {\delta}-relevant sets which are not guaranteed to be subset-minimal, but for which the experiments show to be most often subset-minimal in practice. The experimental results also demonstrate the practical efficiency of computing smallest {\delta}-relevant sets.

Efficient Explanations for Knowledge Compilation Languages

Knowledge compilation (KC) languages find a growing number of practical uses, including in Constraint Programming (CP) and in Machine Learning (ML). In most applications, one natural question is how to explain the decisions made by models represented by a KC language. This paper shows that for many of the best known KC languages, well-known classes of explanations can be computed in polynomial time. These classes include deterministic decomposable negation normal form (d-DNNF), and so any KC language that is strictly less succinct than d-DNNF. Furthermore, the paper also investigates the conditions under which polynomial time computation of explanations can be extended to KC languages more succinct than d-DNNF.