Dynamic Replanning for Improved Public Transport Routing

Delays in public transport are common, often impacting users through prolonged travel times and missed transfers. Existing solutions for handling delays remain limited; backup plans based on historical data miss opportunities for earlier arrivals, while snapshot planning accounts for current delays but not future ones. With the growing availability of live delay data, users can adjust their journeys in real-time. However, the literature lacks a framework that fully exploits this advantage for system-scale dynamic replanning. To address this, we formalise the dynamic replanning problem in public transport routing and propose two solutions: a "pull" approach, where users manually request replanning, and a novel "push" approach, where the server proactively monitors and adjusts journeys. Our experiments show that the push approach outperforms the pull approach, achieving significant speedups. The results also reveal substantial arrival time savings enabled by dynamic replanning.

Temporal Planning via Interval Logic Satisfiability for Autonomous Systems

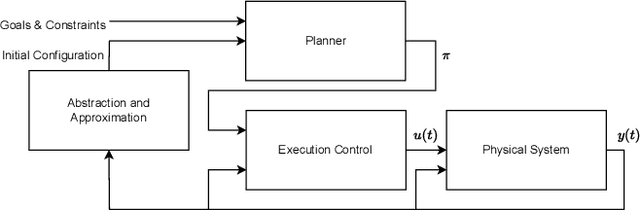
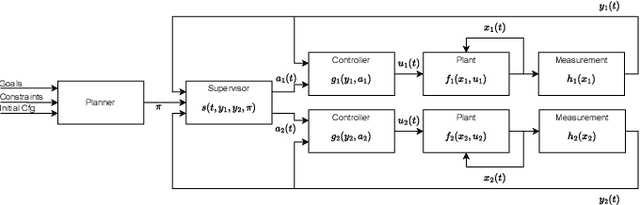
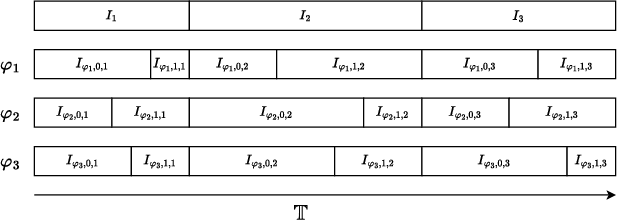
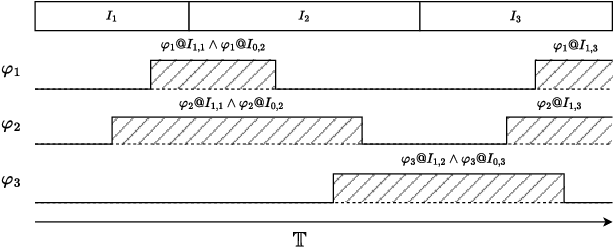
Many automated planning methods and formulations rely on suitably designed abstractions or simplifications of the constrained dynamics associated with agents to attain computational scalability. We consider formulations of temporal planning where intervals are associated with both action and fluent atoms, and relations between these are given as sentences in Allen's Interval Logic. We propose a notion of planning graphs that can account for complex concurrency relations between actions and fluents as a Constraint Programming (CP) model. We test an implementation of our algorithm on a state-of-the-art framework for CP and compare it with PDDL 2.1 planners that capture plans requiring complex concurrent interactions between agents. We demonstrate our algorithm outperforms existing PDDL 2.1 planners in the case studies. Still, scalability remains challenging when plans must comply with intricate concurrent interactions and the sequencing of actions.

Delivering Inflated Explanations

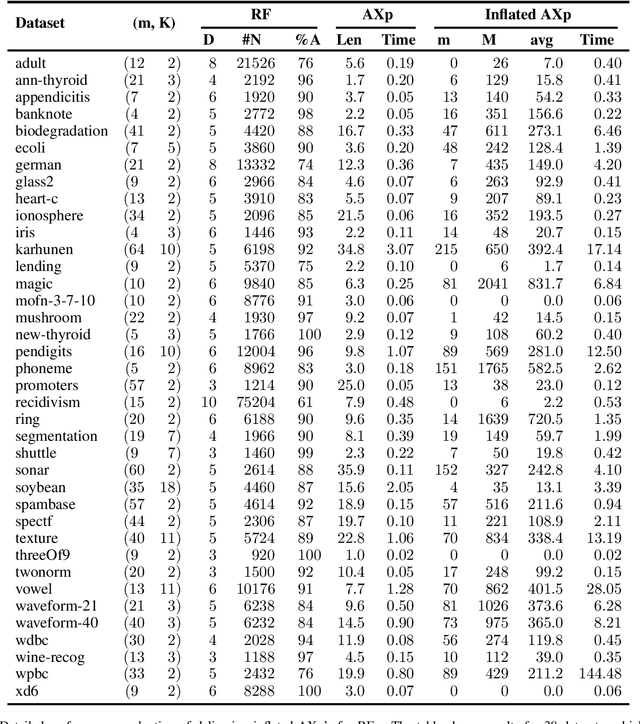
In the quest for Explainable Artificial Intelligence (XAI) one of the questions that frequently arises given a decision made by an AI system is, ``why was the decision made in this way?'' Formal approaches to explainability build a formal model of the AI system and use this to reason about the properties of the system. Given a set of feature values for an instance to be explained, and a resulting decision, a formal abductive explanation is a set of features, such that if they take the given value will always lead to the same decision. This explanation is useful, it shows that only some features were used in making the final decision. But it is narrow, it only shows that if the selected features take their given values the decision is unchanged. It's possible that some features may change values and still lead to the same decision. In this paper we formally define inflated explanations which is a set of features, and for each feature of set of values (always including the value of the instance being explained), such that the decision will remain unchanged. Inflated explanations are more informative than abductive explanations since e.g they allow us to see if the exact value of a feature is important, or it could be any nearby value. Overall they allow us to better understand the role of each feature in the decision. We show that we can compute inflated explanations for not that much greater cost than abductive explanations, and that we can extend duality results for abductive explanations also to inflated explanations.

Comparison and Evaluation of Methods for a Predict+Optimize Problem in Renewable Energy

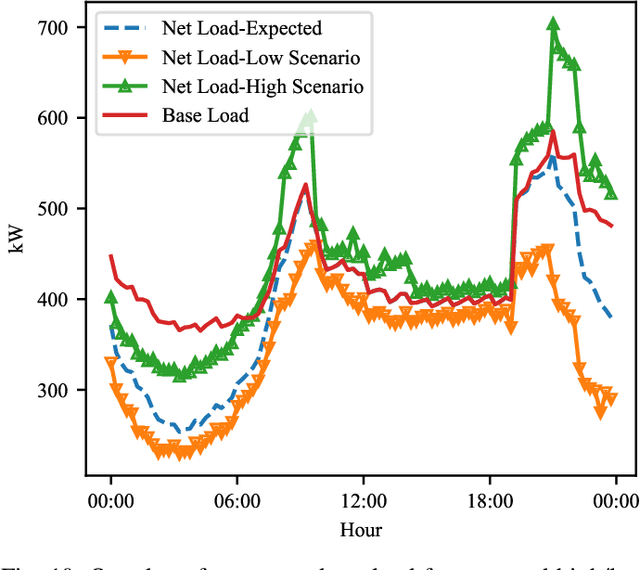
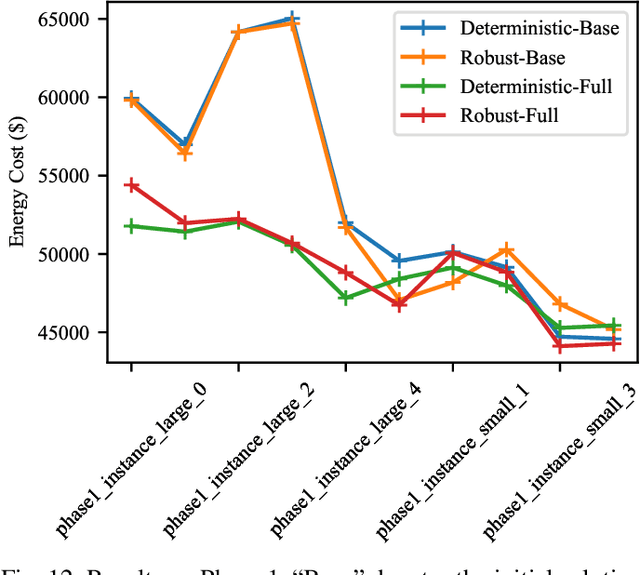
Algorithms that involve both forecasting and optimization are at the core of solutions to many difficult real-world problems, such as in supply chains (inventory optimization), traffic, and in the transition towards carbon-free energy generation in battery/load/production scheduling in sustainable energy systems. Typically, in these scenarios we want to solve an optimization problem that depends on unknown future values, which therefore need to be forecast. As both forecasting and optimization are difficult problems in their own right, relatively few research has been done in this area. This paper presents the findings of the ``IEEE-CIS Technical Challenge on Predict+Optimize for Renewable Energy Scheduling," held in 2021. We present a comparison and evaluation of the seven highest-ranked solutions in the competition, to provide researchers with a benchmark problem and to establish the state of the art for this benchmark, with the aim to foster and facilitate research in this area. The competition used data from the Monash Microgrid, as well as weather data and energy market data. It then focused on two main challenges: forecasting renewable energy production and demand, and obtaining an optimal schedule for the activities (lectures) and on-site batteries that lead to the lowest cost of energy. The most accurate forecasts were obtained by gradient-boosted tree and random forest models, and optimization was mostly performed using mixed integer linear and quadratic programming. The winning method predicted different scenarios and optimized over all scenarios jointly using a sample average approximation method.

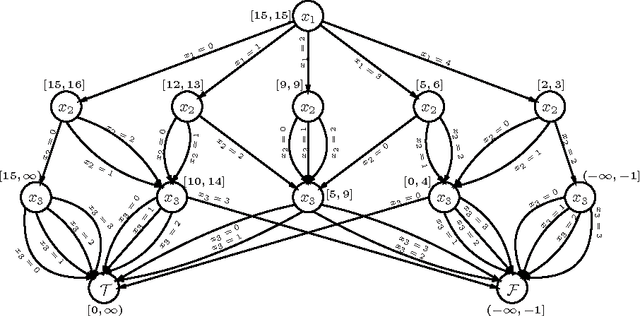
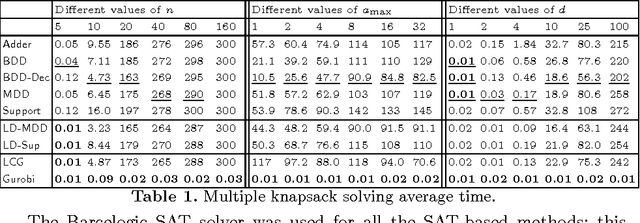
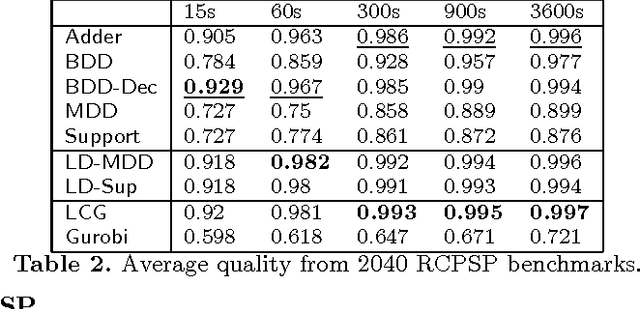
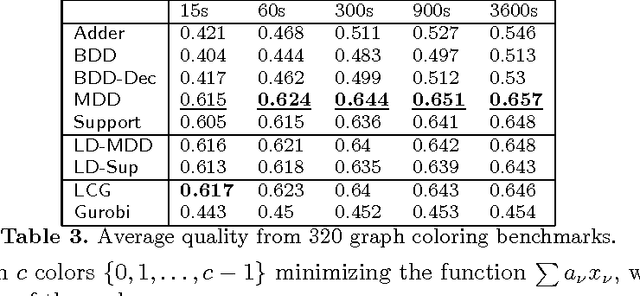
Encoding Linear Constraints into SAT

Linear integer constraints are one of the most important constraints in combinatorial problems since they are commonly found in many practical applications. Typically, encodings to Boolean satisfiability (SAT) format of conjunctive normal form perform poorly in problems with these constraints in comparison with SAT modulo theories (SMT), lazy clause generation (LCG) or mixed integer programming (MIP) solvers. In this paper we explore and categorize SAT encodings for linear integer constraints. We define new SAT encodings based on multi-valued decision diagrams, and sorting networks. We compare different SAT encodings of linear constraints and demonstrate where one may be preferable to another. We also compare SAT encodings against other solving methods and show they can be better than linear integer (MIP) solvers and sometimes better than LCG or SMT solvers on appropriate problems. Combining the new encoding with lazy decomposition, which during runtime only encodes constraints that are important to the solving process that occurs, gives the best option for many highly combinatorial problems involving linear constraints.

Projected Model Counting

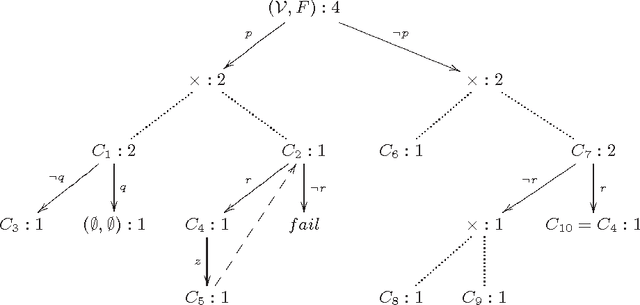
Model counting is the task of computing the number of assignments to variables V that satisfy a given propositional theory F. Model counting is an essential tool in probabilistic reasoning. In this paper, we introduce the problem of model counting projected on a subset P of original variables that we call 'priority' variables. The task is to compute the number of assignments to P such that there exists an extension to 'non-priority' variables V\P that satisfies F. Projected model counting arises when some parts of the model are irrelevant to the counts, in particular when we require additional variables to model the problem we are counting in SAT. We discuss three different approaches to projected model counting (two of which are novel), and compare their performance on different benchmark problems. To appear in 18th International Conference on Theory and Applications of Satisfiability Testing, September 24-27, 2015, Austin, Texas, USA

Stable Model Counting and Its Application in Probabilistic Logic Programming

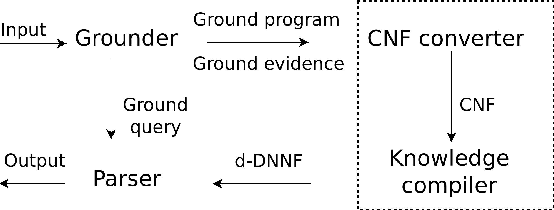
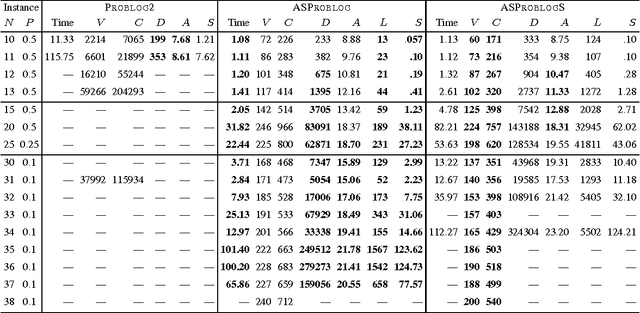
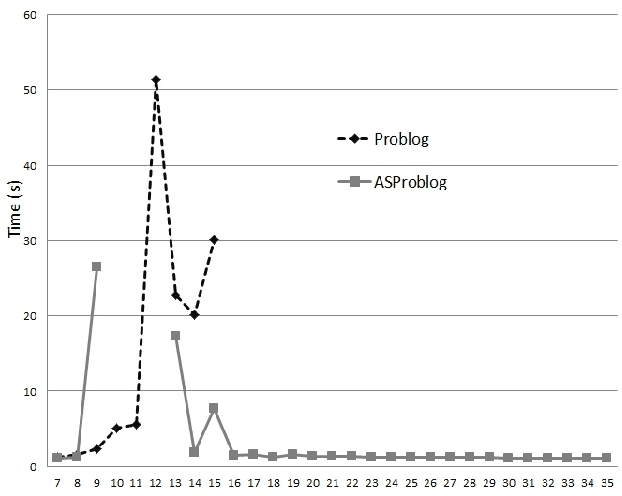
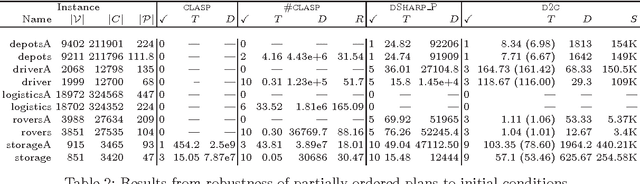
Model counting is the problem of computing the number of models that satisfy a given propositional theory. It has recently been applied to solving inference tasks in probabilistic logic programming, where the goal is to compute the probability of given queries being true provided a set of mutually independent random variables, a model (a logic program) and some evidence. The core of solving this inference task involves translating the logic program to a propositional theory and using a model counter. In this paper, we show that for some problems that involve inductive definitions like reachability in a graph, the translation of logic programs to SAT can be expensive for the purpose of solving inference tasks. For such problems, direct implementation of stable model semantics allows for more efficient solving. We present two implementation techniques, based on unfounded set detection, that extend a propositional model counter to a stable model counter. Our experiments show that for particular problems, our approach can outperform a state-of-the-art probabilistic logic programming solver by several orders of magnitude in terms of running time and space requirements, and can solve instances of significantly larger sizes on which the current solver runs out of time or memory.