Projected Model Counting

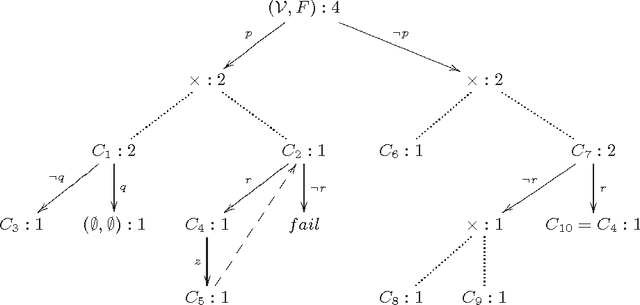
Model counting is the task of computing the number of assignments to variables V that satisfy a given propositional theory F. Model counting is an essential tool in probabilistic reasoning. In this paper, we introduce the problem of model counting projected on a subset P of original variables that we call 'priority' variables. The task is to compute the number of assignments to P such that there exists an extension to 'non-priority' variables V\P that satisfies F. Projected model counting arises when some parts of the model are irrelevant to the counts, in particular when we require additional variables to model the problem we are counting in SAT. We discuss three different approaches to projected model counting (two of which are novel), and compare their performance on different benchmark problems. To appear in 18th International Conference on Theory and Applications of Satisfiability Testing, September 24-27, 2015, Austin, Texas, USA

Stable Model Counting and Its Application in Probabilistic Logic Programming

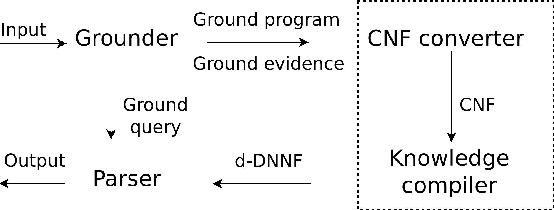
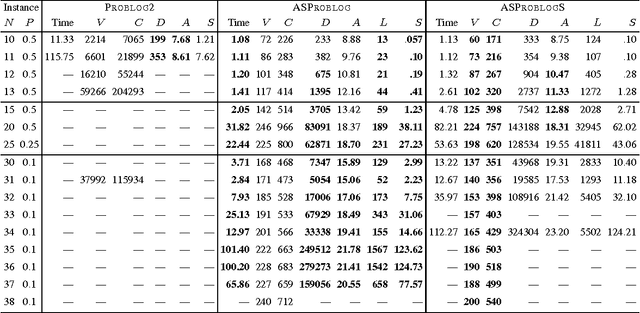
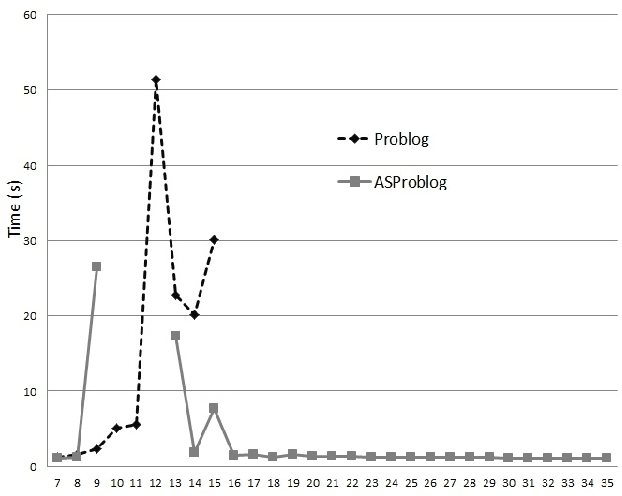
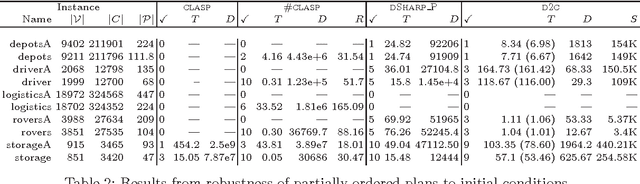
Model counting is the problem of computing the number of models that satisfy a given propositional theory. It has recently been applied to solving inference tasks in probabilistic logic programming, where the goal is to compute the probability of given queries being true provided a set of mutually independent random variables, a model (a logic program) and some evidence. The core of solving this inference task involves translating the logic program to a propositional theory and using a model counter. In this paper, we show that for some problems that involve inductive definitions like reachability in a graph, the translation of logic programs to SAT can be expensive for the purpose of solving inference tasks. For such problems, direct implementation of stable model semantics allows for more efficient solving. We present two implementation techniques, based on unfounded set detection, that extend a propositional model counter to a stable model counter. Our experiments show that for particular problems, our approach can outperform a state-of-the-art probabilistic logic programming solver by several orders of magnitude in terms of running time and space requirements, and can solve instances of significantly larger sizes on which the current solver runs out of time or memory.

Bound Founded Answer Set Programming

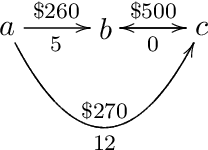
Answer Set Programming (ASP) is a powerful modelling formalism that is very efficient in solving combinatorial problems. ASP solvers implement the stable model semantics that eliminates circular derivations between Boolean variables from the solutions of a logic program. Due to this, ASP solvers are better suited than propositional satisfiability (SAT) and Constraint Programming (CP) solvers to solve a certain class of problems whose specification includes inductive definitions such as reachability in a graph. On the other hand, ASP solvers suffer from the grounding bottleneck that occurs due to their inability to model finite domain variables. Furthermore, the existing stable model semantics are not sufficient to disallow circular reasoning on the bounds of numeric variables. An example where this is required is in modelling shortest paths between nodes in a graph. Just as reachability can be encoded as an inductive definition with one or more base cases and recursive rules, shortest paths between nodes can also be modelled with similar base cases and recursive rules for their upper bounds. This deficiency of stable model semantics introduces another type of grounding bottleneck in ASP systems that cannot be removed by naively merging ASP with CP solvers, but requires a theoretical extension of the semantics from Booleans and normal rules to bounds over numeric variables and more general rules. In this work, we propose Bound Founded Answer Set Programming (BFASP) that resolves this issue and consequently, removes all types of grounding bottleneck inherent in ASP systems.

Grounding Bound Founded Answer Set Programs

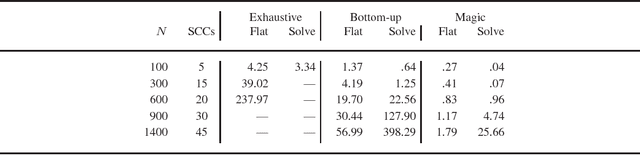
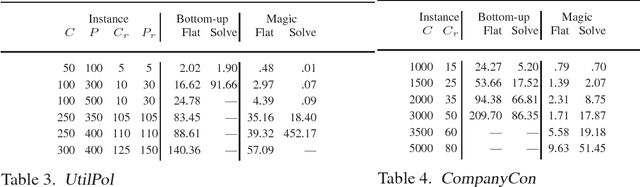
To appear in Theory and Practice of Logic Programming (TPLP) Bound Founded Answer Set Programming (BFASP) is an extension of Answer Set Programming (ASP) that extends stable model semantics to numeric variables. While the theory of BFASP is defined on ground rules, in practice BFASP programs are written as complex non-ground expressions. Flattening of BFASP is a technique used to simplify arbitrary expressions of the language to a small and well defined set of primitive expressions. In this paper, we first show how we can flatten arbitrary BFASP rule expressions, to give equivalent BFASP programs. Next, we extend the bottom-up grounding technique and magic set transformation used by ASP to BFASP programs. Our implementation shows that for BFASP problems, these techniques can significantly reduce the ground program size, and improve subsequent solving.