Grounding Bound Founded Answer Set Programs

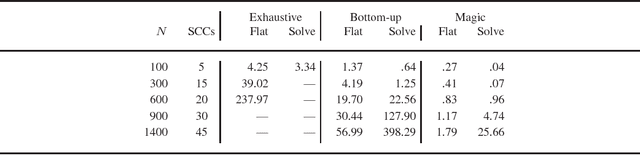
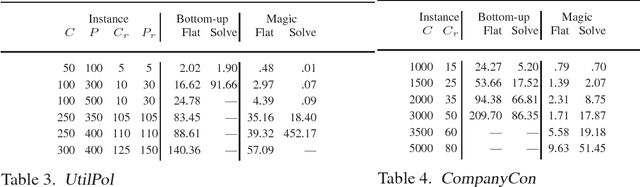
To appear in Theory and Practice of Logic Programming (TPLP) Bound Founded Answer Set Programming (BFASP) is an extension of Answer Set Programming (ASP) that extends stable model semantics to numeric variables. While the theory of BFASP is defined on ground rules, in practice BFASP programs are written as complex non-ground expressions. Flattening of BFASP is a technique used to simplify arbitrary expressions of the language to a small and well defined set of primitive expressions. In this paper, we first show how we can flatten arbitrary BFASP rule expressions, to give equivalent BFASP programs. Next, we extend the bottom-up grounding technique and magic set transformation used by ASP to BFASP programs. Our implementation shows that for BFASP problems, these techniques can significantly reduce the ground program size, and improve subsequent solving.

Boolean Equi-propagation for Concise and Efficient SAT Encodings of Combinatorial Problems

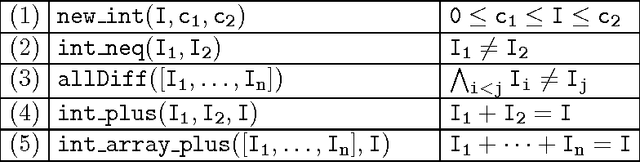
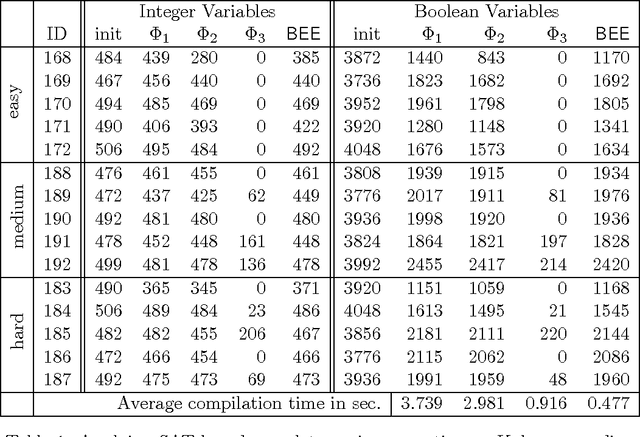
We present an approach to propagation-based SAT encoding of combinatorial problems, Boolean equi-propagation, where constraints are modeled as Boolean functions which propagate information about equalities between Boolean literals. This information is then applied to simplify the CNF encoding of the constraints. A key factor is that considering only a small fragment of a constraint model at one time enables us to apply stronger, and even complete, reasoning to detect equivalent literals in that fragment. Once detected, equivalences apply to simplify the entire constraint model and facilitate further reasoning on other fragments. Equi-propagation in combination with partial evaluation and constraint simplification provide the foundation for a powerful approach to SAT-based finite domain constraint solving. We introduce a tool called BEE (Ben-Gurion Equi-propagation Encoder) based on these ideas and demonstrate for a variety of benchmarks that our approach leads to a considerable reduction in the size of CNF encodings and subsequent speed-ups in SAT solving times.

Fast Set Bounds Propagation Using a BDD-SAT Hybrid

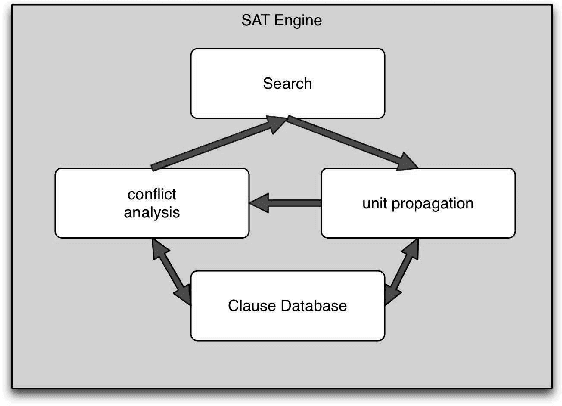
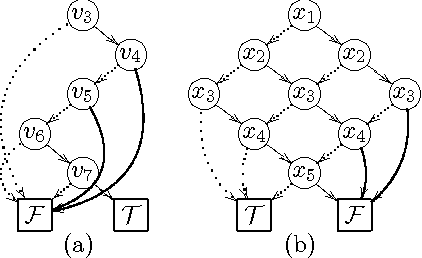
Binary Decision Diagram (BDD) based set bounds propagation is a powerful approach to solving set-constraint satisfaction problems. However, prior BDD based techniques in- cur the significant overhead of constructing and manipulating graphs during search. We present a set-constraint solver which combines BDD-based set-bounds propagators with the learning abilities of a modern SAT solver. Together with a number of improvements beyond the basic algorithm, this solver is highly competitive with existing propagation based set constraint solvers.