Breaking Symmetries in Graph Search with Canonizing Sets

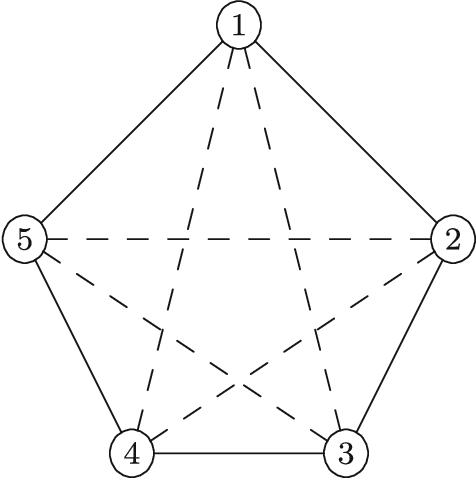
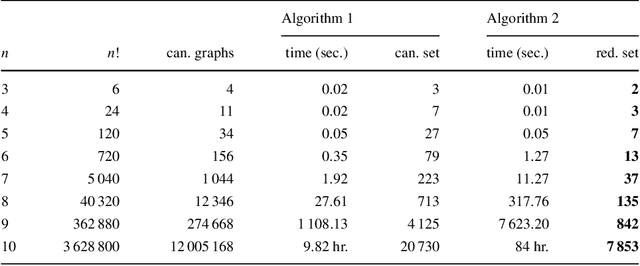
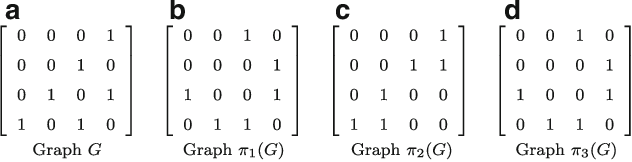
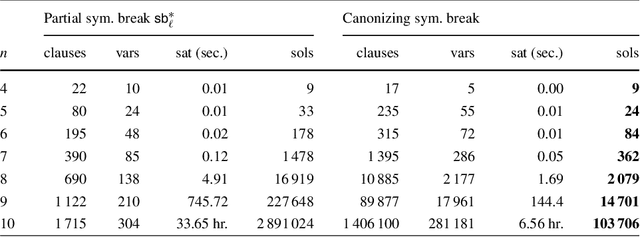
There are many complex combinatorial problems which involve searching for an undirected graph satisfying given constraints. Such problems are often highly challenging because of the large number of isomorphic representations of their solutions. This paper introduces effective and compact, complete symmetry breaking constraints for small graph search. Enumerating with these symmetry breaks generates all and only non-isomorphic solutions. For small search problems, with up to $10$ vertices, we compute instance independent symmetry breaking constraints. For small search problems with a larger number of vertices we demonstrate the computation of instance dependent constraints which are complete. We illustrate the application of complete symmetry breaking constraints to extend two known sequences from the OEIS related to graph enumeration. We also demonstrate the application of a generalization of our approach to fully-interchangeable matrix search problems.

Computing the Ramsey Number R(4,3,3) using Abstraction and Symmetry breaking

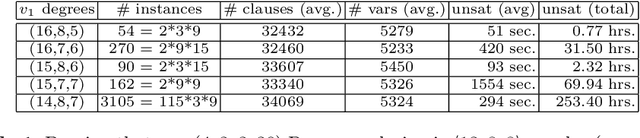
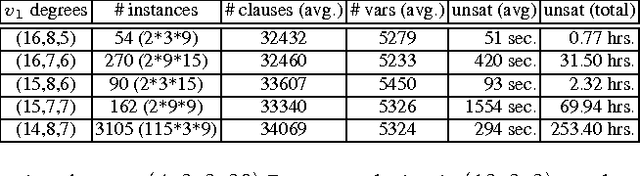
The number $R(4,3,3)$ is often presented as the unknown Ramsey number with the best chances of being found "soon". Yet, its precise value has remained unknown for almost 50 years. This paper presents a methodology based on \emph{abstraction} and \emph{symmetry breaking} that applies to solve hard graph edge-coloring problems. The utility of this methodology is demonstrated by using it to compute the value $R(4,3,3)=30$. Along the way it is required to first compute the previously unknown set ${\cal R}(3,3,3;13)$ consisting of 78{,}892 Ramsey colorings.

Solving Graph Coloring Problems with Abstraction and Symmetry

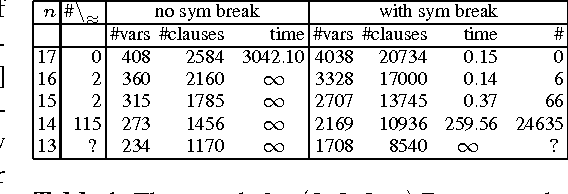
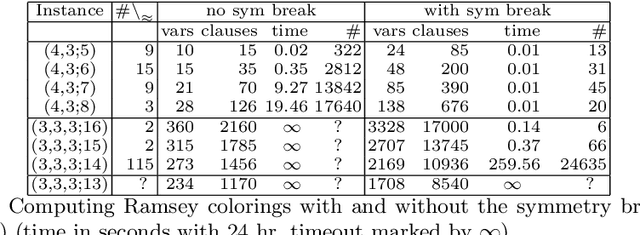
This paper introduces a general methodology, based on abstraction and symmetry, that applies to solve hard graph edge-coloring problems and demonstrates its use to provide further evidence that the Ramsey number $R(4,3,3)=30$. The number $R(4,3,3)$ is often presented as the unknown Ramsey number with the best chances of being found "soon". Yet, its precise value has remained unknown for more than 50 years. We illustrate our approach by showing that: (1) there are precisely 78{,}892 $(3,3,3;13)$ Ramsey colorings; and (2) if there exists a $(4,3,3;30)$ Ramsey coloring then it is (13,8,8) regular. Specifically each node has 13 edges in the first color, 8 in the second, and 8 in the third. We conjecture that these two results will help provide a proof that no $(4,3,3;30)$ Ramsey coloring exists implying that $R(4,3,3)=30$.

Boolean Equi-propagation for Concise and Efficient SAT Encodings of Combinatorial Problems

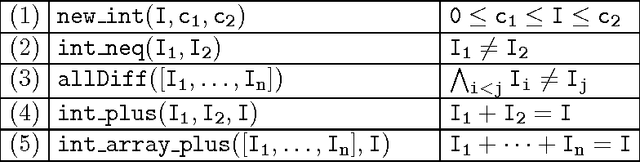
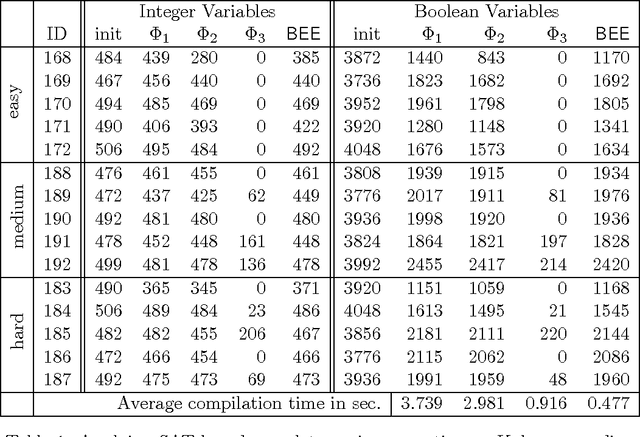
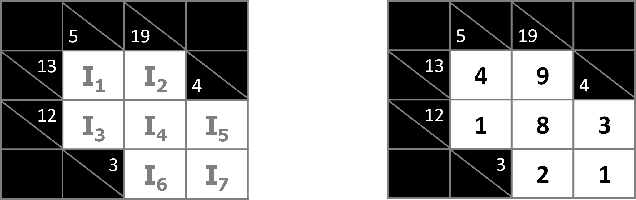
We present an approach to propagation-based SAT encoding of combinatorial problems, Boolean equi-propagation, where constraints are modeled as Boolean functions which propagate information about equalities between Boolean literals. This information is then applied to simplify the CNF encoding of the constraints. A key factor is that considering only a small fragment of a constraint model at one time enables us to apply stronger, and even complete, reasoning to detect equivalent literals in that fragment. Once detected, equivalences apply to simplify the entire constraint model and facilitate further reasoning on other fragments. Equi-propagation in combination with partial evaluation and constraint simplification provide the foundation for a powerful approach to SAT-based finite domain constraint solving. We introduce a tool called BEE (Ben-Gurion Equi-propagation Encoder) based on these ideas and demonstrate for a variety of benchmarks that our approach leads to a considerable reduction in the size of CNF encodings and subsequent speed-ups in SAT solving times.

Boolean Equi-propagation for Optimized SAT Encoding

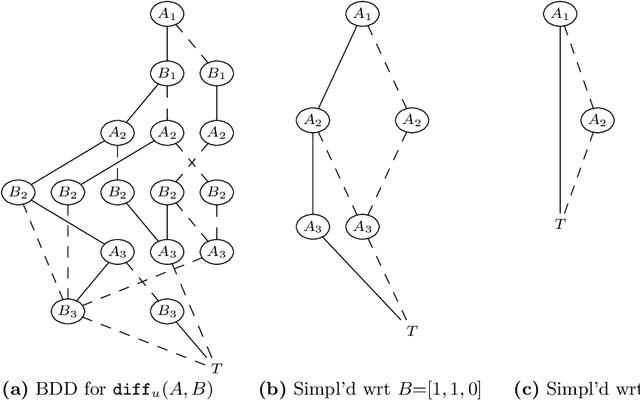
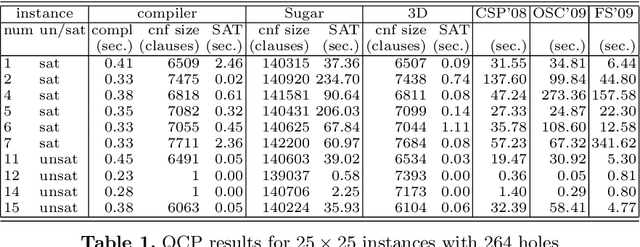
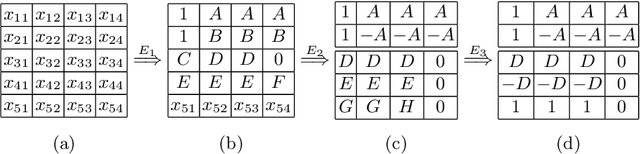
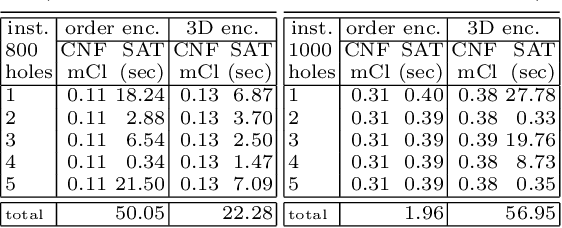
We present an approach to propagation based solving, Boolean equi-propagation, where constraints are modelled as propagators of information about equalities between Boolean literals. Propagation based solving applies this information as a form of partial evaluation resulting in optimized SAT encodings. We demonstrate for a variety of benchmarks that our approach results in smaller CNF encodings and leads to speed-ups in solving times.

Logic Programming with Satisfiability

This paper presents a Prolog interface to the MiniSat satisfiability solver. Logic program- ming with satisfiability combines the strengths of the two paradigms: logic programming for encoding search problems into satisfiability on the one hand and efficient SAT solving on the other. This synergy between these two exposes a programming paradigm which we propose here as a logic programming pearl. To illustrate logic programming with SAT solving we give an example Prolog program which solves instances of Partial MAXSAT.