Computing the Ramsey Number R(4,3,3) using Abstraction and Symmetry breaking
Paper and Code
Nov 01, 2015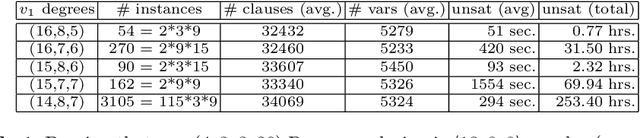

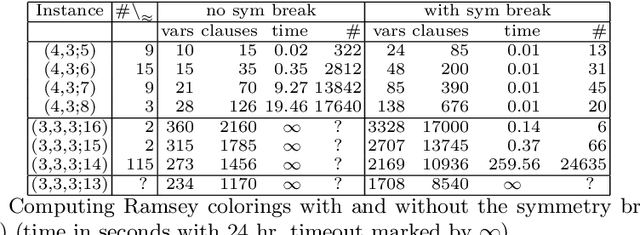

The number $R(4,3,3)$ is often presented as the unknown Ramsey number with the best chances of being found "soon". Yet, its precise value has remained unknown for almost 50 years. This paper presents a methodology based on \emph{abstraction} and \emph{symmetry breaking} that applies to solve hard graph edge-coloring problems. The utility of this methodology is demonstrated by using it to compute the value $R(4,3,3)=30$. Along the way it is required to first compute the previously unknown set ${\cal R}(3,3,3;13)$ consisting of 78{,}892 Ramsey colorings.
* arXiv admin note: text overlap with arXiv:1409.5189
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge