Breaking Symmetries in Graph Search with Canonizing Sets
Paper and Code
Feb 04, 2016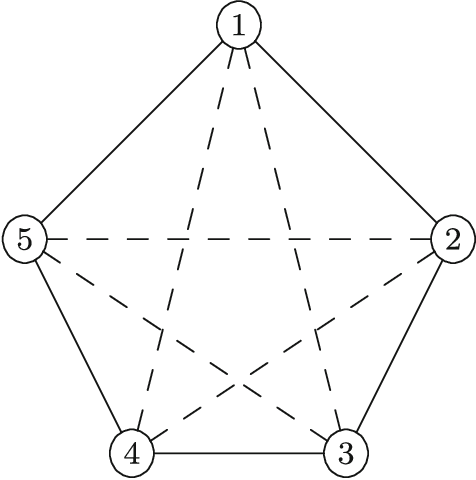
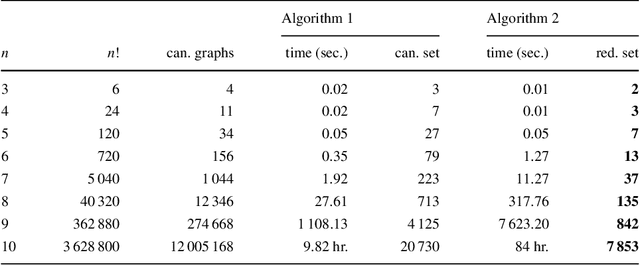
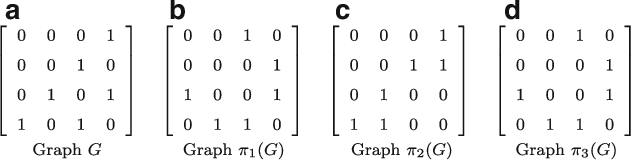
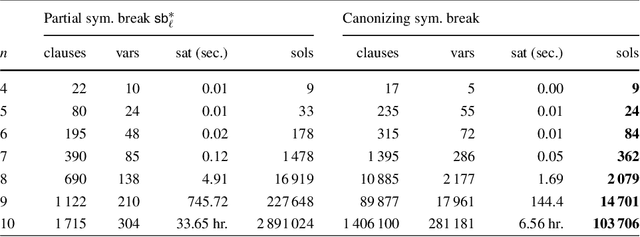
There are many complex combinatorial problems which involve searching for an undirected graph satisfying given constraints. Such problems are often highly challenging because of the large number of isomorphic representations of their solutions. This paper introduces effective and compact, complete symmetry breaking constraints for small graph search. Enumerating with these symmetry breaks generates all and only non-isomorphic solutions. For small search problems, with up to $10$ vertices, we compute instance independent symmetry breaking constraints. For small search problems with a larger number of vertices we demonstrate the computation of instance dependent constraints which are complete. We illustrate the application of complete symmetry breaking constraints to extend two known sequences from the OEIS related to graph enumeration. We also demonstrate the application of a generalization of our approach to fully-interchangeable matrix search problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge