Fast Set Bounds Propagation Using a BDD-SAT Hybrid

Binary Decision Diagram (BDD) based set bounds propagation is a powerful approach to solving set-constraint satisfaction problems. However, prior BDD based techniques in- cur the significant overhead of constructing and manipulating graphs during search. We present a set-constraint solver which combines BDD-based set-bounds propagators with the learning abilities of a modern SAT solver. Together with a number of improvements beyond the basic algorithm, this solver is highly competitive with existing propagation based set constraint solvers.

Boolean Equi-propagation for Optimized SAT Encoding

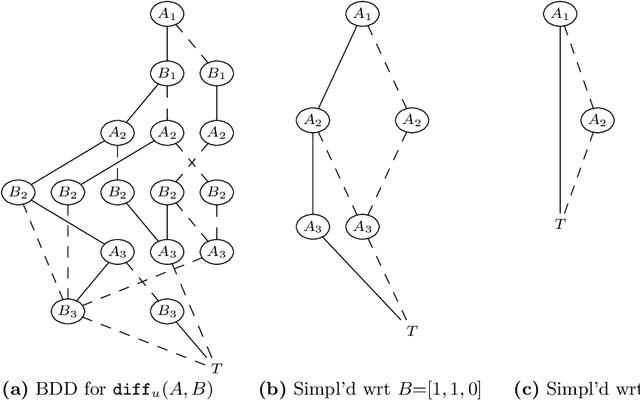
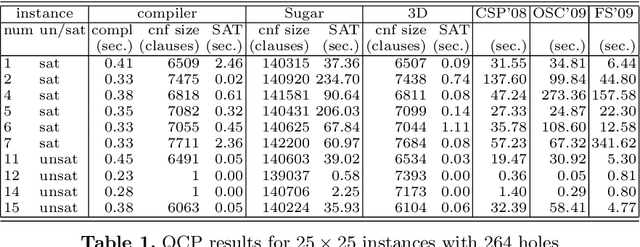
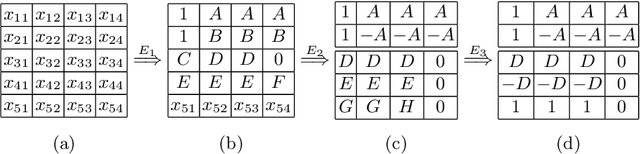
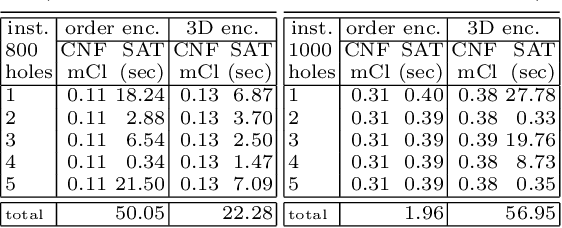
We present an approach to propagation based solving, Boolean equi-propagation, where constraints are modelled as propagators of information about equalities between Boolean literals. Propagation based solving applies this information as a form of partial evaluation resulting in optimized SAT encodings. We demonstrate for a variety of benchmarks that our approach results in smaller CNF encodings and leads to speed-ups in solving times.

Logic Programming with Satisfiability

This paper presents a Prolog interface to the MiniSat satisfiability solver. Logic program- ming with satisfiability combines the strengths of the two paradigms: logic programming for encoding search problems into satisfiability on the one hand and efficient SAT solving on the other. This synergy between these two exposes a programming paradigm which we propose here as a logic programming pearl. To illustrate logic programming with SAT solving we give an example Prolog program which solves instances of Partial MAXSAT.