Temporal Planning via Interval Logic Satisfiability for Autonomous Systems

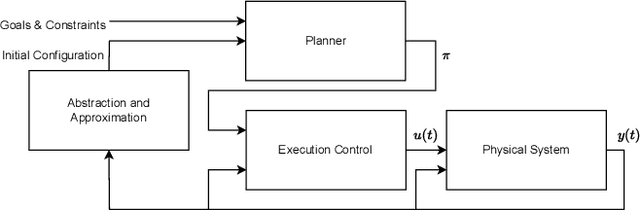
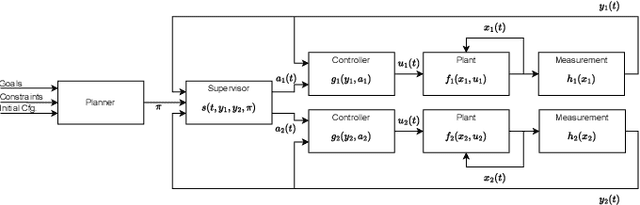
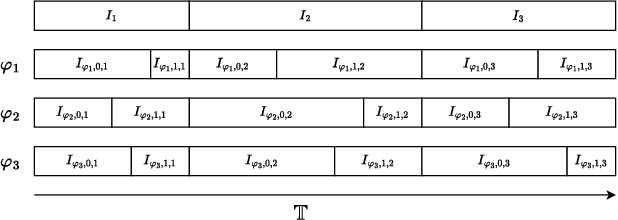
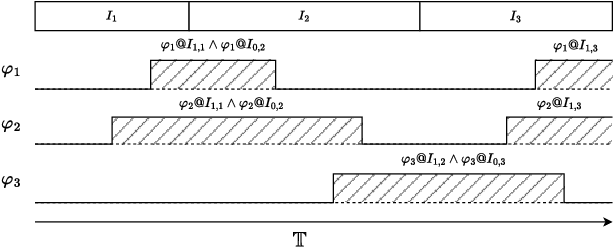
Many automated planning methods and formulations rely on suitably designed abstractions or simplifications of the constrained dynamics associated with agents to attain computational scalability. We consider formulations of temporal planning where intervals are associated with both action and fluent atoms, and relations between these are given as sentences in Allen's Interval Logic. We propose a notion of planning graphs that can account for complex concurrency relations between actions and fluents as a Constraint Programming (CP) model. We test an implementation of our algorithm on a state-of-the-art framework for CP and compare it with PDDL 2.1 planners that capture plans requiring complex concurrent interactions between agents. We demonstrate our algorithm outperforms existing PDDL 2.1 planners in the case studies. Still, scalability remains challenging when plans must comply with intricate concurrent interactions and the sequencing of actions.

Lifted Sequential Planning with Lazy Constraint Generation Solvers

This paper studies the possibilities made open by the use of Lazy Clause Generation (LCG) based approaches to Constraint Programming (CP) for tackling sequential classical planning. We propose a novel CP model based on seminal ideas on so-called lifted causal encodings for planning as satisfiability, that does not require grounding, as choosing groundings for functions and action schemas becomes an integral part of the problem of designing valid plans. This encoding does not require encoding frame axioms, and does not explicitly represent states as decision variables for every plan step. We also present a propagator procedure that illustrates the possibilities of LCG to widen the kind of inference methods considered to be feasible in planning as (iterated) CSP solving. We test encodings and propagators over classic IPC and recently proposed benchmarks for lifted planning, and report that for planning problem instances requiring fewer plan steps our methods compare very well with the state-of-the-art in optimal sequential planning.

Approximate Novelty Search

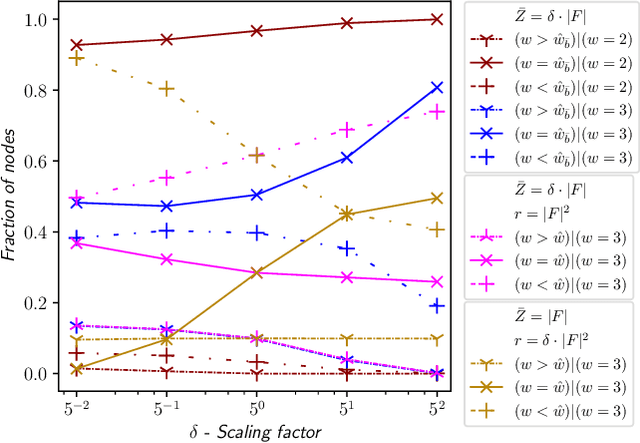
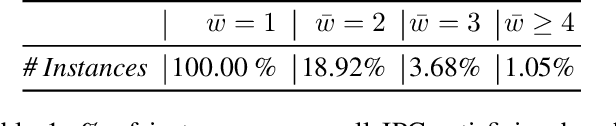
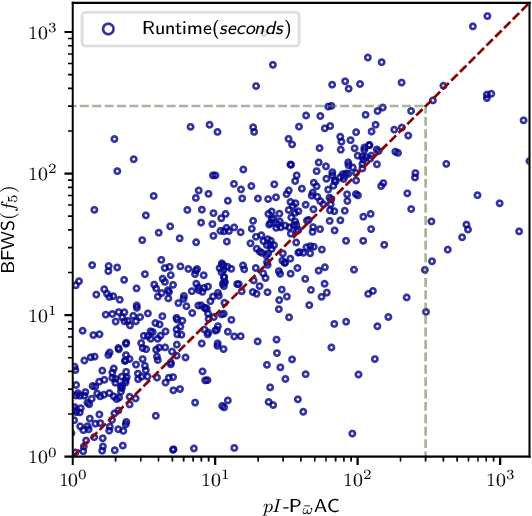
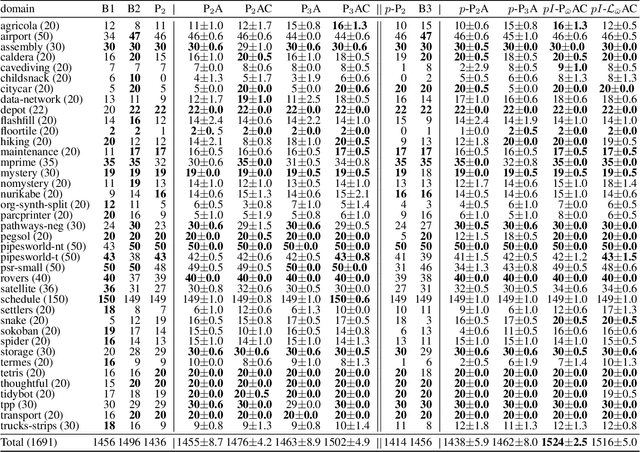
Width-based search algorithms seek plans by prioritizing states according to a suitably defined measure of novelty, that maps states into a set of novelty categories. Space and time complexity to evaluate state novelty is known to be exponential on the cardinality of the set. We present novel methods to obtain polynomial approximations of novelty and width-based search. First, we approximate novelty computation via random sampling and Bloom filters, reducing the runtime and memory footprint. Second, we approximate the best-first search using an adaptive policy that decides whether to forgo the expansion of nodes in the open list. These two techniques are integrated into existing width-based algorithms, resulting in new planners that perform significantly better than other state-of-the-art planners over benchmarks from the International Planning Competitions.