Temporal Planning via Interval Logic Satisfiability for Autonomous Systems
Paper and Code
Jun 14, 2024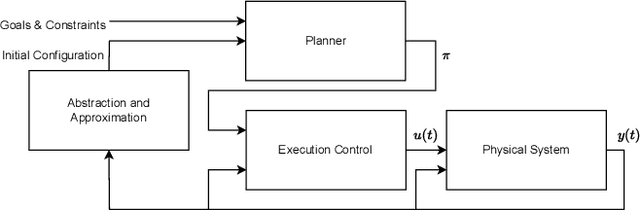
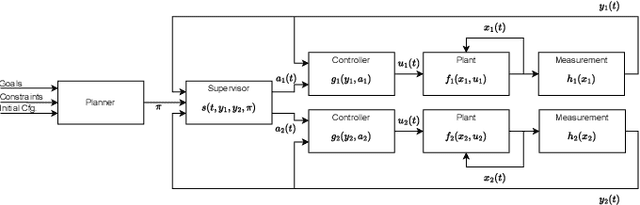
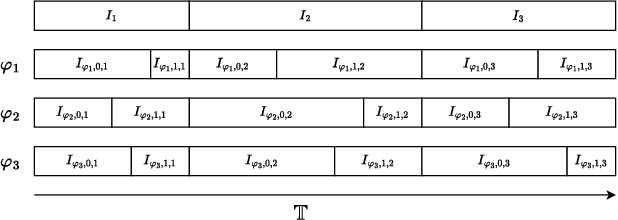
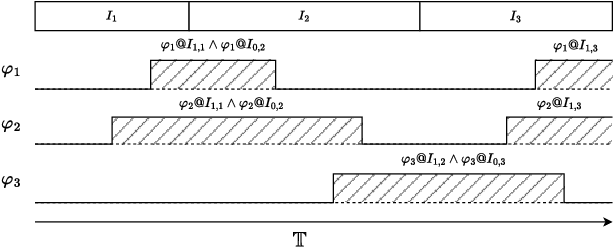
Many automated planning methods and formulations rely on suitably designed abstractions or simplifications of the constrained dynamics associated with agents to attain computational scalability. We consider formulations of temporal planning where intervals are associated with both action and fluent atoms, and relations between these are given as sentences in Allen's Interval Logic. We propose a notion of planning graphs that can account for complex concurrency relations between actions and fluents as a Constraint Programming (CP) model. We test an implementation of our algorithm on a state-of-the-art framework for CP and compare it with PDDL 2.1 planners that capture plans requiring complex concurrent interactions between agents. We demonstrate our algorithm outperforms existing PDDL 2.1 planners in the case studies. Still, scalability remains challenging when plans must comply with intricate concurrent interactions and the sequencing of actions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge