Parallel Strategies for Best-First Generalized Planning

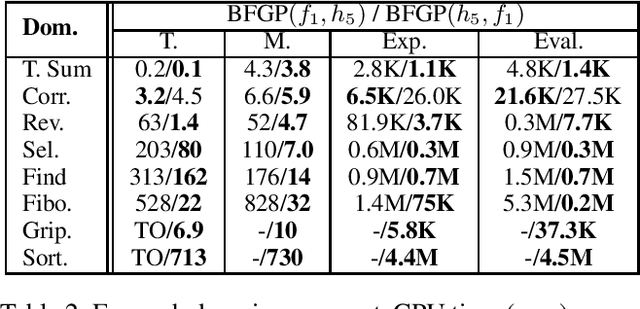
In recent years, there has been renewed interest in closing the performance gap between state-of-the-art planning solvers and generalized planning (GP), a research area of AI that studies the automated synthesis of algorithmic-like solutions capable of solving multiple classical planning instances. One of the current advancements has been the introduction of Best-First Generalized Planning (BFGP), a GP algorithm based on a novel solution space that can be explored with heuristic search, one of the foundations of modern planners. This paper evaluates the application of parallel search techniques to BFGP, another critical component in closing the performance gap. We first discuss why BFGP is well suited for parallelization and some of its differentiating characteristics from classical planners. Then, we propose two simple shared-memory parallel strategies with good scaling with the number of cores.

Synthesis of Procedural Models for Deterministic Transition Systems

This paper introduces a general approach for synthesizing procedural models of the state-transitions of a given discrete system. The approach is general in that it accepts different target languages for modeling the state-transitions of a discrete system; different model acquisition tasks with different target languages, such as the synthesis of STRIPS action models, or the update rule of a cellular automaton, fit as particular instances of our general approach. We follow an inductive approach to synthesis meaning that a set of examples of state-transitions, represented as (pre-state, action, post-state) tuples, are given as input. The goal is to synthesize a structured program that, when executed on a given pre-state, outputs its associated post-state. Our synthesis method implements a combinatorial search in the space of well-structured terminating programs that can be built using a Random-Access Machine (RAM), with a minimalist instruction set, and a finite amount of memory. The combinatorial search is guided with functions that asses the complexity of the candidate programs, as well as their fitness to the given input set of examples.

Generalized Planning as Heuristic Search: A new planning search-space that leverages pointers over objects

Planning as heuristic search is one of the most successful approaches to classical planning but unfortunately, it does not extend trivially to Generalized Planning (GP). GP aims to compute algorithmic solutions that are valid for a set of classical planning instances from a given domain, even if these instances differ in the number of objects, the number of state variables, their domain size, or their initial and goal configuration. The generalization requirements of GP make it impractical to perform the state-space search that is usually implemented by heuristic planners. This paper adapts the planning as heuristic search paradigm to the generalization requirements of GP, and presents the first native heuristic search approach to GP. First, the paper introduces a new pointer-based solution space for GP that is independent of the number of classical planning instances in a GP problem and the size of those instances (i.e. the number of objects, state variables and their domain sizes). Second, the paper defines a set of evaluation and heuristic functions for guiding a combinatorial search in our new GP solution space. The computation of these evaluation and heuristic functions does not require grounding states or actions in advance. Therefore our GP as heuristic search approach can handle large sets of state variables with large numerical domains, e.g.~integers. Lastly, the paper defines an upgraded version of our novel algorithm for GP called Best-First Generalized Planning (BFGP), that implements a best-first search in our pointer-based solution space, and that is guided by our evaluation/heuristic functions for GP.

Representation and Synthesis of C++ Programs for Generalized Planning

The paper introduces a novel representation for Generalized Planning (GP) problems, and their solutions, as C++ programs. Our C++ representation allows to formally proving the termination of generalized plans, and to specifying their asymptotic complexity w.r.t. the number of world objects. Characterizing the complexity of C++ generalized plans enables the application of a combinatorial search that enumerates the space of possible GP solutions in order of complexity. Experimental results show that our implementation of this approach, which we call BFGP++, outperforms the previous GP as heuristic search approach for the computation of generalized plans represented as compiler-styled programs. Last but not least, the execution of a C++ program on a classical planning instance is a deterministic grounding-free and search-free process, so our C++ representation allows us to automatically validate the computed solutions on large test instances of thousands of objects, where off-the-shelf classical planners get stuck either in the pre-processing or in the search.

Computing Programs for Generalized Planning as Heuristic Search

Although heuristic search is one of the most successful approaches to classical planning, this planning paradigm does not apply straightforwardly to Generalized Planning (GP). This paper adapts the planning as heuristic search paradigm to the particularities of GP, and presents the first native heuristic search approach to GP. First, the paper defines a program-based solution space for GP that is independent of the number of planning instances in a GP problem, and the size of these instances. Second, the paper defines the BFGP algorithm for GP, that implements a best-first search in our program-based solution space, and that is guided by different evaluation and heuristic functions.

Scaling-up Generalized Planning as Heuristic Search with Landmarks

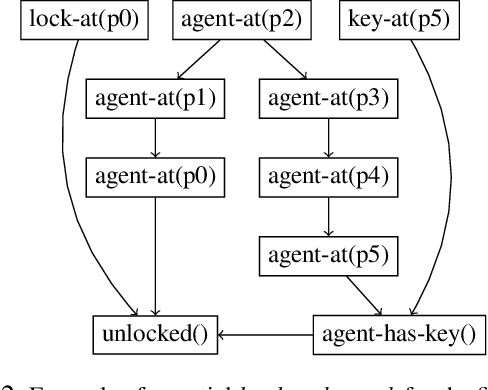
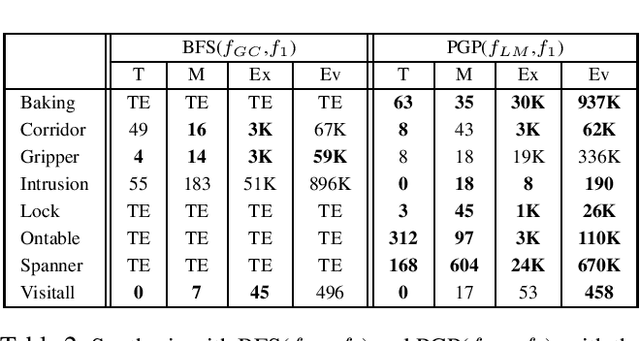
Landmarks are one of the most effective search heuristics for classical planning, but largely ignored in generalized planning. Generalized planning (GP) is usually addressed as a combinatorial search in a given space of algorithmic solutions, where candidate solutions are evaluated w.r.t.~the instances they solve. This type of solution evaluation ignores any sub-goal information that is not explicit in the representation of the planning instances, causing plateaus in the space of candidate generalized plans. Furthermore, node expansion in GP is a run-time bottleneck since it requires evaluating every child node over the entire batch of classical planning instances in a GP problem. In this paper we define a landmark counting heuristic for GP (that considers sub-goal information that is not explicitly represented in the planning instances), and a novel heuristic search algorithm for GP (that we call PGP) and that progressively processes subsets of the planning instances of a GP problem. Our two orthogonal contributions are analyzed in an ablation study, showing that both improve the state-of-the-art in GP as heuristic search, and that both benefit from each other when used in combination.

Approximate Novelty Search

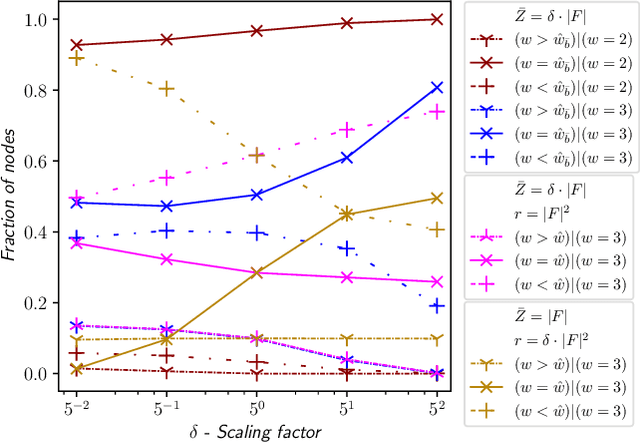
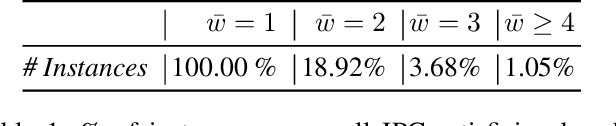
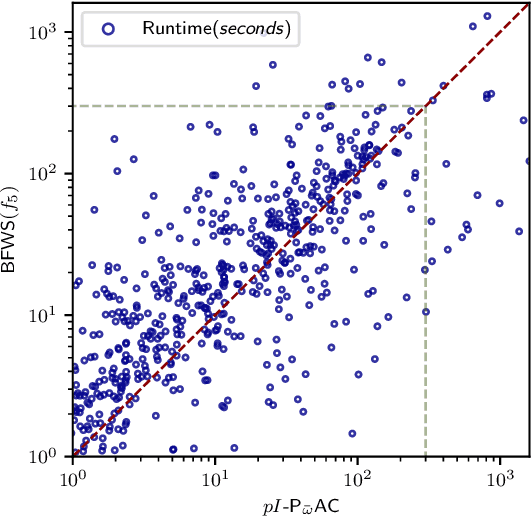
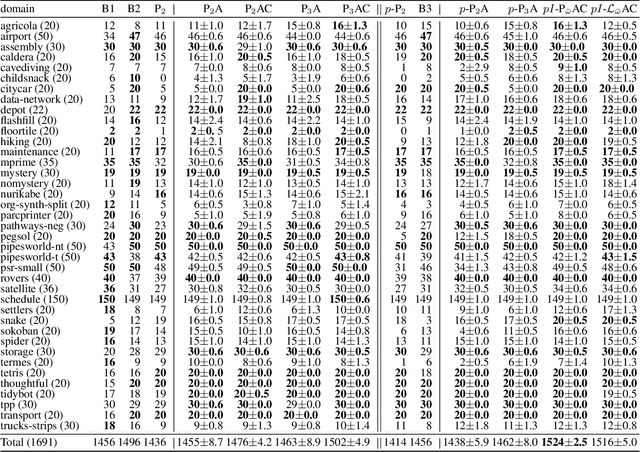
Width-based search algorithms seek plans by prioritizing states according to a suitably defined measure of novelty, that maps states into a set of novelty categories. Space and time complexity to evaluate state novelty is known to be exponential on the cardinality of the set. We present novel methods to obtain polynomial approximations of novelty and width-based search. First, we approximate novelty computation via random sampling and Bloom filters, reducing the runtime and memory footprint. Second, we approximate the best-first search using an adaptive policy that decides whether to forgo the expansion of nodes in the open list. These two techniques are integrated into existing width-based algorithms, resulting in new planners that perform significantly better than other state-of-the-art planners over benchmarks from the International Planning Competitions.

Generalized Planning as Heuristic Search

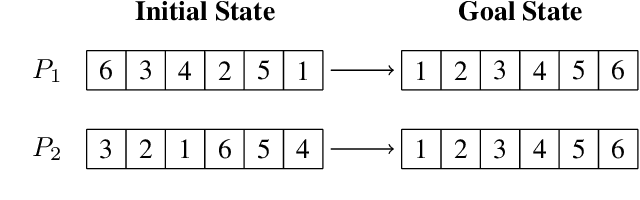
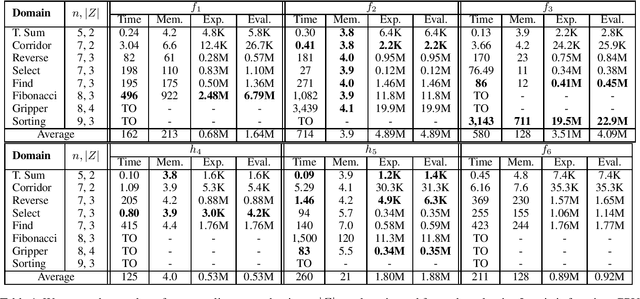
Although heuristic search is one of the most successful approaches to classical planning, this planning paradigm does not apply straightforwardly to Generalized Planning (GP). Planning as heuristic search traditionally addresses the computation of sequential plans by searching in a grounded state-space. On the other hand GP aims at computing algorithm-like plans, that can branch and loop, and that generalize to a (possibly infinite) set of classical planning instances. This paper adapts the planning as heuristic search paradigm to the particularities of GP, and presents the first native heuristic search approach to GP. First, the paper defines a novel GP solution space that is independent of the number of planning instances in a GP problem, and the size of these instances. Second, the paper defines different evaluation and heuristic functions for guiding a combinatorial search in our GP solution space. Lastly the paper defines a GP algorithm, called Best-First Generalized Planning (BFGP), that implements a best-first search in the solution space guided by our evaluation/heuristic functions.

Online Action Recognition

Recognition in planning seeks to find agent intentions, goals or activities given a set of observations and a knowledge library (e.g. goal states, plans or domain theories). In this work we introduce the problem of Online Action Recognition. It consists in recognizing, in an open world, the planning action that best explains a partially observable state transition from a knowledge library of first-order STRIPS actions, which is initially empty. We frame this as an optimization problem, and propose two algorithms to address it: Action Unification (AU) and Online Action Recognition through Unification (OARU). The former builds on logic unification and generalizes two input actions using weighted partial MaxSAT. The latter looks for an action within the library that explains an observed transition. If there is such action, it generalizes it making use of AU, building in this way an AU hierarchy. Otherwise, OARU inserts a Trivial Grounded Action (TGA) in the library that explains just that transition. We report results on benchmarks from the International Planning Competition and PDDLGym, where OARU recognizes actions accurately with respect to expert knowledge, and shows real-time performance.

Leveraging Multiple Environments for Learning and Decision Making: a Dismantling Use Case

Learning is usually performed by observing real robot executions. Physics-based simulators are a good alternative for providing highly valuable information while avoiding costly and potentially destructive robot executions. We present a novel approach for learning the probabilities of symbolic robot action outcomes. This is done leveraging different environments, such as physics-based simulators, in execution time. To this end, we propose MENID (Multiple Environment Noise Indeterministic Deictic) rules, a novel representation able to cope with the inherent uncertainties present in robotic tasks. MENID rules explicitly represent each possible outcomes of an action, keep memory of the source of the experience, and maintain the probability of success of each outcome. We also introduce an algorithm to distribute actions among environments, based on previous experiences and expected gain. Before using physics-based simulations, we propose a methodology for evaluating different simulation settings and determining the least time-consuming model that could be used while still producing coherent results. We demonstrate the validity of the approach in a dismantling use case, using a simulation with reduced quality as simulated system, and a simulation with full resolution where we add noise to the trajectories and some physical parameters as a representation of the real system.