Learning The Minimum Action Distance

This paper presents a state representation framework for Markov decision processes (MDPs) that can be learned solely from state trajectories, requiring neither reward signals nor the actions executed by the agent. We propose learning the minimum action distance (MAD), defined as the minimum number of actions required to transition between states, as a fundamental metric that captures the underlying structure of an environment. MAD naturally enables critical downstream tasks such as goal-conditioned reinforcement learning and reward shaping by providing a dense, geometrically meaningful measure of progress. Our self-supervised learning approach constructs an embedding space where the distances between embedded state pairs correspond to their MAD, accommodating both symmetric and asymmetric approximations. We evaluate the framework on a comprehensive suite of environments with known MAD values, encompassing both deterministic and stochastic dynamics, as well as discrete and continuous state spaces, and environments with noisy observations. Empirical results demonstrate that the proposed approach not only efficiently learns accurate MAD representations across these diverse settings but also significantly outperforms existing state representation methods in terms of representation quality.

Distances for Markov chains from sample streams

Bisimulation metrics are powerful tools for measuring similarities between stochastic processes, and specifically Markov chains. Recent advances have uncovered that bisimulation metrics are, in fact, optimal-transport distances, which has enabled the development of fast algorithms for computing such metrics with provable accuracy and runtime guarantees. However, these recent methods, as well as all previously known methods, assume full knowledge of the transition dynamics. This is often an impractical assumption in most real-world scenarios, where typically only sample trajectories are available. In this work, we propose a stochastic optimization method that addresses this limitation and estimates bisimulation metrics based on sample access, without requiring explicit transition models. Our approach is derived from a new linear programming (LP) formulation of bisimulation metrics, which we solve using a stochastic primal-dual optimization method. We provide theoretical guarantees on the sample complexity of the algorithm and validate its effectiveness through a series of empirical evaluations.

Provably Efficient Exploration in Reward Machines with Low Regret

We study reinforcement learning (RL) for decision processes with non-Markovian reward, in which high-level knowledge of the task in the form of reward machines is available to the learner. We consider probabilistic reward machines with initially unknown dynamics, and investigate RL under the average-reward criterion, where the learning performance is assessed through the notion of regret. Our main algorithmic contribution is a model-based RL algorithm for decision processes involving probabilistic reward machines that is capable of exploiting the structure induced by such machines. We further derive high-probability and non-asymptotic bounds on its regret and demonstrate the gain in terms of regret over existing algorithms that could be applied, but obliviously to the structure. We also present a regret lower bound for the studied setting. To the best of our knowledge, the proposed algorithm constitutes the first attempt to tailor and analyze regret specifically for RL with probabilistic reward machines.

Tractable Offline Learning of Regular Decision Processes

This work studies offline Reinforcement Learning (RL) in a class of non-Markovian environments called Regular Decision Processes (RDPs). In RDPs, the unknown dependency of future observations and rewards from the past interactions can be captured by some hidden finite-state automaton. For this reason, many RDP algorithms first reconstruct this unknown dependency using automata learning techniques. In this paper, we show that it is possible to overcome two strong limitations of previous offline RL algorithms for RDPs, notably RegORL. This can be accomplished via the introduction of two original techniques: the development of a new pseudometric based on formal languages, which removes a problematic dependency on $L_\infty^\mathsf{p}$-distinguishability parameters, and the adoption of Count-Min-Sketch (CMS), instead of naive counting. The former reduces the number of samples required in environments that are characterized by a low complexity in language-theoretic terms. The latter alleviates the memory requirements for long planning horizons. We derive the PAC sample complexity bounds associated to each of these techniques, and we validate the approach experimentally.

Hierarchical Average-Reward Linearly-solvable Markov Decision Processes

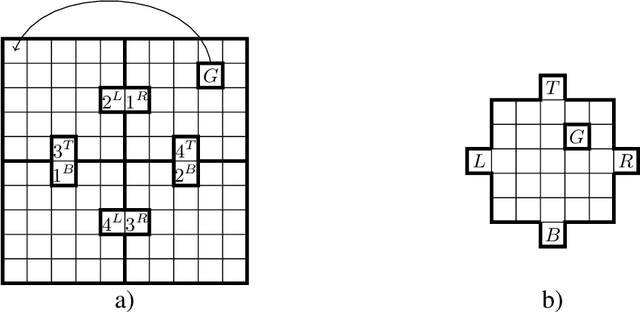
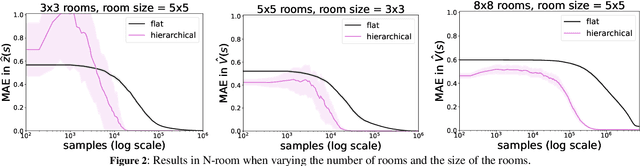
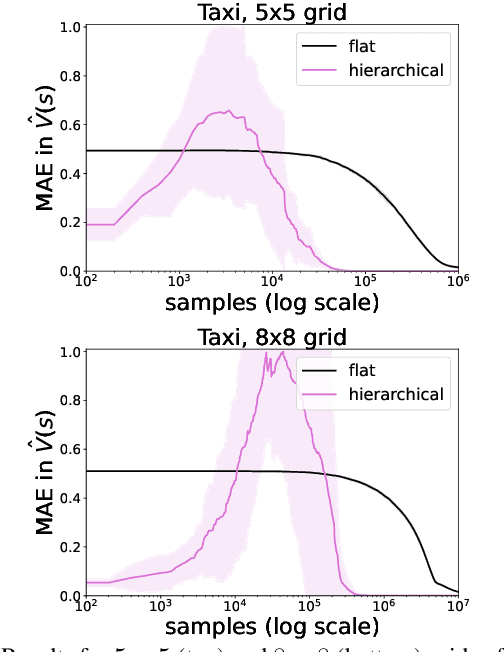
We introduce a novel approach to hierarchical reinforcement learning for Linearly-solvable Markov Decision Processes (LMDPs) in the infinite-horizon average-reward setting. Unlike previous work, our approach allows learning low-level and high-level tasks simultaneously, without imposing limiting restrictions on the low-level tasks. Our method relies on partitions of the state space that create smaller subtasks that are easier to solve, and the equivalence between such partitions to learn more efficiently. We then exploit the compositionality of low-level tasks to exactly represent the value function of the high-level task. Experiments show that our approach can outperform flat average-reward reinforcement learning by one or several orders of magnitude.

Bisimulation Metrics are Optimal Transport Distances, and Can be Computed Efficiently

We propose a new framework for formulating optimal transport distances between Markov chains. Previously known formulations studied couplings between the entire joint distribution induced by the chains, and derived solutions via a reduction to dynamic programming (DP) in an appropriately defined Markov decision process. This formulation has, however, not led to particularly efficient algorithms so far, since computing the associated DP operators requires fully solving a static optimal transport problem, and these operators need to be applied numerous times during the overall optimization process. In this work, we develop an alternative perspective by considering couplings between a flattened version of the joint distributions that we call discounted occupancy couplings, and show that calculating optimal transport distances in the full space of joint distributions can be equivalently formulated as solving a linear program (LP) in this reduced space. This LP formulation allows us to port several algorithmic ideas from other areas of optimal transport theory. In particular, our formulation makes it possible to introduce an appropriate notion of entropy regularization into the optimization problem, which in turn enables us to directly calculate optimal transport distances via a Sinkhorn-like method we call Sinkhorn Value Iteration (SVI). We show both theoretically and empirically that this method converges quickly to an optimal coupling, essentially at the same computational cost of running vanilla Sinkhorn in each pair of states. Along the way, we point out that our optimal transport distance exactly matches the common notion of bisimulation metrics between Markov chains, and thus our results also apply to computing such metrics, and in fact our algorithm turns out to be significantly more efficient than the best known methods developed so far for this purpose.

Planning with a Learned Policy Basis to Optimally Solve Complex Tasks

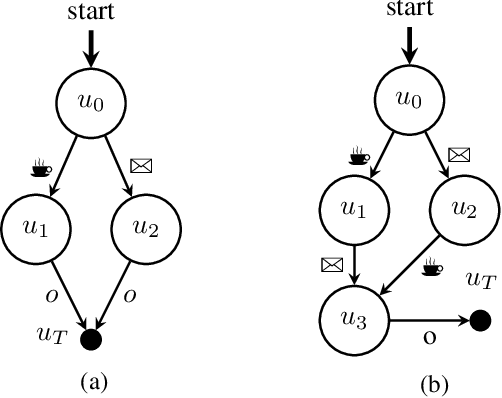
Conventional reinforcement learning (RL) methods can successfully solve a wide range of sequential decision problems. However, learning policies that can generalize predictably across multiple tasks in a setting with non-Markovian reward specifications is a challenging problem. We propose to use successor features to learn a policy basis so that each (sub)policy in it solves a well-defined subproblem. In a task described by a finite state automaton (FSA) that involves the same set of subproblems, the combination of these (sub)policies can then be used to generate an optimal solution without additional learning. In contrast to other methods that combine (sub)policies via planning, our method asymptotically attains global optimality, even in stochastic environments.

Asymmetric Norms to Approximate the Minimum Action Distance

This paper presents a state representation for reward-free Markov decision processes. The idea is to learn, in a self-supervised manner, an embedding space where distances between pairs of embedded states correspond to the minimum number of actions needed to transition between them. Unlike previous methods, our approach incorporates an asymmetric norm parametrization, enabling accurate approximations of minimum action distances in environments with inherent asymmetry. We show how this representation can be leveraged to learn goal-conditioned policies, providing a notion of similarity between states and goals and a useful heuristic distance to guide planning. To validate our approach, we conduct empirical experiments on both symmetric and asymmetric environments. Our results show that our asymmetric norm parametrization performs comparably to symmetric norms in symmetric environments and surpasses symmetric norms in asymmetric environments.

Generalized Planning as Heuristic Search: A new planning search-space that leverages pointers over objects

Planning as heuristic search is one of the most successful approaches to classical planning but unfortunately, it does not extend trivially to Generalized Planning (GP). GP aims to compute algorithmic solutions that are valid for a set of classical planning instances from a given domain, even if these instances differ in the number of objects, the number of state variables, their domain size, or their initial and goal configuration. The generalization requirements of GP make it impractical to perform the state-space search that is usually implemented by heuristic planners. This paper adapts the planning as heuristic search paradigm to the generalization requirements of GP, and presents the first native heuristic search approach to GP. First, the paper introduces a new pointer-based solution space for GP that is independent of the number of classical planning instances in a GP problem and the size of those instances (i.e. the number of objects, state variables and their domain sizes). Second, the paper defines a set of evaluation and heuristic functions for guiding a combinatorial search in our new GP solution space. The computation of these evaluation and heuristic functions does not require grounding states or actions in advance. Therefore our GP as heuristic search approach can handle large sets of state variables with large numerical domains, e.g.~integers. Lastly, the paper defines an upgraded version of our novel algorithm for GP called Best-First Generalized Planning (BFGP), that implements a best-first search in our pointer-based solution space, and that is guided by our evaluation/heuristic functions for GP.

Hierarchies of Reward Machines

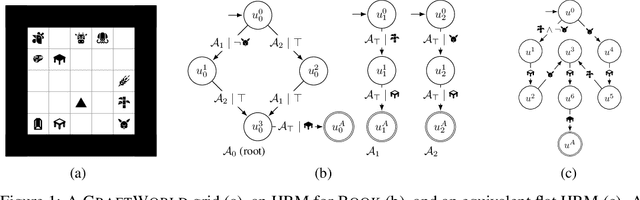
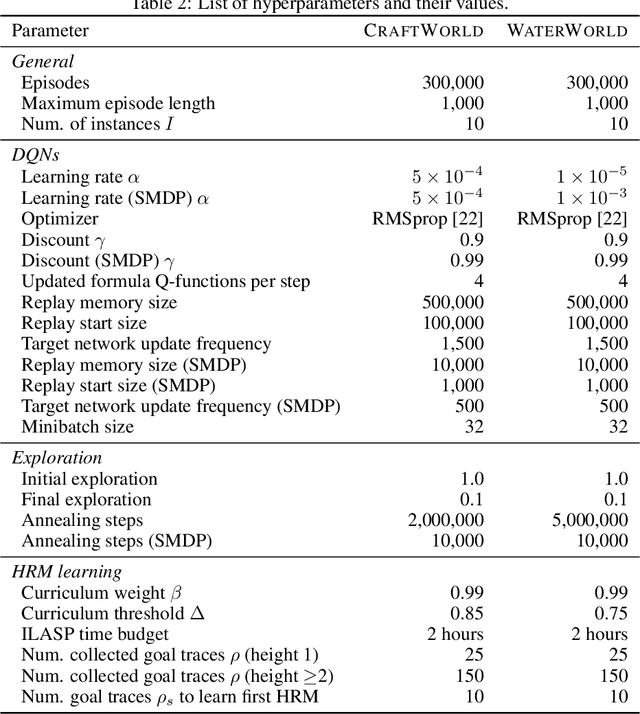
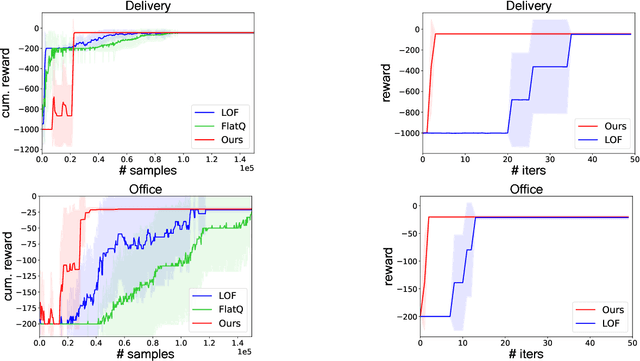
Reward machines (RMs) are a recent formalism for representing the reward function of a reinforcement learning task through a finite-state machine whose edges encode landmarks of the task using high-level events. The structure of RMs enables the decomposition of a task into simpler and independently solvable subtasks that help tackle long-horizon and/or sparse reward tasks. We propose a formalism for further abstracting the subtask structure by endowing an RM with the ability to call other RMs, thus composing a hierarchy of RMs (HRM). We exploit HRMs by treating each call to an RM as an independently solvable subtask using the options framework, and describe a curriculum-based method to induce HRMs from example traces observed by the agent. Our experiments reveal that exploiting a handcrafted HRM leads to faster convergence than with a flat HRM, and that learning an HRM is more scalable than learning an equivalent flat HRM.